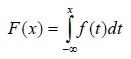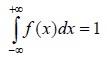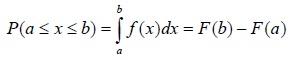- •1. Классификация случайных событий: возможные и невозможные события, совместные и несовместные, противоположные и достоверные события. Примеры.
- •2. Полная группа событий. Пространство элементарных исходов. Примеры.
- •3. Классическое определение вероятности события. Свойства вероятности события. Примеры.
- •4. Статистическое определение вероятности события. Примеры. Теорема Бернулли (с доказательством).
- •5. Геометрическое определение вероятности. Примеры.
- •6. Сумма событий и ее свойства. Примеры.
- •7. Теорема сложения вероятностей (с доказательством) и ее следствия. Примеры. 8 Произведение событий и его свойства.
- •9. Условная вероятность. Зависимые и независимые события. Теорема умножения вероятностей (с доказательством). Примеры
- •11. Случайная величина (определение). Дискретная случайная величина и ее закон (ряд) распределения. Основное свойство закона распределения. Примеры.
- •Определение независимости случайных величин.
- •13.* Математические операции над дискретными случайными величинами. Примеры.
- •14. Функция распределения случайной величины, ее определение, свойства и график. Примеры.
- •15. Функция распределения дискретной случайной величины. Примеры.
- •16. Теорема о существовании случайной величины с заданной функцией распределения. Непрерывная случайная величина. Вероятность отдельно взятого значения непрерывной случайной величины. Примеры.
- •18. Математическое ожидание случайной величины и его свойства. Примеры
- •Свойства математического ожидания
- •Доказательство:
- •19. Дисперсия случайной величины и ее свойства. Среднее квадратическое отклонение случайной величины. Примеры.
- •1. Дискретная случайная величина, закон и функция распределения
- •2. Числовые характеристики дискретных случайных величин
- •20. Закон распределения Бернулли, его определение, свойства и примеры.
- •21. Биномиальный закон распределения, его определение, свойства и примеры.
- •22.Закон распределения Пуассона, его определение, свойства и примеры.
- •25. Нормальный (гауссовский) закон распределения.
- •26. Стандартный нормальный закон распределения. Функция Гаусса, ее свойства и график. Теорема о связи плотности нормального закона распределения и функции Гаусса.
- •27. Функция Лапласа, ее свойства, график и геометрический смысл. Теорема о связи функции распределения нормального закона и функции Лапласа. Примеры.
- •28.* Свойства случайной величины, распределенной по нормальному закону. Правило трех сигм. Примеры.
- •29.* Показательный (экспоненциальный) закон распределения, его определение, свойства и примеры.
- •34. Лемма Чебышева. Примеры
- •35. Неравенство Чебышева. Примеры
- •36. Понятие двумерной (n-мерной) случайной величины. Примеры. Одномерные распределения ее составляющих. Условные распределения.
- •37. Ковариация и коэффициент корреляции случайных величин. Связь между некоррелированностью и независимостью случайных величин
14. Функция распределения случайной величины, ее определение, свойства и график. Примеры.
Числовая величина, принимающая то или иное значение в результате реализации испытания случайным образом, называется случайной величиной.
Если x - дискретная случайная величина, принимающая значения x1 < x2 < … < xi < … с вероятностями p1 < p2 < … < pi < …, то таблица вида
|
x1 |
x2 |
… |
xi |
… |
|
p1 |
p2 |
… |
pi |
… |
называется распределением дискретной случайной величины.
Функция распределения случайной величины, с таким распределением, имеет вид

Свойства функции распределения.
1.
 .
.
Доказательство: Это утверждение
следует из того, что функция распределения
– это вероятность, а как известно, .
.
2.Функция распределения случайной величины есть неубывающая функция на всей числовой оси.
Доказательство:Пусть х1<x2.
Докажем, чтоF(x1) F(x2).
Пусть событие А=(Х<x1),B=(x1
F(x2).
Пусть событие А=(Х<x1),B=(x1 Х<x2).
Тогда А+В=(Х<x2).
События А и В несовместны, следовательно
по теореме сложения Р(А+В)=P(А)+P(В).
То есть Р(Х<x2)
=Р(Х<x1)+Р(x1
Х<x2).
Тогда А+В=(Х<x2).
События А и В несовместны, следовательно
по теореме сложения Р(А+В)=P(А)+P(В).
То есть Р(Х<x2)
=Р(Х<x1)+Р(x1 Х<x2).
Другими словамиF(x2)=F(x1)+
Р(x1
Х<x2).
Другими словамиF(x2)=F(x1)+
Р(x1 Х<x2).(3)
Х<x2).(3)
Так как Р(x1 Х<x2)
Х<x2)
 как вероятность невозможного события
Х
как вероятность невозможного события
Х .
.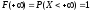 как вероятность достовероного события
Х
как вероятность достовероного события
Х .
.
4.
Р(х1 Х<x2)=F(x2)-F(x1).(4)
Х<x2)=F(x2)-F(x1).(4)
Доказательство: это непосредственно
следует из формулы (3). 
Пример:
 Найти вероятность того, что случайная
величина Х примет значение в интервале
[2; 5).
Найти вероятность того, что случайная
величина Х примет значение в интервале
[2; 5).
Решение: По формуле Р(х1 Х<x2)=F(x2)-F(x1).(4)
Х<x2)=F(x2)-F(x1).(4)
Р(2 Х<5)=F(5)-F(2)=1-2/3=1/3.(4).
Х<5)=F(5)-F(2)=1-2/3=1/3.(4).
Ответ :1/3.
15. Функция распределения дискретной случайной величины. Примеры.
если - дискретная случайная величина, принимающая значения x1 < x2 < … < xi < … с вероятностями p1 < p2 < … < pi < …, то таблица вида
|
x1 |
x2 |
… |
xi |
… |
|
p1 |
p2 |
… |
pi |
… |
называется распределением дискретной случайной величины.
Функция распределения случайной величины, с таким распределением, имеет вид

У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |


16. Теорема о существовании случайной величины с заданной функцией распределения. Непрерывная случайная величина. Вероятность отдельно взятого значения непрерывной случайной величины. Примеры.
Как известно, случайной величиной называется переменная величина, которая может принимать те или иные значения в зависимости от случая. Случайные величины обозначают заглавными буквами латинского алфавита (X, Y, Z), а их значения – соответствующими строчными буквами (x, y, z). различают непрерывные и дискретные случайные величины.
Непрерывной случайной величиной называется случайная величина Х, если ее функция распределения (интегральная функция распределения) представима в виде:
|
|
где f(x) – некоторая неотрицательная функция, такая что
|
|
Функция f(x) называется плотностью распределения вероятностей случайной величины X (дифференциальной функцией распределения).
Вероятность того, что непрерывная случайная величина X принимает значение в заданном промежутке, вычисляется следующим образом:
|
|
Примеры распределений вероятностей непрерывной случайной величины Х:
равномерное распределение вероятностей непрерывной случайной величины;
показательное распределение вероятностей непрерывной случайной величины;
нормальное распределение вероятностей непрерывной случайной величины.
17. Абсолютно непрерывная случайная величина. Плотность вероятности абсолютно непрерывной случайной величины, ее определение, свойства, и график.
Важный класс непрерывных случайных величин -- абсолютно непрерывные случайные величины. Это случайные величины, распределение которых имеет плотность.
Определение 3.7
Случайная величина ![]() называетсяабсолютно
непрерывной, если
существует функция
называетсяабсолютно
непрерывной, если
существует функция ![]() такая,
что
такая,
что
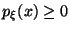 ,
, ,
,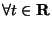 имеет
место равенство:
имеет
место равенство: 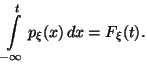
Функция ![]() ,
обладающая вышеперечисленными свойствами,
называетсяплотностью
распределения случайной величины
,
обладающая вышеперечисленными свойствами,
называетсяплотностью
распределения случайной величины ![]() .
.
Следствие 3.1
Если ![]() --
абсолютно непрерывная случайная
величина, то
--
абсолютно непрерывная случайная
величина, то

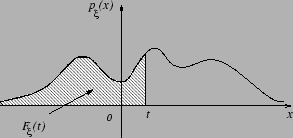
Наглядный смысл плотности можно проиллюстрировать следующим рисунком.

Замечание 3.5
Если плотность ![]() непрерывна
в точке
непрерывна
в точке![]() ,
то из Следствия3.1вытекает
следующее представление:
,
то из Следствия3.1вытекает
следующее представление:
|
|
|
|
|
|
|
|
|
|
Следствие 3.2
Если ![]() --
точка непрерывности функции
--
точка непрерывности функции![]() ,
то
,
то
![]()
Примеры абсолютно непрерывных распределений
1) Равномерное распределение в
отрезке ![]()
|
|
|
2) Показательное распределение с
параметром ![]()
![]()
|
|
|
Показательное распределение называют также экспоненциальным.
3) Нормальное (или гауссовское) распределение ![]() ,
,![]() ,
,![]() :
:

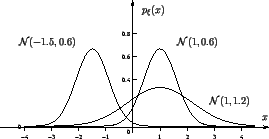
Стандартное нормальное
распределение -- ![]() :
:
|
|
|
Плотность распределения удовлетворяет свойствам:
![]() и
и  .
.
И наоборот, любая интегрируемая
функция ![]() ,
удовлетворяющая этим свойствам, может
быть взята в качестве плотности
распределения некоторой случайной
величины.
,
удовлетворяющая этим свойствам, может
быть взята в качестве плотности
распределения некоторой случайной
величины.
Поскольку функция распределения является функцией верхнего предела от плотности, то последняя восстанавливается по ней дифференцированием:
![]() .
.