Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Московский_государственный_технический_университет

.pdf

Скачиваний:

118

Добавлен:

23.03.2016

Размер:

1.25 Mб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

Московский государственный технический университет имени Н.Э. Баумана

Факультет «Фундаментальные науки» Кафедра «Математическая физика и вычислительная математика»

Б.Т. Добрица, И.В. Дубограй, О.В. Скуднева.

Криволинейные, поверхностные

интегралы и элементы теории поля.

методическое пособие к практическим занятиям.

Москва

Занятие 9. Криволинейный интеграл 1-го рода: определение, основные свойства, вычисление с помощью определенного интеграла. Формулировка теоремы существования криволинейного интеграла первого рода, независимость вычисления от направления обхода кривой. Физические приложения криволинейного интеграла первого рода: масса кривой, статистические моменты кривой относительно осей OX и OY ; моменты инерции кривой.

ОЛ-1 гл.5, ОЛ-2 гл.2, ОЛ-4 гл.3 § 9 Практика: ОЛ-6 №№ 2293, 2295, 2296, 2299, 2306, 2307 или ОЛ-5 №№

1.Определение криволинейного интеграла 1-ого рода.

Рассмотрим кусочно-гладкую кривую AB , в каждой точке М которой

задана функция	f M f x, y, z . Разобьѐм эту кривую на n малых частей
точками A0 ,..., Ai	,..., An	так, чтобы в точках каждой части	A A	значение
			i i 1

функции f Mi можно было считать постоянным, а сама часть могла быть принята за отрезок прямой (см. рис. 9.1). Пусть li - длина i-ой части разбиения. На каждой части выберем произвольную точку Mi xi , yi , zi и

Рисунок 9.1

составим интегральную сумму Sn f f M i li .

i 0

Определение. Криволинейным интегралом первого рода называется предел

интегральной суммы (если он существует) при неограниченном увеличении числа разбиений и стремлении длины каждой части к нулю.

f x, y, z dl		n
f x, y, z dl	lim	f Mi li .	(9.1)
AB	n	i 0
AB	max li 0	i 0

2.Свойства криволинейного интеграла 1 рода.

1.Независимость значения криволинейного интеграла первого рода от направления движения точки по кривой:

	f x, y, z dl			f x, y, z dl							(9.2)
AB		BA
2.Свойство линейность криволинейного интеграла:
	1 1	2	2		1	1	2		2	x, y, z dl
c f		x, y, z c f		x, y, z dl c		f	x, y, z dl c	f		x, y, z dl	(9.3)
AB						AB	AB
3. Свойство аддитивности:
	f x, y, z dl			f x, y, z dl			f x, y, z dl				(9.4)
ABC		AB				BC
4. Свойство монотонности.						Если f x, y, z g x, y, z на кривой АВ, то
	f x, y, z dl g x, y, z dl										(9.5)
AB		AB				f x, y, z непрерывна на кривой АВ, то
5. Теорема о среднем. Если						f x, y, z непрерывна на кривой АВ, то
существует число ζ такое, что							f x, y, z dl dl				(9.6)
							AB			AB

6. Криволинейный интеграл от единичной функции равен длине кривой:

LAB dl

(9.7)

3.Способы вычисления криволинейного интеграла 1 рода.

1.Если кривая задана в пространстве как пересечение двух поверхностей

F		x, y, z 0
	1	, то можно выразить из системы уравнений этих
AB :		, то можно выразить из системы уравнений этих
	F	x, y, z 0
	2

	y y x

поверхностей две переменные через третью, например,	z z x .

Тогда длина отрезка прямой dl dx2 dy2 dz2 1 y ' 2 z ' 2 dx и

	x
	f x, y, z dl B	f x, y x , z x	1 y ' x 2 z ' x 2 dx .	(9.8)
AB	xA

x x t

2.Если кривая задана параметрически уравнениями: y y t ,

то длина

z t

x ' t 2

y ' t 2

z ' t 2 dt , и

отрезка прямой dl

dx2 dy2

dz2

2 dt

(9.9)

, y

, z

x '

y '

z '

x, y, z dl

3.Если задана плоская кривая и в каждой еѐ точке определена функция

x, y , то формулы (9.8) и (9.9) упрощаются:

f x, y, dl B

f x, y x

1 y ' x 2 dx ,

(9.8а)

2 dt

(9.9а)

, y

x '

y '

x, y, dl

4.Если на плоскости кривая задана в полярной системе уравнением r r , то

2 d

cos , r

sin

r '

x, y dl

(9.10)

Примечание. а) Если контур интегрирования – отрезок прямой,

соединяющий точки A x1, y1, z1

и B x2 , y2 , z2 , то уравнения этого контура

имеют вид

x x1

y y1

z z1

t .

б) Если контуром интегрирования является эллипс

1, то удобно

перейти к параметрическому заданию этой кривой, где x a cost, y bsin t (частный случай – окружность с R a b ).

4.Теорема существования криволинейного интеграла 1 рода.

Если AB – кусочно-гладкая кривая и функция f M непрерывна на ней, то существует криволинейный интеграл I-го рода от этой функции (функция

		n
интегрируема по кривой AB ), то есть существует предел	lim	f Mi li
	n	i 0
	max li 0	i 0

и он не зависит от способа разбиения кривой на части и от выбора

промежуточных точек.

5.Физические приложения криволинейного интеграла первого рода. а) Масса материальной кривой.

Если x, y, z - линейная плотность кривой, то масса этой кривой

M x, y, z dl

(9.12)

б) Статистические моменты плоской кривой относительно осей OX и OY .

Moy	x x, y dl
	AB		(9.13)
Mox		y x, y dl

в) Координаты центра масс плоской кривой .

x	1		x x, y dl
x	M		x x, y dl
C	M
C
		AB	(9.14)
	1		(9.14)
y	1		y x, y dl
y	M		y x, y dl
C	M
C
		AB

г) Моменты инерции плоской кривой.

Joy	x2 x, y dl
	AB
Jox		y2 x, y dl	(9.15)
	AB		(9.15)
	AB

JO x2 y2 x, y dl

Формулы для решения задач в пространстве составляются аналогично.

6.Примеры решения задач.

Пример 9.1 (2299) Вычислим массу правого лепестка лемнискаты

r2 a2 cos 2 , если линейная плотность в каждой точке кривой x, y x y . Решение. Построим правую часть лемнискаты. Она лежит в секторе

. (См. рис.9.2)

4 4

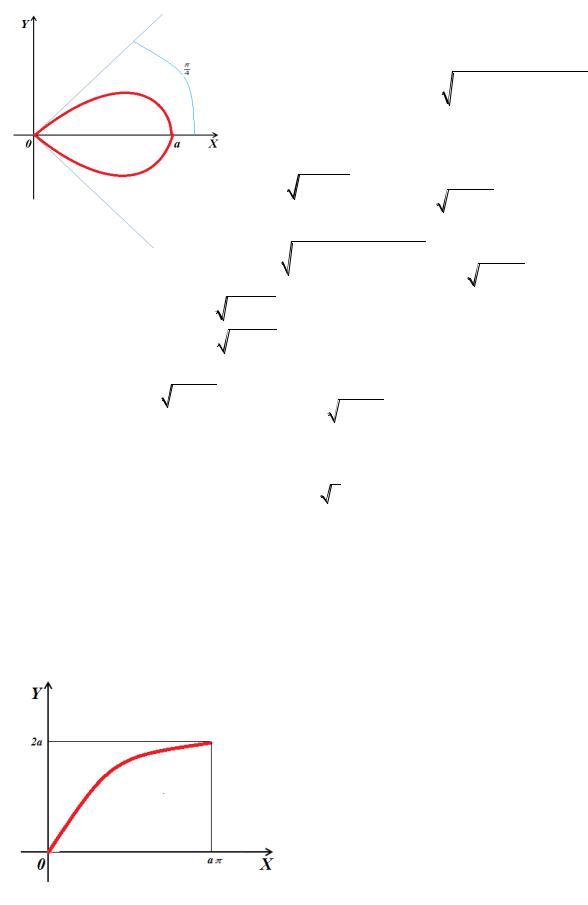
Рисунок 9.2

И учитывая, что

M x, y dl

Воспользуемся формулами (9.10) и (9.12).

M x, y dl

r cos , r

sin

r 2 r '

2 d

Упростим подкоренное выражение.

, r '

sin 2

r a

cos 2

r '

cos 2 .

cos 2 cos

x a

, подставим всѐ в рабочую формулу:

cos 2 sin

y a

cos sin

cos 2

После вычисления интеграла получим искомую массу


			4			.
						.
M		x, y dl a2		cos sin d a2	2
	AB
			4

Обратите внимание на то, что несмотря на симметричную форму лепестка лемнискаты, при составлении интеграла нельзя использовать эту симметрию,

		,
так как функция плотности не является чѐтной на интервале		,	.
	4		4

Пример 9.2. (2307) Найдѐм координаты центра тяжести полуарки циклоиды

t sin t

a 1 cost

Линейную плотность кривой будем считать равной единице.

Решение. Построим эскиз к задаче ( см.

рис. 9.3). Параметр t

вдоль кривой

меняется от

t 0

до t .

Воспользуемся формулами (9.9) ,

(9.12),

(9.14) при

1. Вычислим dl .

Т.к.

asin t

x '

a 1 cost

, y '

Рисунок 9.3

dl x ' t 2 y ' t 2 dt a 2 1 cost dt 2a sin 2t dt.

Подставим полученное выражение в формулы. Масса по формуле (9.12):

M 1 dl 2a sin

dt 4a.

По формулам (9.14) вычислим координаты искомой точки.

xdl

2a2

t sin t sin

cos t sin

ydl

Ответ: C

Пример 9.3. Вычислим момент инерции материальной кривой, которая является пересечением полусферы

Рисунок 9.4

(см. (9.15))

x2 y2

Кривая задана уравнениями

z y

x 4 y2 z2 и плоскости

z y , если плотность x2 y2 .

Решение. Построим обе заданные поверхности и линию их пересечения (см. рис. 9.4). Момент инерции

пространственной кривой
относительно начала координат
вычисляется по следующей
формуле:
JO x2 y2 z2 x, y, z dl .
	AB
z2 4	при x 0 .

Перейдѐм к еѐ параметрическому заданию. Заметим, что для точек кривой

x2 2 y2 4

выполняются уравнения .

z y

x 2cost
			при		t
	2 sin t						. (см. примечание б))
Тогда пусть y	2 sin t			2		2	. (см. примечание б))


z		2 sin t

При этом дифференциал дуги кривой

dl dx2 dy2 dz2 x ' t 2 y ' t 2 z ' t 2 dt 2dt ,

плотность 4cos2 t 2sin2 t .


2	4cos2 t 2sin2 t 2dt .
Подставляем всѐ в рабочую формулу: IO 4	4cos2 t 2sin2 t 2dt .

2
И после вычисления интеграла получаем ответ: IO 24 .

Занятие 10.

Определение криволинейного интеграла второго рода. Теорема существования и свойства. Вычисление криволинейного интеграла второго рода с помощью определенного интеграла для случаев явно заданной функции и параметрически заданной функции. Работа силы при перемещении материальной точки единичной массы из точки А в точку В вдоль кривой АВ. ОЛ-1 гл.5, ОЛ-2 гл.2, ОЛ-4 гл. 3 § 10 Практика: ОЛ-6 №№ Л 6 №№ 2310, 2313, 2314, 2315, 2325 или ОЛ-5 №№

10.72, 74, 76, 78.

Домашнее задание к занятию 10:ОЛ-6 №№ 2312, 2316, 2322, 2324 или ОЛ-5 №№ 10.71, 73, 77, 81.

1.Определение криволинейного интеграла второго рода.

Рисунок 10.1

Рассмотрим кусочно-гладкую кривую AB , в каждой точке М которой задана функция P x, y, z . Разобьѐм эту кривую на n малых частей точками

A0 ,..., Ai ,..., An	так, чтобы в точках каждой части	A A	значение функции
		i i 1

P Mi можно было считать постоянным, а сама часть могла быть принята за

отрезок прямой (см. рис. 10.1). Пусть xi xi 1 xi - проекция i-ой части разбиения на ось OX . На каждой части выберем произвольную точку

Mi xi , yi , zi и составим интегральную сумму Sn P P M i xi .

i 1

Определение. Криволинейным интегралом второго рода по переменной x называется предел последовательности интегральных сумм (если он существует) при неограниченном увеличении числа разбиений и стремлении длины каждой части к нулю. Такой интеграл обозначается следующим

образом:	P x, y, z dx .
	AB

По аналогии можно определить интегралы по переменным y и x :

Q x, y, z dy и	R x, y, z dz .	И тогда можно рассматривать
AB	AB
криволинейный интеграл второго рода общего вида
P x, y, z dx Q x, y, z dy R x, y, z dz			(10.1)

2.Теорема существования криволинейного интеграла 2-ого рода.

Если функция P x, y, z непрерывна в каждой точке кусочно - гладкой кривой, то она интегрируема по этой кривой по переменной x , т.е.

существует предел последовательности интегральных сумм

Sn P P M i xi и он не зависит от способа разбиения кривой на части и

i 1

выбора промежуточных точек.

	n
P x, y, z dx lim	P Mi xi .	(10.2)
n	i 1
max xi 0	i 1

3. Основные свойства криволинейного интеграла 2-ого рода.

1.Линейность. Криволинейный интеграл 2-ого рода от линейной комбинации интегрируемых по кривой функций равен линейной комбинации интегралов от этих функций. В частности,

	1	2	x, y, z dx		1			2
	P	x, y, z P	x, y, z dx		P	x, y, z dx		P	x, y, z dx .
AB				AB			AB

2.Аддитивность. Если кривая l AB разбита на две части, не имеющие

общих внутренних точек, то

Pdx Qdy Rdz Pdx Qdy Rdz Pdx Qdy Rdz .

3.Изменение знака при изменении направления движения по кривой.

Pdx Qdy Rdz Pdx Qdy Rdz .

Это свойство отличается от аналогичного свойства для ранее рассмотренных интегралов. Появление минуса связано с тем, что в соответствующей интегральной сумме при изменении направления перемещения точки по кривой изменит свой знак xi xi 1 xi . А следовательно, изменит знак и интеграл (см. (10.2)).

4.Вычисление криволинейного интеграла 2-ого рода.

Криволинейный интеграл 2-ого рода вычисляется так же, как

криволинейный интеграл 1-ого рода сведением к определѐнному. Для этого все переменные под знаком интеграла выражают через одну переменную,

используя уравнение той линии, вдоль которой производится

интегрирование.

а) Если линия АВ задана системой уравнений

y y x , z z x ,

то

P x, y, z dx Q x, y, z dy R x, y, z dz

(10.3)

x, y

, z

x, y

, z

x, y

, z

Для плоского случая,

когда кривая задана уравнением

y y x ,

криволинейный интеграл вычисляется по формуле:

P x, y dx Q x, y dy

(10.4)

P x, y x Q x, y x y

x dx .

Если линия АВ задана параметрическими уравнениями x x t , y y t , z z t , то

1 / 61 2 3 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.09.2019352.11 Кб5мой курсяк первая часть.docx
#
23.03.2016183.64 Кб25мой реферат.rtf
#
06.09.20191.22 Mб2мол.физ.откр.ф..docx
#
23.03.201628.85 Кб113Монголо татарское завоевание + последствия.docx
#
19.11.2019121.34 Кб6Морфологич. структура слова.doc
#
23.03.20161.25 Mб118Московский_государственный_технический_университет.pdf
#
24.12.201860.66 Кб1Мотивация труда посредством проектирования рабо....docx
#
23.03.2016154.82 Кб17Мощелкова_МУ к орг-эк части ДП.docx
#
27.10.20181.07 Mб10МОЯ ОБРАБОТАННАЯ.doc
#
17.09.201986.53 Кб6Моя шпора Тема 4.docx
#
09.02.20151.03 Mб13МОЯ Экономическая часть.doc