2004-matematicheskiy-analiz-differencial-noe-ischislenie-funkciy-odnoy-peremennoy-5mb

Пример 1.6.39

4

x4 + 5 x+ 2

Вычислить lim . x→0 x + 10

Решение

Пример 1.6.40

3

Вычислить lim (cos(2x))tg(5x) sinx .

x→π

Решение

Неопределенность вида 1∞. Для того чтобы раскрыть эту неопре- деленность представим основание в виде 1 + α(x), а в показателе вы- делим множитель 1/α(x):

Так как по второму замечательному пределу

1

lim (1+ x)x = e ,

x→0

то

1

lim (1+ cos(2x) − 1)cos(2 x)−1 = e.

x→π

Тогда

71

1.7. Непрерывность функций

Функция f(x) называется непрерывной в точке х0, если:

1)функция определена в некоторой окрестности точки х0, т.е. су- ществует такое число δ > 0, что Uδ (x0 ) D( f ) ;

2)существует конечный предел функции f(x) при х → х0;

3)предел функции f(x) при х → х0 равен значению функции в этой точке:

lim f (x) = f (x0 ).

x→ x0

Если функция непрерывна в каждой точке некоторой области, то она непрерывна в этой области.

Точки разрыва

Если в точке х0 нарушено хотя бы одно их этих условий, то х0 на- зывается точкой разрыва функции y = f(x). При этом различают три вида точек разрыва.

1. Точка х0 – точка устранимого разрыва, если существуют ко-

нечные пределы справа и слева при x → х0 и они равны между собой, но не равны значению функции в точке х0, либо функция не опреде- лена в данной точке:

В этом случае достаточно изменить значение функции только в одной точке x0 , чтобы получить новую функцию уже непрерывную

в точке x0 .

Приведем пример функции, имеющей точку устранимого разрыва.

Данную функцию можно доопределить до непрерывной, если задать

72

2. Точка х0 – точка разрыва первого рода, если существуют ко-

нечные пределы справа и слева при x → х0, но они не равны между собой:

Приведем пример функции, имеющей точку разрыва первого рода.

x − 1

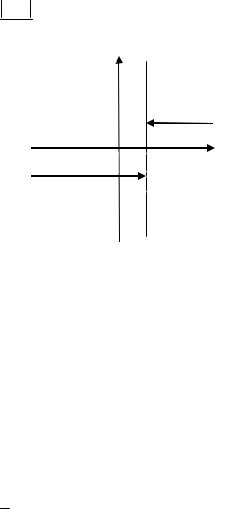
Пусть y = x − 1 , тогда х = 1 – точка разрыва (рис. 1.39).

Рис. 1.39

Получили, что существуют конечные пределы справа и слева при x → 1, но они не равны между собой. Следовательно, x = 1 – точка разрыва первого рода.

3. В остальных случаях имеем разрыв второго рода. Приведем пример функции, имеющей разрыв второго рода.

Пусть y = 1 , тогда х = 0 – точка разрыва (рис. 1.40). x

73

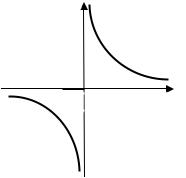
Y

Рис. 1.7.2

Следовательно, х = 0 – точка разрыва второго рода.

Свойства функций, непрерывных в точке

1. Если функции f(x) и g(x) непрерывны в точке х0, то функции

f(x) + g(x), f(x)g(x) и f(x) / g(x), при условии g(x0) ≠ 0, непрерывны в точке х0.

2.Если функция f(y) непрерывна в точке y0, а функция y = ϕ(x) не- прерывна в точке х0, причем y0 = ϕ(x0), то в некоторой окрестности точки х0 определена сложная функция f(ϕ(x)) и эта функция непре- рывна в точке х0.

3.Если функция f(x) непрерывна в точке х0, то она ограничена в некоторой окрестности этой точки.

Свойства функций, непрерывных на отрезке

1.Если функция f(x) непрерывна на отрезке [a, b] и на его концах принимает значения противоположные по знаку, т.е. f(a) f(b) < 0, то на интервале (a, b) существует по крайней мере одна точка, в ко- торой функция f(x) обращается в ноль.

2.Если функция f(x) непрерывна на отрезке [a, b] и f(a) = A ≠ f(b) = B, то для любого числа C (A, B) на интервале (a, b) найдется по край- ней мере одна точка с, в которой f(c) = C.

3.Если функция f(x) непрерывна на отрезке [a, b], то она ограни- чена на нем.

4.Если функция f(x) непрерывна на отрезке [a, b], то она на этом отрезке принимает свои наименьшее и наибольшее значения.

74

Пример 1.7.1

Найти точки разрыва функции f (x) = sin(x + 1) , определить ха- x + 1

рактер разрыва.

Решение

В точке х = –1 функция не определена, следовательно, х = –1 – точка разрыва функции. Раскроем модуль:

Найдем пределы функции при x → −1 − 0 и при x → −1 + 0:

Получили, что существуют конечные пределы справа и слева при x → −1, но они не равны между собой. Следовательно, x = −1 – точ- ка разрыва первого рода.

Пример 1.7.2

Вточках x = 2 и x = 1 функция не определена, следовательно, x = 2

иx = 1 – точки разрыва функции.

Найдем пределы функции при x → 2 − 0 и при x → 2 + 0:

Следовательно, х = 2 – точка разрыва второго рода.

75

Найдем пределы функции при x → 1 − 0 и при x → 1 + 0:

Следовательно, x = 1 – точка разрыва второго рода.

Таким образом, получили x = 1 и х = 2 – точки разрыва второго рода.

Пример 1.7.3

характер разрыва.

Решение

Вточках x = −2 и x = −1 функция не определена, следовательно,

x= −2 и x = −1 – точки разрыва функции.

Найдем пределы функции при x → −2 − 0 и при x → −2 + 0:

Получили, что существуют конечные пределы справа и слева при x → −2 и они равны между собой. Следовательно, x = −2 − точка устранимого разрыва. В этой точке мы можем доопределить функ- цию до непрерывной:

−1, если x = −2.

76

Найдем пределы функции при x → −1 − 0 и при x → −1 + 0:

Следовательно, x = −1 – точка разрыва второго рода.

Итак, x = −2 − точка устранимого разрыва, x = −1 – точка разрыва второго рода.

1.8. Асимптоты графиков функций

Пусть f(x) – некоторая функция, тогда для нахождения асимптот этой функции используются следующие формулы:

1) прямая, заданная уравнением х = а, является вертикальной асимптотой, если

lim f (x) = ∞;

x→a

2) прямая, заданная уравнением y = kx+b, является наклонной асимптотой, если

k = lim f (x) ;

x→∞ x

b = lim ( f (x) − kx).

x→∞

При этом указанные пределы могут быть различными при х → ∞

(для правой наклонной асимптоты) и при х → – ∞ (для левой на- клонной асимптоты);

3) при k = 0 получаем горизонтальную асимптоту.

Пример 1.8.1

Построить эскиз графика функции y = 2x2 + 1 . x + 4

Решение

1.Область определения: x (−∞, −4) (−4, ∞).

2.Функция не является ни четной, ни нечетной, так как

77

3.Найдем точки пересечения графика функции с осью OY. Пусть

x= 0, тогда y = 1/4, следовательно, точка (0, 1/4) – точка пересечения графика с осью OY.

4.Найдем точки пересечения графика функции с осью OX. Пусть

y= 0, тогда

2x2 + 1 = 0; x + 4

2x2 + 1 = 0.

Данное уравнение решений не имеет, а значит, график функции не пересекает ось OX.

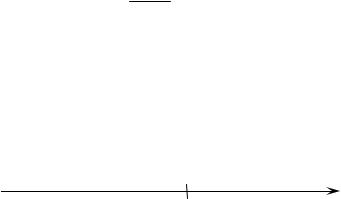
5. Найдем промежутки постоянства знака значений функции. От- метим на числовой прямой точки, в которых числитель и знамена- тель равны нулю, и определим знаки получившихся интервалов:

6. Найдем асимптоты графика функции. Так как

то x = −4 – уравнение вертикальной асимптоты. Наклонную асимптоту найдем по формуле y = kx + b, где

x

78

x

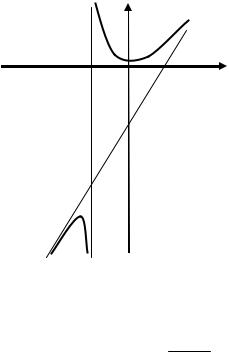
Получили y = 2x − 8 – уравнение наклонной асимптоты.

Найдем точки пересечения наклонной асимптоты с осями координат:

7. Построим эскиз графика функции (рис. 1.41).

Рис. 1.41

Пример 1.8.2

Построить эскиз графика функции y = 16 − x2 .

4x − 6

Решение

1.Область определения: x (−∞, 3/2) (3/2, ∞).

2.Функция не является ни четной, ни нечетной, так как

79

3. Найдем точки пересечения графика функции с осью OY.

Пусть x = 0, тогда y = −8/3, значит, точка (0, −8/3) – точка пересе- чения графика с осью OY.

4. Найдем точки пересечения графика функции с осью OX. Пусть y = 0, тогда

16 − x2 = 0 16 − x2 = 0 x = ±4. 4x − 6

Следовательно, точки (4, 0) и (−4, 0) – точки пересечения с графи- ка осью OX.

5. Найдем промежутки постоянства знака значений функции. Отметим на числовой прямой точки, в которых числитель и зна-

менатель равны нулю, и определим знаки получившихся интервалов

6. Найдем асимптоты графика функции. Так как

то x = 3/2 – уравнение вертикальной асимптоты. Наклонную асимптоту найдем по формуле y = kx + b, где

x

80