
2004-matematicheskiy-analiz-differencial-noe-ischislenie-funkciy-odnoy-peremennoy-5mb
.pdf
|
+ |
4 |
|
lim 1 |
|
|
|
n→∞ |
|
2n2 + 5n + 3 |
|
2n2 +5n+3
4 |
= e. |
|
Тогда
|
|
|
|
|
|
|
|
|
4 |
|
2n2 +5n+3 |
|
|
4n |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4 |
|
|
n |
2n2 +5n+3 |
4 |
|
lim |
|
|
||||||
|
|
|
|
2 |
|
|
|
||||||||||
lim 1+ |
|
|
|
|
|
|
|
|
|
|
= en→∞ 2n |
+5n+3 |
= |
||||
n→∞ |
2n2 + 5n + 3 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
lim |
|
|
4/ n |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
= e0 = 1. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
= en→∞ 2+5/ n+3/ n2 |
|
|
|
|
||||||||||
Пример 1.5.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n3 |
− 2 |
|
2n−n3 |
|
|
|
|
|
|
|
||||||
Вычислить |
|
|
|
|
|
|
|
|
|
|
|
||||||
lim |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||
|
n3 |
+ 1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение
Неопределенность вида 1∞. Для того чтобы раскрыть эту неопре- деленность, представим основание в виде 1 + α(x), а в показателе вы- делим множитель 1/α(x):
n3 |
− 2 |
2n−n3 |
∞ |
|
|
|
n3 + 1− |
3 |
|
2n−n3 |
|
|
|
|
|
|
|
−3 2n−n3 |
||||||||||||||
lim |
|
|
|
= (1 |
) |
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
= lim 1 |
+ |
|
|
|
|
|
= |
||||||
|
+ 1 |
|
|
n3 + 1 |
|
|
|
|
|
n3 |
|
|
||||||||||||||||||||
n→∞ n3 |
|
|
|
n→∞ |
|
|
|
|
|
|
|
n→∞ |
|
+ 1 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
n3 +1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
( |
2n−n |
|
) |
− |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
+1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
= lim |
1− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
n3 |
+ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Так как по второму замечательному пределу lim |
|
+ |
1 n |
= e , то |
||||||||||||||||||||||||||||
1 |
|
|
||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
n |
|
||||
Тогда
lim 1−
n→∞
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
n3 +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
lim |
1− |
|
|
|
|
|
|
|
|
|
|
|
|
= e. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
n3 |
+ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
n→∞ |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
3 |
|
|
|
|
3 |
|
n3 +1 |
|
|
|
3 |
|
|
||||||
|
|
( |
2n−n |
|
) |
− |
|
|
|
|
|
|
− |
|
|
|
|
|
−3(2n−n |
|
) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3 |
|
|
|
|
n |
3 |
|
|
|
|
|
3 |
|
|
|
lim |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
+1 |
|
|
|
= e |
|
|
= |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
n +1 |
|
|||
n3 + 1
lim |
3n3 |
−6n |
lim |
3−6 / n2 |
|
= en→∞ n3 |
+1 |
= en→∞ 1+1/ n3 |
= e3. |
||
41

Пример 1.5.9 |
( n + 5 − n − 4 ). |
Вычислить lim |
|
n→∞ |
|
Решение
Неопределенность вида ∞ – ∞. Домножим и разделим выражение, стоящее под знаком предела, на сопряженное к нему выражение
n + 5 + n − 4 , после чего воспользуемся формулой разности квадратов (a − b)(a + b) = a2 – b2:
lim ( |
n + 5 − n − 4 ) = lim |
|
( n + 5 − |
n − 4 )( |
n + 5 + |
|
n − 4 ) = |
|||||||
n→∞ |
|
n→∞ |
( |
n + 5 + |
n − 4 ) |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
= lim |
n + 5 − n + 4 |
= lim |
|
9 |
|
|
= |
9 |
|
|
= 0. |
||
|
|
|
|
|
|
|
|
|||||||
|
n→∞ n + 5 + n − 4 |
|
n→∞ n + 5 + |
n − 4 ∞ |
|
|
||||||||
Пример 1.5.10
Вычислить nlim→∞ (3 8 − n3 + n).
Решение
Неопределенность вида − ∞ + ∞. Домножим и разделим выражение, стоящее под знаком предела, на сопряженное к нему выражение
(3 8 − n3 )2 − n3 8 − n3 + n2 , после чего воспользуемся формулой суммы кубов (a + b)(a2 – a b + b2) = a3 + b3:
|
|
|
|
|
(3 8 − n3 ) |
2 |
− n3 8 |
− n3 |
+ n2 |
|
|
|
||||||
|
|
(3 8 − n3 + n) |
|
|
|
|
||||||||||||
lim (3 8 − n3 + n)= lim |
|
|
2 |
|
|
|
|
|
|
|
|
|
= |
|||||
n→∞ |
n→∞ |
(3 8 − n3 ) − n3 8 − n3 + n2 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
= lim |
8 − n3 |
+ n3 |
= lim |
|
|
8 |
|
|
= |
|
8 |
= 0. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
n→∞ (3 8 − n3 )2 − n3 8 − n3 + n2 |
n→∞ (3 8 − n3 )2 − n3 8 − n3 + n2 |
|
|
∞ |
|
|
||||||||||||
Пример 1.5.11 |
|
|
|
|
|
|
2n2 + nsin2 |
|
|
|
|
|
|
|
|
|||
Вычислить предел последовательности |
lim |
|
n |
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
n→∞ n2 + 5n |
+ cos n |
|
|
|
|
|
||||||
42

Решение
Разделим числитель и знаменатель на n в наибольшей степени, т.е. на n2:
|
2n2 + nsin2 n |
|
|
|
2 |
+ |
|
sin2 n |
|
|
||
lim |
= lim |
|
|
|
|
n |
. |
|||||
|
|
|
|
|
5 |
|
|
cos n |
||||
n→∞ n2 + 5n + cos n |
n→∞ |
1 |
+ |
|
+ |
|
||||||
|
|
|
|
n |
n2 |
|
||||||
|
|
|
|
|
|
|
|
|
||||
Последовательность {sin2n} – ограниченная последовательнось, а последовательность {1/n} – бесконечно малая. Произведение беско- нечно малой последовательности на ограниченную последователь- ность является бесконечно малой. Следовательно,
|
sin2 n |
|
1 |
|
|
lim |
|
= lim sin2 n |
|
|
= 0. |
|
|
||||
n→∞ n |
n→∞ |
n |
|
||
Аналогично, последовательность {cos n} – ограниченная, а после- довательность {1/n2} – бесконечно малая. Следовательно,
|
|
|
|
|
|
|
lim |
cos n |
|
= 0. |
|
|
||||
|
|
|
|
|
|
n2 |
|
|
||||||||
|
|
|
|
|
|
n→∞ |
|
|
|
|
||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + sin2 n |
|
2 + 0 |
|
|
||||||||
|
lim |
|
|
|
|
|
n |
|
|
= |
|
= 2. |
||||
|
|
|
5 |
|
|
|
|
1+ 0 + |
0 |
|||||||
n→∞ |
1+ |
+ |
cos n |
|
|
|||||||||||
|
|
|
n |
n2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 1.5.12 |
( |
|
|
|
|
|
|
n )cos(πn). |
|
|
||||||
Вычислить lim |
n + 1 − |
|
|
|||||||||||||
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
( |
|
|
|
|
|
|
n ). |
|
|
|
|
|||
Вычислим lim |
|
n + 1 − |
|
Неопределенность вида ∞ – ∞. |
||||||||||||
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Домножим и разделим выражение, стоящее под знаком предела, на
сопряженное к нему выражение n +1 + n , после чего воспользуемся формулой разности квадратов (a − b)(a + b) = a2 – b2:
lim |
( n + 1 − |
n ) = lim ( |
n + 1 − |
n )( |
n + 1 + |
n ) = lim |
n + 1− n |
|
= |
||||
n + 1 + n |
|
|
|
||||||||||
n→∞ |
|
n→∞ |
|
n→∞ n + 1 + |
n |
||||||||
|
|
= lim |
1 |
|
= |
|
1 |
|
= 0. |
|
|
|
|
|
|
n + 1 + |
|
|
|
|
|
||||||
|
|
n→∞ |
n |
∞ |
|
|
|
|
|
||||
43

Последовательность {cos(πn)} – ограниченная последовательнось, а последовательность { n + 1 − n} – бесконечно малая. Произведе-
ние бесконечно малой последовательности на ограниченную после- довательность является бесконечно малой. Следовательно,
lim |
( n + 1 − n )cos(πn) = 0. |
n→∞ |
|
1.6. Предел функции
Любой интервал, содержащий точку x0, называется окрестностью
точки x0. Интервал Uδ(x0) = (x0 – δ, x0 + |
δ) называется δ-окрест- |
||||
|
|
|
|
|
|
ностью точки. x0. Интервал U δ (x0 ) = {x : 0 |
< |
|
x − x0 |
|
< δ} называется |
|
|
||||
проколотой δ-окрестностью точки x0.
Функция f(x), называется ограниченной в окрестности U(x0) точки x0, если существует такое число М > 0, что │f(x)│ < M для любого
x U(x0).
Определение предела функции
1. По Коши.
Пусть функция y = f(x) определена в некоторой проколотой окрест-
ности U (x0 ) = (x0 − r, x0 ) (x0 , x0 + r) точки x0, где r > 0 – некоторое число. Тогда число a называется пределом функции f(x) в точке х0 и обо-
значается lim f (x) = a , если для любого положительного числа ε (ε > 0)
x→ x0
существует такое положительное число δ(ε), зависящее от ε, что для
всех x U (x0 ) и удовлетворяющих неравенству 0 < │x – x0│ < δ(ε), бу-
дет верно неравенство │f(x) – a│ < ε. Или с помощью логических сим- волов:
lim f (x) = a ε > 0 δ(ε) > 0 : x : 0 < x − x0 < δ f (x) − a < ε.
x→ x0
Также определение предела функции можно записать, используя понятие окрестности:
lim f (x) = a ε > 0 δ(ε) > 0 : x U δ (x0 ) f (x) − a < ε.
x→ x0
44
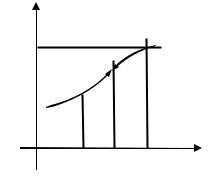
Данное определение можно проиллюстрировать следующим обра- зом (рис. 1.38). Возьмем число ε > 0 и на оси OY отметим ε-окрестность точки а, т.е. интервал (а − ε, а + ε), через концы которо- го проведем прямые, параллельные оси OX. Получим полосу шириной 2ε. Если для любого ε > 0 можно указать такое положительное чис- ло δ, что график функции y = f(x), рассмотренный для всех x из δ-окрестности точки x0 и не равных x0, целиком находится в этой поло- се, то число а является пределом функции f(x) при x, стремящемся к x0.
Y
а+ ε
а
а− ε 

O |
x0 − δ x0 |
x0 + δ |
X |
Рис. 1.38
2. По Гейне.
Пусть функция y = f(x) определена в некоторой проколотой окре-
стности U (x0 ) точки x0. Тогда число a называется пределом функции f(x) в точке х0, если для любой последовательности {xn} значений
аргумента x U (x0 ) , сходящейся к точке х0, соответствующая по- следовательность значений функции {f(xn)} сходится к числу а.
Односторонние пределы
Пусть функция y = f(x) определена в некоторой правой проколо-
той окрестности U + (x0 ) = (x0 , x0 + r) точки x0, где r > 0 – некоторое число. Число а называется пределом функции при х → x0 + 0 справа
( lim f (x) = a) , если для любого ε > 0 существует такое положи- |
|
x→ x0 +0 |
|
|
+ (x ) из |
тельное число δ(ε) > 0, зависящее от ε, что для любого x U |
|
|
0 |
условия 0 < x – x0 < δ(ε) следует условие│f(x) – a│ < ε.
45
Пусть функция y = f(x) определена в некоторой левой проколотой
окрестности U − (x0 ) = (x0 − r, x0 ) точки x0, где r > 0 – некоторое чис-
ло. Число а называется пределом функции при х → x0 – 0 слева
( lim f (x) = a ), если для любого ε > 0 существует такое положи- |
|
x→ x0 |
−0 |
|
|
тельное число δ(ε) > 0, зависящее от ε, что для x U |
|
− (x ) из усло- |
||||||||
|
|
|
0 |
|
|
|
|
|||
вия –δ(ε) < x – x0 < 0 следует условие │f(x) – a│ < ε. |
|
|
|
|
|
|
|
|
||
Или с помощью логических символов: |
|
|
|
|
|
|
|
|
||
lim |
f (x) = a ε > 0 |
δ(ε) > 0 : x : 0 < x − x0 < δ |
|
f (x) − a |
|
< ε; |
||||
|
|
|||||||||
x→ x0 +0 |
f (x) = a ε > 0 |
δ(ε) > 0 : x : −δ < x − x0 < 0 |
|
f (x) − a |
|
< ε. |
||||
lim |
|
|
||||||||
|
|
|||||||||
x→ x0 −0 |
|
|
|
|
|
|
|
|
|
|
Предел в бесконечности
Пусть функция y = f(x) определена для всех x, таких, что │x│ > r, где r > 0 – некоторое положительное число. Число а называется преде-
лом функции при х → ∞ ( lim f (x) = a ), если для любого ε > 0 сущест-
x→∞
вует такое положительное число δ(ε) > 0, зависящее от ε, что для лю- бого х из условия │x│ > δ(ε) следует неравенство │f(x) – a│ < ε.
Пусть функция y = f(x) определена для всех x, таких, что x > r.
Число а называется пределом функции при х → +∞ ( lim f (x) = a ),
x→+∞
если для любого ε > 0 существует такое положительное число δ(ε) > 0, зависящее от ε, что для любого х из условия x > δ(ε) следует неравен- ство │f(x) – a│ < ε.
Пусть функция y = f(x) определена для всех x, таких, что x < −r.
Число а называется пределом функции при х → −∞ ( lim f (x) = a ),
x→−∞
если для любого ε > 0 существует такое положительное число δ(ε) > 0, зависящее от ε, что для любого х из условия x < −δ(ε) следует неравен- ство │f(x) – a│ < ε.
Основные теоремы о пределе функции
1.Пусть при x → x0 существуют конечные пределы функций f1(x)
иf2(x). Тогда при x → x0 также существуют пределы суммы, разности
ипроизведения этих функций, при этом
lim ( f1 (x) ± f2 |
(x)) = lim f1 |
(x) ± lim f2 (x); |
x→ x0 |
x→ x0 |
x→ x0 |
46
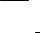
lim ( f1 (x) f2 |
(x)) = lim f1 |
(x) lim f2 (x). |
x→ x0 |
x→ x0 |
x→ x0 |
Кроме того, если lim |
f2 (x) ≠ 0 , то существует предел частного |
|||||||
x→ x0 |
|
|
|
|
|
|
|
|
этих функций: |
|
|
|
|
|
|
|
|
|
f1 |
(x) |
|
|
lim |
f1 |
(x) |
|
lim |
|
= |
x→ x0 |
|
|
. |
||
|
|
|
|
|
||||
x→ x0 |
f2 |
(x) |
|
lim |
f2 |
(x) |
||
|
|
|
|
|
x→ x0 |
|
|
|
2. Если при x → x0 функция f(x) имеет предел, то этот предел единственный.
3. Если g(x) ≤ f(x) для всех x U (x0 ) и функции g(x) и f(x) имеют в точке x0 предел, то
lim g(x) ≤ lim f (x).
x→ x0 x→ x0
4. Если ϕ(x) ≤ f(x) ≤ g(x) для всех x U (x0 ) и функции ϕ(x) и g(x) в точке x0 имеют один и тот же предел, равный а, то и функция f(x) в точке x0 имеет предел, равный этому же числу:
lim |
f (x) = lim ϕ(x) = lim g(x) = а. |
|
x→ x0 |
x→ x0 |
x→ x 0 |
5.Если функция f(x), определенная в окрестности точки x0, имеет
вэтой точке конечный предел, то она ограничена в некоторой окре- стности этой точки.
6. Если существует lim |
f (x), то для любого числа С |
x→ x0 |
|
lim (Cf (x)) = C lim f (x). |
|
x→ x0 |
x→ x0 |
7. Если функция f(x) = С – постоянная в некоторой проколотой
окрестности точки x0, то lim f (x) = C.
x→ x0
Замечательные пределы
Частое применение находят следующие пределы:
lim sin x = 1 – первый замечательный предел,
x→0 x
1
lim(1+ x) x = e – второй замечательный предел
x→0
47

или
|
|
1 |
x |
|
lim 1 |
+ |
|
|
= e. |
|
||||
x→∞ |
|
x |
|
|
|
|
|
|
Арифметика бесконечностей |
||
Пусть С = const, С ≠ 0, тогда: |
|
|||||
1) С ∞ = ∞; |
8) (+∞)С = +∞, С > 0; |
|||||
2) |
|
C |
|
= ∞; |
9) (+∞)С = 0, С < 0; |
|
0 |
||||||
|
|
|
|
|
||
|
|
C |
|
|||
3) |
|
|
= 0 ; |
10) (С)+∞ = +∞, С > 1; |
||
|
∞ |
|||||
4) |
∞ + С = ∞; |
11) |
(С)−∞ = 0, С > 1; |
5) |
+∞ + ∞ = +∞; |
12) |
(С)+∞ = 0, 0 < С < 1; |
6) |
–∞ – ∞ = –∞; |
13) |
(С)−∞ = +∞, 0 < С < 1; |
7) |
(+∞)+∞ = +∞; |
14) |
n +∞ = +∞ . |
|
|
|
|
Неопределенности |
|
|
Если |
при |
вычислении пределов получаются выражения вида |
||
0 |
; 0 ∞; |
∞ |
; |
∞ − ∞; 1∞ ; 00 ; ∞0 , называемые неопределенностями, то |
|
0 |
∞ |
||||
|
|
|
|||
необходимо с помощью преобразований избавиться от этих неопре- деленностей.
Эквивалентные функции
Пусть функции f(x) и g(x) определены в некоторой проколотой ок- рестности точки x0 и отличны от нуля во всех точках этой окрестно- сти. Функции f(x) и g(x) называются эквивалентными при x → x0, если предел их отношения при x → x0 равен единице:
f (x) g(x) при x → x |
lim |
f (x) |
= 1. |
|
|||
0 |
x→ x0 |
g(x) |
|
|
|||
Пусть функция f(x) эквивалентна функции f1(x), а функция g(x) эк- вивалентна функции g1(x) при x → x0. Тогда, если существует
lim |
f1 (x) |
, то существует и lim |
f (x) |
, причем |
||||
|
|
|||||||
x→ x0 |
g (x) |
x→ x0 g(x) |
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
lim |
f (x) |
= lim |
f1 (x) |
. |
||
|
|
|
|
|||||
|
|
x→ x0 |
g(x) |
x→ x0 |
g (x) |
|||
|
|
|
|
|
|
|
1 |
|
48

Бесконечно большие функции
Пусть функция f(x) определена в некоторой проколотой окрестно-
сти U (x0 ) точки x0. Тогда функция f(x) имеет в этой точке бесконеч-
ный предел ( lim f (x) = ∞ ), если для любого сколь угодно большого
x→ x0
числа Е > 0 существует такое число δ(Е) > 0, зависящее от Е, что для
любого x U (x0 ) из условия 0 < │x – x0│ < δ(Е) следует условие │f(x)│ > E. Или с помощью логических символов:
lim f (x) = ∞ Е > 0 δ(E) > 0 : x : 0 < x − x0 < δ f (x) > E.
x→ x0
Если lim f (x) = ∞ , то функцию f(x) называют бесконечно большой.
x→x0
Бесконечно малые функции
Пусть функция α(x) определена в некоторой проколотой окрест-
ности U (x0 ) точки x0. Функция α(x) называется бесконечно малой при x → x0, если
lim α(x) = 0.
x→ x0
Одна и та же функция может быть бесконечно малой или не быть в зависимости от того, к какому значению стремится x. Например, функция α(x) = cos x – бесконечно малая функция при x → π/2, так
как lim cos x = 0 , но функция cos x не является бесконечно малой
x→π / 2
функцией при x → 0, так как lim cos x = 1.
x→0
Сравнение бесконечно малых функций
Пусть функции α(x) и β(x) определены в некоторой проколотой ок- рестности точки x0 и отличны от нуля во всех точках этой окрестности. Бесконечно малые при x → x0 функции α(x) и β(x) называются эквива- лентными если предел их отношения при x → x0 равен единице:
α(x) β(x) lim |
α(x) |
= 1. |
|
||
x→ x0 |
β(x) |
|
Бесконечно малые при x → x0 функции α(x) и β(x) называются сравни-
мыми, если существует хотя бы один из пределов lim |
α(x) |
или lim |
β(x) |
. |
|
|
|||
x→x0 β(x) |
x→x0 α(x) |
|||
49

Бесконечно малые при x → x0 функции α(x) и β(x) называются беско-
нечно малыми одного порядка малости, если
lim α(x) = C ≠ 0.
x→ x0 β(x)
Бесконечно малая при x → x0 функция α(x) называется бесконечно ма-
лой более высокого порядка малости, чем бесконечно малая β(x),если
lim α(x) = 0.
x→ x0 β(x)
Обозначение: α(x) = o(β(x)).
Бесконечно малая при x → x0 функция α(x) имеет порядок малости r (r > 0) относительно бесконечно малой β(x), если
lim |
α(x) |
= C ≠ 0. |
|
||
x→ x0 (β(x))r |
|
|
Свойства бесконечно малых функций
1.Сумма (разность) двух бесконечно малых при x → x0 функций есть бесконечно малая функция при x → x0.
2.Произведение бесконечно малой функции при x → x0 на огра- ниченную в некоторой проколотой окрестности точки x0 функцию есть бесконечно малая функция при x → x0.
3.Сумма двух бесконечно малых при x → x0 функций разного по- рядка малости есть бесконечно малая функция меньшего порядка.
Из определения предела функции следует, что число а является пределом функции f(x) в точке x0 тогда и только тогда, когда эта
функция представима в виде f(x) = a +α(x), где α(x) − бесконечно ма- лая функция при x → x0.
Таблица эквивалентных бесконечно малых функций
Пусть α(x) → 0, тогда
sin α(x) ~ α(x); tg α(x) ~ α(x);
1 – cos α (x) ~ 1 α2 (x); 2
50
