2004-matematicheskiy-analiz-differencial-noe-ischislenie-funkciy-odnoy-peremennoy-5mb

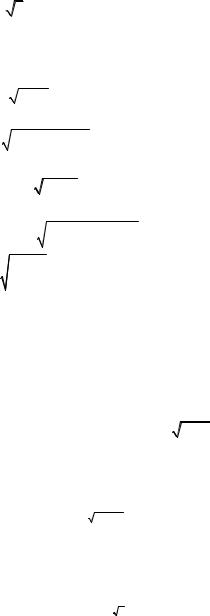
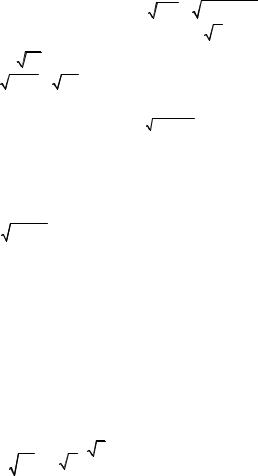
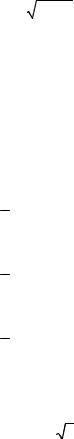3)y = a 3 x(x + d )2 ;

4)y = ec( x+d ) ;

+d )b(x

Задача 14. Разложить многочлен dx4 + kx3 + mx2 + bx + a по фор- муле Тейлора в точке х0 = 2.

191

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Разделить многочлен f(x) на многочлен g(x), если

f(x) = x3 + 3x2 + 3x + 1, g(x) = x + 1.

2. Найти область допустимых значений функций:

а) y = 2 − x ; 5 + x

б) y = log5(x – 1).

3. Выяснить, являются ли четными или нечетными функции:

4. Нарисовать графики функций:

а) y = 1 ; x3

б) y = 5 x;

в) y = log1/2x; г) у = 2x.

5. Построить графики функций:

а) y = 2 + x ; 3 − x

б) y = 2 + x ; 3 − x

в) y = 2 + x ; 3 − x

г) y = arccos(1− 3x) + 2;

д) y = 2x − 3 + 4;

е) y = e 4− x ;

ж) y = sin(3x + 5) .

6.Дать определение предела последовательности.

7.Дать определение ограниченной последовательности.

192

8. Вычислить предел последовательности:

9.Привести пример последовательности, не имеющей предела.

10.Дать определение предела функции.

11.Найти пределы функций:

12.Перечислить основные свойства пределов функций (предел суммы, произведения и частного).

13.Записать первый и второй замечательные пределы функций.

14.Дать определение бесконечно малой функции.

15.Найти пределы функций:

16.Дать определение предела при х → ∞.

17.Дать определение пределов функций при x → x0 – 0 и при x → x0 + 0.

18.Вычислить предел функции:

193

19.Дать определение эквивалентных бесконечно малых.

20.Найти эквивалентные бесконечно малые при α(х) → 0 для функций:

а) sin α(x); б) 1–cos α(x);

в) loga(1+α(x)); г) аα(x)–1.

языке ε-δ.

22. Вычислить пределы функций:

23.Дать определение бесконечно большой функции.

24.Дать определение ограниченной функции.

25. Определить порядок малости бесконечно малой функции α(x) = 9 + 2xtg(4x) − 3 относительно бесконечно малой β(x) = 5x2 +1 − 5 при х → 0.

26.Дать определение непрерывности функции в точке.

27.Какие существуют виды точек разрыва? Привести примеры.

28.Сформулировать свойства функций непрерывных в точке.

29.Сформулировать свойства функций непрерывных на отрезке.

30.Найти точки разрыва и исследовать характер функций:

194

31. Найти все асимптоты графика функции и построить эскиз гра- фика функции:

32.Дать определение производной функции в точке.

33.Продолжить формулы:

34. Найти производные функций:

а) y = x3 − x;

б) y = 2x + sin x; в) y = log3 x + 4.

195

35. Продолжить формулы:

(arcsin x)'= …; (arcctg x)'= …;

(arсcos x)'= …

36.Написать правило нахождения производной сложной функции.

37.Найти производные функций:

а) y = sin (2x);

б) y = 251− x2 ;

в) y = tg2x.

38.Дать определение логарифмической производной.

39.Найти производные функций:

а) y = log2 (1− x);

б) y = arcsin2(4x2 – 1);

в) y = 3 arcctg 1 ; x

г) y = cosxarcsin x.

40.В чем заключается геометрический смысл производной функ- ции в точке?

41.Написать уравнение касательной и нормали к графику функций:

а) y = x в точке c абсциссой х0 = 4; б) x = ln x в точке c абсциссой х0 = е;

в) y = arcsin x − 1 в точке c абсциссой х0 = 1.

2

42.Дать определение дифференциала первого порядка.

43.Написать формулу Тейлора с остаточным членом в форме Пеано.

196

50. Написать уравнение касательной и уравнение нормали к гра- фику функции y = e−4x2 + arcsin x в точке c абсциссой х0 = 0.

51. Написать уравнение касательной и уравнение нормали к гра- фику функции y = (3 + sin(πx))2 x в точке c абсциссой х0 = 1.

197

52. Выяснить, будет ли функция

непрерывной и дифференцируемой в точке х0 = 0 (ответ обосновать). 53. Используя формулу Лейбница, найти десятую производную

функций:

а) f (x) = sh(2x)(2x2 + 3x − 1); б) f (x) = 2− x (x2 + 2x).

54. Выяснить, будет ли функция y = 3 (x2 − 4x + 3)2 дифференци- руемой в точке х0 = 1 (ответ обосновать).

55.Дать определение монотонной функции. Сформулировать дос- таточное условие монотонности функции.

56.Найти точки экстремума и интервалы монотонности функции

y= 2x − 33 (x − 2)2 − 2 .

57.Дать определение убывающей функции.

58.Сформулировать необходимое условие локального экстремума функции в точке.

59.Сформулировать достаточные условия локального экстремума функции в точке.

60.Найти интервалы возрастания, убывания и точки экстремума функций:

а) y = 2x2 − 1; x

б) y = 1 x5 − 1 x3; 5 3

в) y = 3 x2 − 1.

61.Сформулировать достаточные условия существования точки перегиба.

62.Найти наибольшее и наименьшее значения функции

f (x) = 3 2(x − 2)2 (5 − x) на отрезке [1; 5].

63.Найти промежутки возрастания и убывания, точки экстремума

инарисовать график функции f (x) = (x − 2)3 3 x2 .

64.Сформулировать теорему Коши.

198

65.Проверить справедливость теоремы Коши для функций y = x3

иy = x2 + 1 на отрезке [1; 2].

66.Сформулировать теорему Ролля.

67.Проверить справедливость теоремы Ролля для функции y = x + 3 на отрезке [−4, −2].

68.Сформулировать теорему Лагранжа.

69.Написать формулу Лагранжа для функций y = ln x на отрезке

[1, e].

70.Написать формулу Тейлора 3-го порядка для функции y = (x2 –

–3x + 1)3 в окрестности точки х0 = −1.

71.Сформулировать правило Лопиталя.

72.С помощью правила Лопиталя вычислить:

199

ТИПОВЫЕ ВАРИАНТЫ КОНТРОЛЬНЫХ РАБОТ

Контрольная работа № 1

ТЕМА: предел функции, построение эскизов графиков функций. 1. Вычислить:

характер точек разрыва.

Контрольная работа № 2

ТЕМА: дифференцирование функций, вычисление пределов с по- мощью правила Лопиталя, полное исследование функции и построе- ние их графиков.

1. Найти первые производные функций:

200