2004-matematicheskiy-analiz-differencial-noe-ischislenie-funkciy-odnoy-peremennoy-5mb

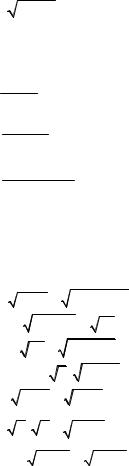
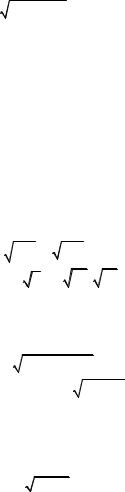
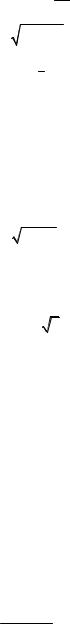Неопределенность вида ∞ − ∞. Умножим числитель и знамена-

Разделим числитель и знаменатель на x:

181

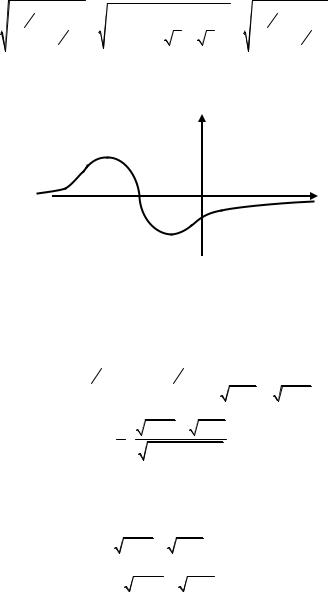
Получили: y = 0 – уравнение горизонтальной асимптоты. 6. Построим эскиз графика функции (рис. 2.22).

Y

Рис. 2.22

Уточним график с помощью первой и второй производной.

7. Найдем точки экстремума и промежутки монотонности функ- ции, для этого найдем первую производную:

=2 3 x + 2 − 3 x + 1 . 3 3 (x + 2)(x + 1)

Найдем точки, в которых производная равна нулю или не существует: y′ = 0;

3x + 2 − 3 x + 1 = 0;

3 x + 2 = 3 x + 1;

x+ 2 = x + 1.

182

Данное уравнение решений не имеет.

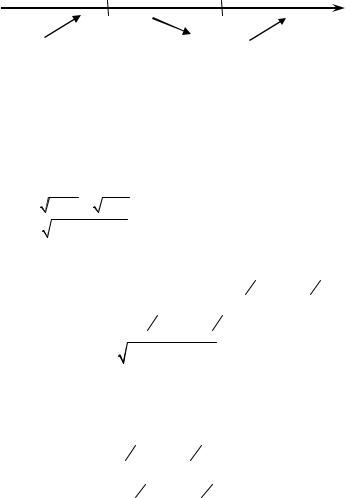
В точках x = –2 и x = –1 производная не существует, следователь- но, x = –2 и x = –1 – критические точки. На числовой прямой отметим критические точки и определим знаки получившихся интервалов:

y(–2) = 1; (–2, 1) – точка максимума функции; y(–1) = –1; (– 1, –1) – точка минимума функции.

На интервалах (−∞, −2) и (−1, ∞) функция возрастает; на интерва- ле (−2, −1) – убывает.

8. Найдем промежутки выпуклости графика функции и точки пе- региба, для этого найдем вторую производную:

Найдем точки, в которых вторая производная равна нулю или не существует:

y′′ = 0;

183

Тогда x = −3/2 – критическая точка второй производной.

Вточках x = –2 и x = –1 производная не существует. Значит x = –2

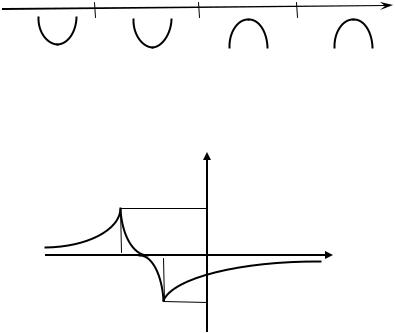
иx = –1 так же являются критическими точками второй производной. На числовой прямой отметим критические точки и определим знаки получившихся интервалов:

На интервалах (−∞, −2) и (−2, −3/2) график функции выпуклый вниз, на интервалах (−3/2, −1) и (−1, ∞) – выпуклый вверх.

y(−3/2) = 0, тогда (−3/2, 0) – точка перегиба. 9. Построим график функции (рис. 2.23).

184

ДОМАШНЕЕ ЗАДАНИЕ

Для получения варианта домашнего задания необходимо, пользу- ясь табл. 1, заполнить пустые клетки табл. 2, затем выписать соот- ветствующие вашему номеру варианта данные из табл. 1. Например, вариант 9.15. По табл. 1 имеем

Вписываем эти буквы в пустые клетки табл. 1 и выбираем строку, соответствующую 15 варианту.

185

Задача 1. Разложить на множители многочлены:

1)(ax + b)2 – (cx + d)2;

2)(ax + b)3 + (cx + d)3.

Задача 2. Решить уравнения:

1)ax + b = cx + d;

2)(x – d) (ax2 + bx + c) = 0;

3)cx + d = f;

Задача 3. Решить неравенства:

1)fx + k > 0;

2)dx + b < f;

3)a(x − b)(x − k)2 ≤ 0 .

(x + c)3 (x − d )

186

Задача 4. Разделить многочлен ax4 + bx3 + cx2 + dx + k на мно-

гочлен bx2 + dx + a .

Задача 5. Построить графики следующих функций, используя графики основных элементарных функций:

1) y = a log2 (x – b);

4) y = f ax − c.

Задача 6. Изобразить на координатной плоскости множество точек, связанных соотношением x2 + ax + y2 + by = 0.

Задача 7. Вычислить пределы функций:

1) lim cx + d ; x→a bx + k

2) lim x2 − f 2 ;

x→ f x3 − f 3

3) lim ax2 + dx + b ; x→∞ cx2 + kx + f

187

20)lim tg(aπx) . x→2 sin(cπx)

Задача 8. Найти асимптоты и построить эскизы графиков функций:

1)y = ax + b ; cx + d

2)y = bx2 + cx + d ; kx + a

3)y = bx2 + cx + d ; kx + a

4)y = bx + a ;

+cdx

188

c2 x2 − d 2

Задача 9. Найти точки разрыва и определить характер разрыва функций:

Задача 10. Найти производные функций:

1) y = ax4 + bx3 + cx2 + d + f в точке х0 = k;

7)y = ( f + 4)x sin (bx);

8)y = sin−b (cx) + k log f (cx − d);

189

12)y = bln tg ax ;

m

13)y = eax + f + c arccos(dx);

14)y = c log1 (arcsin( fx));

Задача 11. Написать уравнения касательной и нормали к графи- кам функций:

1)y = a 3 bx + c в точке х0 = 0;

2)y = ea−bx2 в точке х0 = d.

Задача 12. Используя правило Лопиталя вычислить:

x→0 arctg(dx)

Задача 13. Провести полное исследование и построить графики функций:

1)у = (ax – b)2(cx – d);

=ax3

2)y ; − cx)2(b

190