Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский технологический университет "МИСиС"

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2004-matematicheskiy-analiz-differencial-noe-ischislenie-funkciy-odnoy-peremennoy-5mb

.pdf

Скачиваний:

100

Добавлен:

23.03.2016

Размер:

5.39 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2118 19 20 21 > Следующая >>>

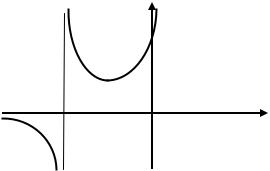
5. Найдем асимптоты функции:

		e2( x+3)		1
lim f (x) = lim			=		= ∞.
lim f (x) = lim			=		= ∞.
x→−3	x→−3 x + 3			0

Следовательно, х = –3 – уравнение вертикальной асимптоты. Наклонную асимптоту определяем по формуле y = kx + b, где

k= lim

f (x)

, b = lim ( f (x) − kx).

x→∞

Правая и левая наклонные асимптоты будут различны.

Правая наклонная асимптота:

e2( x+3)

∞

по правилу

(e2( x+3) )′

k = lim

= lim

x→+∞ x(x + 3)

∞

Лопиталя

x→+∞ (x2 + 3х)′

e2( x+3) (2(x + 3))′

= lim

2e2( x+3)

2x + 3

x→+∞

∞

(e2( x+3) )′

2e2( x+3)

= 2 lim

2 lim

= +∞.

∞

x→+∞ (2x + 3)′

x→+∞

Следовательно, правой наклонной асимптоты нет.

Левая наклонная асимптота:

e2( x+3)

k = lim

lim

x→−∞ x(x + 3)

∞

x→−∞ e−2( x+3) x(x + 3)

∞

b = lim

e2( x+3)

lim

= 0.

+ 3)

x→−∞ (x

∞

x→−∞ e−2( x+3) (x + 3)

∞

Следовательно, y = 0 – уравнение левой горизонтальной асимптоты.

171

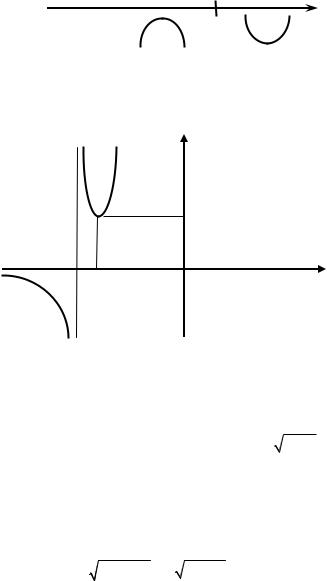
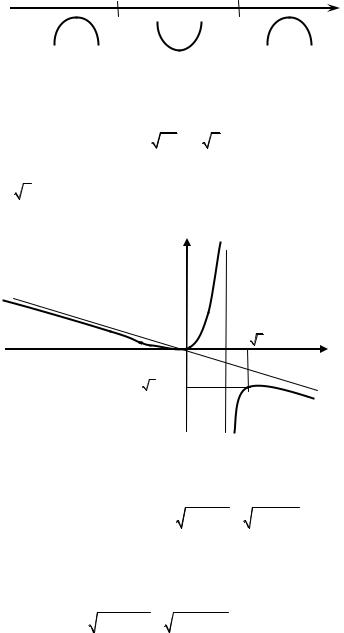
6. Построим эскиз графика функции (рис. 2.18).

−3	О	X
		X

Рис. 2.6.16

Уточним график функции с помощью первой и второй производной. 7. Найдем точки экстремума и промежутки монотонности функ-

ции, для этого найдем первую производную:

y′

e2( x+3) ′

(e2( x+3) )′

(x + 3) − e2( x+3) (x

+ 3)′

(x + 3)2

x +

2e2( x+3)

(x + 3) − e2( x+3)

e2( x+3) (2(x + 3) − 1)

(x + 3)2

+ 3)2

e2( x+3) (2x + 6 − 1)

e2( x+3)

(

2x + 5)

(x + 3)2

3)2

Найдем точки, в которых производная равна нулю:

2x + 5 = 0 x = –5/2.

На числовой прямой отметим нули числителя и нули знаменателя первой производной и определим знаки получившихся интервалов:

172

f ′(x)	−		–					+
f(x)	−3					−5/2		X
							min
В точке, где x = –5/2 – минимум функции;
	y(−5/ 2) =	e2(−5/ 2+3)		=		e	= 2e.
	y(−5/ 2) =	−5/ 2	+ 3	=	1 2		= 2e.
		−5/ 2	+ 3		1 2

На интервалах (–∞, –3) и (−3, −5/2) функция убывает, на интерва- ле (−5/2, ∞) функция возрастает.

8. Найдем промежутки выпуклости графика функции и точки пе- региба, для этого найдем вторую производную:

2(x+3)

(2x +

′

(e2(x+3)

(2x + 5))′ (x + 3)2 − e2(x+3) (2x + 5)((x + 3)2 )′

y′′ =

+ 3)

(x + 3)

(e2(x+3) )′ (2x + 5) + e2(x+3) (2x + 5)′

(x + 3)2 − e2(x+3) (2x + 5)2(x + 3)

(x + 3)4

(2e2( x+3) (2x + 5) + 2e2( x+3) )(x + 3) − 2e2( x+3) (2x + 5)

(x + 3)3

2e2(x+3) ((

2x + 5 +1)(x + 3) − (2x + 5))

2e2(x+3) ((2x + 6)(x + 3) − 2x − 5)

(x + 3)3

2e2( x+3) (2x2 + 6x + 6x + 18 − 2x − 5)

2e2( x+3)

(2x2

+ 10x + 13)

(x + 3)3

(x +

3)3

Найдем точки, в которых вторая производная равна нулю: е2(х+3) > 0 для любого x, следовательно, 2x2 + 10x + 13 = 0;

D = 100 – 8 13 = 100 – 104 < 0 – корней нет, а значит, числитель не равен нулю ни при каких значениях x.

173

На числовой прямой отметим ноль знаменателя и определим зна- ки получившихся интервалов:

f ′′(x)	−		+
f(x)		−3	X

На интервале (–∞, –3) график функции выпуклый вверх, на интер- вале (–3, ∞) график выпуклый вниз.

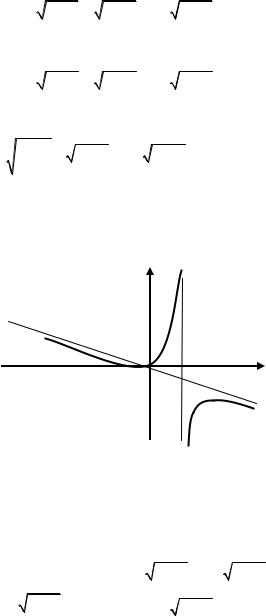
9. Построим график функции (рис. 2.19).

			2e
−3	−5/2	О	X
		О

Рис. 2.19

Пример 2.6.6

Провести полное исследование функции y = −	x2
		и постро-

	23 x3 − 1

ить график.

Решение

1.Область определения функции: x (–∞, 1) (1, ∞).

2.Функция не является ни четной, ни нечетной, так как

	− (− x)2		− x2
y(− x) =		=		≠ ± y(x).

23 (− x)3 − 1 23 − x3 − 1

174

3. Найдем точки пересечения с осями координат.

Пусть х = 0, тогда у = 0. Значит, (0, 0) – точка пересечения с осями координат.

4. Найдем промежутки постоянства знака значений функции.

На числовой прямой отметим нули числителя и нули знаменателя функции и определим знаки получившихся интервалов:

+	+	–
0	1	X

5. Найдем асимптоты функции:
lim	− x2	= −∞; lim	− x	2	= +∞.

x→1+0 23 x3 − 1		x→1−0 23 x3 − 1

Следовательно, x = 1 – уравнение вертикальной асимптоты. Наклонную асимптоту определим по формуле y = kx + b, где

k= lim

f (x)

, b = lim ( f (x) − kx).

x→∞

Тогда

k = lim

− x2

= lim

− x

= lim

−1

= −

;

3 x3 − 1

x→∞ 23 x3 − 1 x

x→∞ 2

x→∞

−

3 1

− x

− x2 + x 3 x3 − 1

x(3 x3 − 1 − x)

b = lim

= lim

3 x3 − 1

x→∞

23 x3 − 1

x→∞

23 x3 − 1

x→∞ 2

Неопределенность вида ∞ − ∞. Умножим числитель и знаменатель на выражение, сопряженное к числителю, т.е. на 3 (x3 −1)2 + x3 x3 −1 + x2 :

x(3

(3 x3 − 1)

+ x 3

x3 − 1 + x2

x3 − 1 − x)

lim

(3 x3

− 1)

x→∞

x3 − 1

+ x 3 x3

− 1 + x2

175

= lim			x(x3 − 1− x3 )				=

			(3 x3 − 1)	2
x→∞	3	x3 − 1		2	+ x 3 x3	− 1 + x2
2	3	x3 − 1			+ x 3 x3	− 1 + x2

= lim			− x				=
= lim			(3 x3 − 1)	2			=
x→∞	3	x3 − 1		2	+ x 3 x3	− 1 + x2
2	3	x3 − 1			+ x 3 x3	− 1 + x2

= lim				−1			= −1	= 0.
= lim		1					= −1	= 0.
x→∞		1			2		∞
	23 1−		(3 x3 − 1)		2	+ x 3 x3 − 1 + x2

		3
		х

Получили: y = −x/2 – уравнение наклонной асимптоты. 6. Построим эскиз графика функции (рис. 2.20).

y = −x/2

	О	1
	О	X
		X

Рис. 2.20

ции, для этого найдем первую производную:

		x	2	′	1	(x2 )′ 3 x3 − 1 − x2 (		3 x3 − 1)′
y′ = −				= −		(3 x3 − 1)		=
							2
	3				2
2		x3 − 1

176

2x 3

x3 −1 − x2

(x3 −1)−2 / 3 3x2

= −

(3 x3 −1)2

1 2x 3

x3 − 1 − x4 (x3

− 1)−2 / 3

1 (x3

− 1)−2 / 3 (2x(x3 − 1)− x4 )

= −

(3 x3 − 1)2

= −

1 (2x4 − 2x − x4 )

= −

x4 − 2x

(x3 − 1)4

2 3

23 (x3 − 1)4

Найдем точки, в которых производная равна нулю или не существует:

y' = 0 x = 0 или x = 3 2;

х ≠ 1.

f ′(x)	–	+	+	−
f(x)		0	1	3 2	X
		min		max
В точке, где x = 0 – минимум функции, у(0) = 0.
В точке, где x =		3 2 – максимум функции,		y(3 2) = − 3 4 .
				2

На интервалах (–∞, 0) и ( 3 2 , ∞) функция убывает, на интервалах

(0, 1) и (1, 3 2 ) функция возрастает.

8. Найдем промежутки выпуклости и точки перегиба, для этого найдем вторую производную функции.

177

− 2)

′

−

′

x(x

y′′ =

−

= −

23 (x3 − 1)4

(x3 − 1)4

(x4 − 2х)′ 3 (x3 − 1)4 − (x4 − 2х) 3

(x3 − 1)4 ′

= −

3 (x3 − 1)8

(4x3

− 2)3 (x3 − 1)4 − (x4 − 2х)

(x3 − 1)

3x2

= −

3 (x3 − 1)8

1 (4x3 − 2)(x3 − 1)

− 4(x4 − 2х)(x3 − 1)

= −

3 (x3 − 1)8

((4x3 − 2)(x3 − 1)− 4(x4 − 2х)x2 )

1 (x3

− 1)

= −

3 (x3 − 1)8

= −

2((2x3 − 1)(x3 − 1)− 2(x4 − 2х)x

2 )

3 (x3 − 1)7

= −

2x6 − x3 − 2x3 + 1− 2x6 + 4x3

= −

x3 + 1

3 (x3 − 1)7

Найдем точки, в которых вторая производная равна нулю:

x3+1 = 0 x = –1.

На числовой прямой отметим нули числителя и нули знаменателя второй производной и определим знаки получившихся интервалов.

178

f ′′(x)	−	+		−
f(x)		−1	1	X

На интервалах (–∞, –1) и (1, ∞) график функции выпуклый вверх, на интервале (–1, 1) график функции выпуклый вниз.

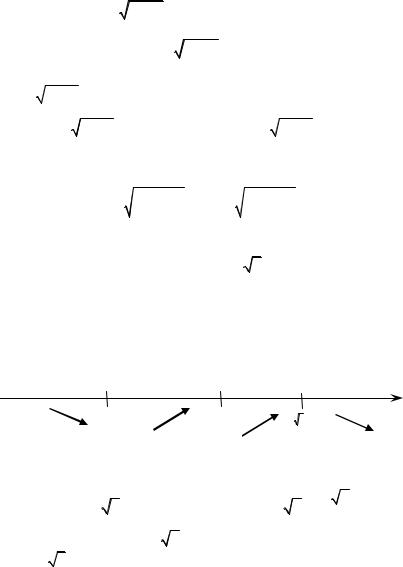
В точке, где х = –1 – перегиб функции,

y(−1) =	−1	=	1	;
			23 2
	23 −2

−1,	1		− точка перегиба .
	23
		2

9. Построим график (рис. 2.21).

y = −x/2

			− 3 4 / 2
−1	О	1	X
	О		X
− 3 4 / 2

Рис. 2.21

Пример 2.6.7

Построить график функции y = 3 (x + 1)2 − 3 (x + 2)2 с полным ис- следованием.

Решение

1.Область определения функции: x R.

2.Функция не является ни четной, ни нечетной, так как

y(− x) = 3 (− x + 1)2 − 3 (− x + 2)2 ≠ ± y(x).

179

3. Найдем точки пересечения с осями координат.

Пусть x = 0, тогда y = 1− 3 4 . Следовательно, (0, 1 − 3 4 ) – точка

пересечения с осью OY. Пусть y = 0, тогда

3(x + 1)2 − 3 (x + 2)2 = 0;

3 (x + 1)2 = 3 (x + 2)2 ;

x + 1 = x + 2,

(x + 1)2 = (x + 2)2 x + 1 = − x − 2 x = −3/ 2.

Тогда (−3/2, 0) – точка пересечения с осью OX.

4. Найдем промежутки постоянства знака значений функции.

На числовой прямой отметим нули числителя и определим знаки получившихся интервалов:

f(x)

–

−3/2

5. Найдем асимптоты.

Вертикальных асимптот нет. Наклонную асимптоту определим по формуле y = kx + b, где

k= lim		f (x)		; b = lim		( f (x) − kx).

x→∞			x		x→∞
Тогда
	f (x)				3 (x + 1)2 −		3 (x + 2)2
k = lim			= lim					=
						x
x→∞ x			x→∞

= lim 3 (x + 1)2

x→∞ x

= lim

x→∞

b = lim( f

x→∞

(x + 2)2

(x + 1)2

(x + 2)2

− lim

= lim 3

− lim 3

x→∞

− 3

= 0 − 0 = 0;

x x2

(x) − kx) = lim

(3 (x + 1)2

− 3 (x + 2)2 − 0 x).

x→∞

180

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2118 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.04.20254.15 Mб12-2-Учебное пособие-ЭЭ и ОВОС.doc
#
01.04.2025963.58 Кб12-3-Курс лекций-ЭЭ и ОВОС.doc
#
20.04.201532.07 Кб362. Классификация материалов.doc
#
01.04.202539.55 Кб12.таможенно-тарифное регулирование.docx
#
27.09.201947.1 Кб1120-24.doc
#
23.03.20165.39 Mб1002004-matematicheskiy-analiz-differencial-noe-ischislenie-funkciy-odnoy-peremennoy-5mb.pdf
#
23.03.20162.95 Mб3262006-matematicheskiy-analiz-differencial-nye-uravneniya-2mb.pdf
#
13.09.201964.51 Кб162012-Вопросы по теоретической механике.doc
#
01.05.2025418.82 Кб02013-07-18_Uchebnik_dlya_marshalov.docx
#
01.05.2025955.39 Кб02014_Билеты для госэкзамена.doc
#
23.03.201626.97 Mб77203-elektrotehnika-i-elektronika-elektronika-26mb.pdf