2004-matematicheskiy-analiz-differencial-noe-ischislenie-funkciy-odnoy-peremennoy-5mb

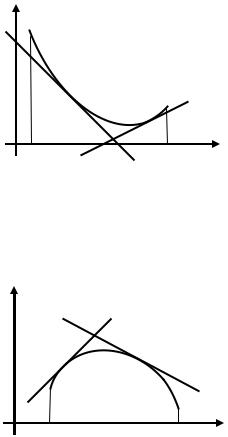
2. Второй достаточный признак экстремума.

Пусть в точке x0 функция имеет первую и вторую производную. Точка x0 есть точка экстремума функции y = f(x), если f ′(x0) = 0,

аf ′′(x0) ≠ 0, причем,

–если f ′′(x0) > 0, то x0 − точка локального минимума,

–если f ′′(x0) < 0, то x0 − точка локального максимума.

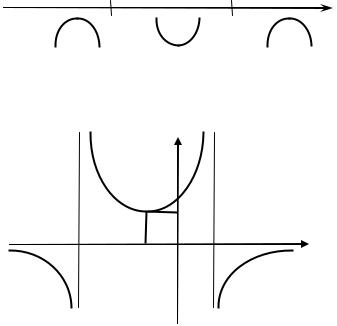
Выпуклость графика функции

График функции y = f(x) выпукл вниз на интервале (а, b), если на этом интервале дуга кривой расположена выше касательной, прове- денной в любой точке этого интервала (рис. 2.7).

Y

y = f(x)

Рис. 2.7

График функции y = f(x) выпукл вверх на интервале (а, b), если ду- га кривой на этом интервале расположена ниже касательной, прове- денной в любой точке этого интервала (рис. 2.8).

Y

y = f(x)

151

Достаточные условия выпуклости

Пусть функция y = f(x) имеет первую и вторую производную на интервале (а, b). Тогда:

а) если f ′′(x) ≤ 0 для любого x (а, b), то график функции выпукл вверх;

б) если f ′′(x) ≥ 0 для любого x (а, b), то график функции выпукл вниз.

Точки перегиба

Точка P(х0, f(x0)) называется точкой перегиба графика функции у = f(x), если в этой точке график имеет касательную и существует окрестность точки х0 оси ОХ, в пределах которой слева и справа от х0 график функции имеет разные направления выпуклости (рис. 2.9).

Y

P

f(x0)

Рис. 2.9

Необходимое условие точки перегиба

Точка x0 может быть точкой перегиба, если в этой точке вторая производная равна нулю или не существует.

Достаточный признак точки перегиба

1. Первый достаточный признак точки перегиба.

Пусть функция y = f(x) непрерывна в точке x0 и имеет вторую про- изводную в некоторой окрестности этой точки. Если при переходе через точку x0 вторая производная меняет знак, то точка x0 является точкой перегиба.

2. Второй достаточный признак точки перегиба.

Пусть функция y = f(x) непрерывна в точке x0 и имеет вторую произ- водную в некоторой окрестности этой точки. Если f ′′(x0) = 0, а f ′′′ (x0) ≠ 0, то точка x0 является точкой перегиба.

152

План построения графика функции

1.Найти область допустимых значений.

2.Определить, является ли функция четной или нечетной.

3.Определить, является ли функция периодической или общего вида.

4.Найти точки пересечения с осями координат.

5.Найти промежутки постоянства знака значений функции.

6.Найти асимптоты функции.

7.Нарисовать эскиз графика функции.

8.Найти экстремумы функции и промежутки монотонности.

9.Найти промежутки выпуклости функции и точки перегиба.

10.Найти дополнительные точки.

11.Построить график функции.

Наибольшее и наименьшее значения функции на отрезке

Наибольшее (наименьшее) значение непрерывной функции y = f(x)

на отрезке [a, b] достигается либо в критических точках этого отрез- ка, либо на концах отрезка.

Чтобы найти наибольшее (наименьшее) значение функции f(x) на отрезке [a, b], надо:

1)найти f ′(x);

2)найти критические точки, т.е. точки, в которых f ′(x) = 0 или не существует;

3)среди получившихся точек выбрать те, которые принадлежат отрезку [a, b];

4)найти значение функций в выбранных точках и на концах отрезка;

5)cреди получившихся значений выбрать наибольшее и наи- меньшее.

Пример 2.6.1

Провести полное исследование функции y = (x + 1)2(2x – 3) и по- строить график.

Решение

1.Область определения функции – вся числовая ось.

2.Функция не является ни четной, ни нечетной, так как

y(–x) = ((–x) + 1)2(2(–x) – 3) = (–x + 1)2(–2x – 3) ≠ ±y(x).

3. Найдем точки пересечения с осями координат.

С осью OY график пересекается при x = 0, тогда y = –3, т.е. (0, –3) – точка пересечения с осью OY;

153

С осью OX график пересекается при y = 0, тогда x = –1 или x = 3/2, т.е. (–1, 0) и (3/2, 0) – точки пересечения с осью OX.

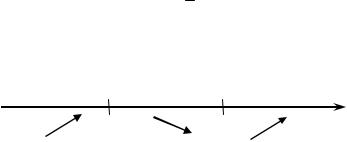
4. Найдем промежутки постоянства знака значений функции. На числовой прямой отметим нули функции и определим знаки полу- чившихся интервалов:

Следовательно, на интервалах (−∞, −1) и (−1, 3/2) график функции расположен ниже оси OX, а на интервале (3/2, + ∞) − выше оси OX.

5. Найдем асимптоты функций.

Функция является непрерывной, следовательно, вертикальных асимптот нет. Наклонных асимптот нет, так как

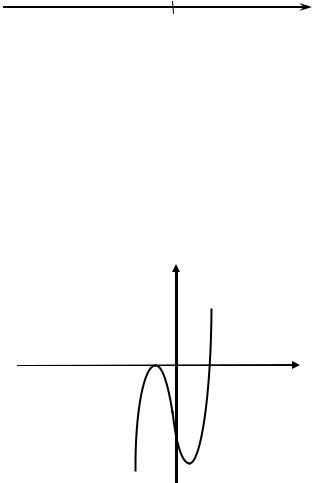
6. Построим эскиз графика функции (рис. 2.10).

Y

−1

−3

Рис. 2.10

Уточним график с помощью первой и второй производной.

7. Найдем точки экстремума и промежутки монотонности функции:

154

y′ = ((x + 1)2 (2x − 3))′ = ((x + 1)2 )′ (2x − 3) + (x + 1)2 (2x − 3)′ =

= 2(x + 1)(2x − 3) + (x + 1)2 2 = 2(x + 1)(2x − 3 + x + 1) = 2(x + 1)(3x − 2).

Найдем нули производной:

y' = 0, тогда 2(x + 1)(3x – 2) = 0;

x + 1 = 0 или 3x – 2 = 0;

x = –1, x = 2 .

3

На числовой оси отметим нули первой производной и определим знаки получившихся интервалов:

Найдем значения функции в точках экстремума:

у(–1) = 0,

Тогда в точке (–1, 0) – максимум функции, в точке (2/3, –125/27) – минимум функции. На интервалах (−∞, −1) и (2/3, ∞) функция воз- растает; на интервале (−1, 2/3) функция убывает.

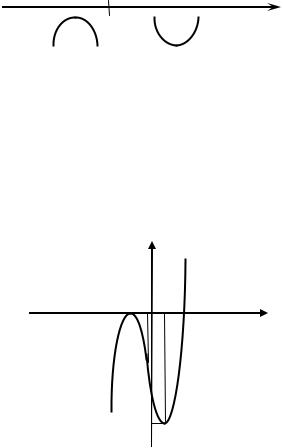
8. Найдем промежутки выпуклости графика функции и точки пе- региба:

y′′ = (2(x + 1)(3x − 2))′ = 2(x + 1)′ (3x − 2) + 2(x + 1)(3x − 2)′ = = 2(3x − 2) + 2(x + 1) 3 = 6x − 4 + 6x + 6 = 12x + 2.

Найдем нули второй производной:

155

12x + 2 = 0 x = −1/ 6.

Отметим нули второй производной на числовой прямой и опреде- лим знаки получившихся интервалов:

ванием.

156

Решение

1. Найдем область определения функции:

3 − 2x − x2 ≠ 0;

x2 + 2x − 3 ≠ 0;

x ≠ 1 и x ≠ −3.

D( f ) = (−∞, −3) (−3, 1) (1, ∞).

2. Функция не является ни четной, ни нечетной, так как

осью OY. Точек пересечения с осью OX нет.

4. Найдем промежутки постоянства знака значений функции.

На числовой прямой отметим нули числителя и нули знаменателя функции и найдем знаки получившихся интервалов:

Следовательно, на интервалах (−∞, −3) и (1, ∞) график функции расположен ниже оси OX, а на интервале (−3, 1) − выше оси OX.

5. Найдем асимптоты:

157

Следовательно, x = 1 и x = –3 – уравнения вертикальных асимптот. Наклонную асимптоту определяем по формуле y = kx + b, где

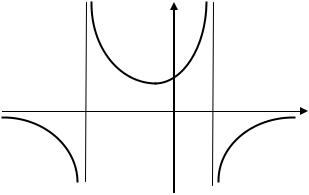
Тогда y = 0 – уравнение горизонтальной асимптоты. 6. Построим эскиз графика функции (рис. 2.12).

Y

−3 1

Рис. 2.12

Уточним график с помощью первой и второй производной.

7. Найдем точки экстремума и промежутки монотонности, для этого найдем первую производную:

Найдем нули числителя:

8 + 8x = 0 x = −1 – критическая точка.

158

На числовой прямой отметим точки, в которых первая производ- ная равна нулю или не существует, и определим знаки получившихся интервалов:

Найдем значения функции в точках экстремума:

Тогда в точке (–1, 1) – минимум функции; на интервалах (−∞, −3) и (−3, −1) функция убывает, на интервалах (−1, 1) и (1, ∞) функция возрастает.

8. Найдем промежутки выпуклости графика функции и точки пе- региба, для этого найдем вторую производную:

=8(3x2 + 6x + 7). (3 − 2x − x2 )3

Найдем нули числителя:

159

3x2 + 6x + 7 = 0 ;

D = 36 − 4 21 < 0 корней нет.

На числовой прямой отметим нули знаменателя и определим зна- ки получившихся интервалов:

На интервалах (−∞, −3) и (1, ∞) график функции выпуклый вверх, на интервале (–3, 1) – выпуклый вниз.

9. Построим график функции (рис. 2.13).

Y

Рис. 2.13

Пример 2.6.3

160