2004-matematicheskiy-analiz-differencial-noe-ischislenie-funkciy-odnoy-peremennoy-5mb

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский технологический университет "МИСиС"

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

(2x)′ ln x + arctg(2x)

= xarctg(2x)

.pdf

Скачиваний:

101

Добавлен:

23.03.2016

Размер:

5.39 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2111 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Пример 2.1.12
Найти производную функции y = ln tg	−	x	.

		8

Решение

Воспользуемся правилом нахождения производной сложной функции:

(f(g(x))' = f ' (g(x))g'(x),

а также нечетностью функции y = tg x и четностью функции y = cos x. Тогда

y′ =

′

x ′

−

cos

−

= −

−

cos

−

−8tg

cos

8tg

cos

Пример 2.1.13

e− x + 2 + 2arccos(3x).

Найти производную функции y =

Решение

По правилу дифференцирования сложной функции

′

y′ =

− x

2) +

2 e

− x

+ 2

−

(3x)

(3x)′ =

1−

(e− x (− x)′ +

0)−

2 3

1− 9x2

2 e− x + 2

e− x (−1) −

= −

e− x

−

2 e− x + 2

1− 9x2

2 e− x + 2

1− 9x2

Пример 2.1.14

Найти производную функции y = 2log1 (arcsin (2x)) .

101

Решение

По правилу дифференцирования сложной функции

1 (arcsin (2x))

′

(arcsin (2x))′ =

y′ = 2 log

= 2

arcsin (2x)ln

(2x)′ =

−

(2x)

arcsin (2x)ln

1− 4x

Пример 2.1.15

( x−1)2

ctg

Найти производную функции y = 3

Решение

По правилу дифференцирования сложной функции

( x−1)

′

ctg

y′ =

− 1)

ln3 ctg

( x−1)

′

ctg

= 3

ln 3

−

(x − 1)

sin

( x−1)

′

ctg

ln 3

− 1)

= −3

(x − 1)2 3

sin

( x−1)

′

ctg

ln3

1 ((x − 1)

)

x − (x − 1)

x′

= −3

sin

(x − 1)2

102

( x−1)2

ctg

ln 3

2(x − 1)(x − 1)' x − (x −

= −3

sin

(x − 1)2

3x2

( x−1)2

ctg

ln 3

2(x − 1)x −

(x − 1)

= −3

sin

(x − 1)2

3x2

(x−1)2

ctg

ln3

(x −1)(2x − x +1)

ctg

−1)ln3 .

= −3

sin

(x −1)2

3x2

sin

(x −1)2

Пример 2.1.16

Найти производную функции y = xarctg(2x) .

Решение

Данная функция не является ни показательной, ни степенной. По- этому для нахождения производной этой функции воспользуемся формулой

y′ = y(ln y)′.

Тогда

y′ = xarctg(2x) (ln xarctg(2x) )′ = xarctg(2x) (arctg(2x)ln x)′ =

= xarctg(2x) ((arctg(2x))′ ln x + arctg(2x)(ln x)′ )=

103

Пример 2.1.17

		1	2 x+3
Найти производную функции	y =		− 1 .

	x

Решение

Функция не является ни показательной, ни степенной. Поэтому для нахождения производной этой функции воспользуемся формулой

y′ = y(ln y)′.

Тогда

2 x+3

2x+3

′

2 x+3

′

y′ =

− 1

(2x + 3)ln

− 1

2 x+3

′

−

(2x

+ 3)′ ln

− 1

+ (2x + 3) ln

− 1

′

2x+3

−

2ln

−

+ (2x + 3)

− 1

2 x+3

− 1

2ln

− 1

+ (2x +

−

− x

2 x+3

2x +

− 1

2ln

− 1

−

− x

Пример 2.1.18

Написать уравнение касательной и уравнение нормали к графику функции y = − 3 x + 2 в точке с абсциссой х0 = 0.

Решение

Уравнение касательной:

y = f(x0) + f '(x0)(x – x0).

Уравнение нормали:

(x – x0) + f '(x0)(y – f(x0)) = 0.

104

Найдем значение функции в точке х0 = 0:

			f (x ) = f (0) = − 3 2.
				0
Найдем производную:
f ′(x) = (− 3 x + 2 )′ = − (x + 2)							3					= − 1 (x + 2)3−1									= − 1 (x + 2)− 3 .
							1			′							1						2

															3						3
Тогда значение производной в точке х0 = 0
f ′(x		) = f ′(0) = −									1		2−				2		1
											1						3	= −	1	.
																	3	= −		.
0									3								33 4
									3								33 4
Запишем уравнение касательной:
	y = − 3			2 +				−				1					(x − 0);


										33 4
			y = − 3 2 −											x				.
			y = − 3 2 −															.
												33 4
Запишем уравнение нормали:
						1
	x − 0 +			−								( y		+ 3 2) = 0;
	x − 0 +			−								( y		+ 3 2) = 0;
				33				4
			x −		y			−				3 2				= 0;

				33 4
				33 4					33 4
			x −		y			−				1				= 0.
			x −	33 4				−								= 0.
				33 4					33 2
Итак, y = − 3 2 −	x		– уравнение касательной;																		x −	y	−	1	= 0 –
Итак, y = − 3 2 −			– уравнение касательной;																		x −		−		= 0 –
33 4																					33 4		33 2

уравнение нормали к графику функции y = − 3 x + 2 в точке с абс- циссой х0 = 0.

105

Пример 2.1.19

Написать уравнение касательной и уравнение нормали к графику функции y = e1− x2 в точке с абсциссой х0 = −1.

Решение

Уравнение касательной:

y = f(x0) + f '(x0)(x – x0).

Уравнение нормали:

(x – x0) + f '(x0)(y – f(x0)) = 0.

Найдем значение функции в точке х0 = −1:

f (x0 ) = f (−1) = e1−(−1)2 = e0 = 1.

Найдем производную:

f ′(x) = (e1− x2 )′ = e1− x2 (1− x2 )′ = e1− x2 (−2x).

Тогда значение производной в точке х0 = −1

f ′(x0 ) = f ′(−1) = −2(−1)e1−(−1)2 = 2e0 = 2.

Запишем уравнение касательной:

y = 1 + 2(x + 1); y = 2x + 3.

Запишем уравнение нормали:

(x + 1) + 2(y – 1) = 0; x + 1 + 2y – 2 = 0.

Итак, y = 2x + 3 – уравнение касательной, x + 2y – 1 = 0 – уравне- ние нормали к графику функции y = e1− x2 в точке с абсциссой х0 = −1.

106

2.2. Дифференциал функции. Дифференцируемость функции

Пусть функция y = f(x) определена в некоторой окрестности точки

х0, а приращение ∆y = f(x0 + ∆x) – f(x0) функции f(x) в точке х0 можно представить в виде

y = A x + o( x),

где А − некоторое число, которое не зависит от ∆x; o(∆x) → 0 при ∆x → 0. Тогда функция f(x) называется дифференцируемой в точке х0, а произведение A∆x называется ее дифференциалом в точке х0 и обо- значается df(х0).

Для того чтобы функция y = f(x) была дифференцируемой в точке х0, необходимо и достаточно, чтобы эта функция имела производную в этой точке.

Если функция дифференцируема в точке х0, то ее дифференциал в этой точке

dy = y′(x0) ∆x.

Для функции y = x имеем dy = ∆x, т.е. дифференциал независимо- го переменного x совпадает с приращением ∆x. Поэтому дифферен- циал функции y = f(x) записывается в виде

dy = y′(x0)dx,

и производная y ′ может быть записана как отношение дифференциалов:

y′ = dy . dx

Основные правила вычисления дифференциалов функций те же, что и для вычисления производной:

1)dc = 0, где c = const;

2)d (αf + βg) = αdf + βdg;

3)d ( fg) = g df + fdg;

4) d	f	=	gdf − fdg	(g(x) ≠ 0);
			g2
	g

5) d ( f (u)) = f ′(u)du.

Функция, дифференцируемая в каждой точке некоторого интерва-

ла, называется дифференцируемой на этом интервале. Производная дифференцируемой на интервале функции y = f(x) сама является функцией аргумента x.

107

Связь между непрерывностью и дифференцируемостью

Если функция y = f(x) дифференцируема в точке х0, то она непре- рывна в этой точке. Обратное заключение неверно: из непрерывно- сти функции в точке х0 не следует дифференцируемость функции в этой точке.

Например, функция y = x непрерывна в точке х0 = 0, но она не дифференцируема в этой точке, так как

f ′(0) = lim

f (0 +

x) − f (0)

= lim

− 0

= lim

x = 1;

x→0+0

x→0+0 x

f ′(0)

= lim

f (0 +

x) − f (0)

lim

− 0

lim −

x = −1.

−

x→−0

x→0−0

x→0+0

Левая и правая производные не равны между собой. Следователь- но, в точке х0 = 0 функция y = х не имеет производной.

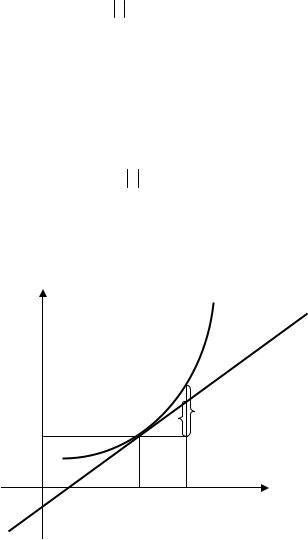
Геометрический смысл дифференциала

Дифференциал функции в точке M0(х0, y0) равен приращению ор- динаты касательной к графику этой функции в точке с абсциссой х0 при изменении аргумента от х0 до х0 + ∆x (рис. 2.2).

y = f(x)

М0 dy

x0+ x

Рис. 2.2

108

Применение дифференциала функции к приближенным вычислениям

Если приращение ∆x → 0, то дифференциал dy функции y = f(x) и приращение ∆y приближенно равны между собой:

y ≈ dy f (x0 + x) − f (x0 ) ≈ f ′(x0 ) x f (x0 + x) ≈ f (x0 ) + f ′(x0 ) x.

Пример 2.2.1

Найти дифференциал функции y = x 5ln sin x .

Решение

Для нахождения дифференциала воспользуемся формулой

dy = y ′(x)dx.

Найдем производную заданной функции, применив формулу для нахождения производной произведения

(uv)′ = u′v + uv′,

и правило нахождения производной сложной функции:

(f(g(x))' = f '(g(x))g '(x).

y′ = ( x 5ln sin x )′ = ( x)′ 5ln sin x +

x (5ln sin x )′ =

5ln sin x +

x 5ln sin x ln 5(ln sin x)′ =

5ln sin x +

x 5ln sin x ln 5

(sin x)′ =

5ln sin x

x 5ln sin x ln 5cos x

sin x

2 x

sin x

Тогда

dy = 5	ln sin x	1	+
				x ln 5ctg x dx.

	2	x

Пример 2.2.2

Найти дифференциал функции y = (1+ tg x)arcsin2 x .

Решение

Дифференциал функции y(x): dy = y ′(x)dx.

109

Найдем производную заданной функции. Функция y = (1+ tg x)arcsin2 x не является ни показательной, ни степенной. По-

этому для нахождения производной этой функции воспользуемся формулой

y′ = y(ln y)′.

Тогда

y′ = y(ln(1+ tg x)arcsin2 x )′ = (1+ tg x)arcsin2 x (arcsin2 x ln(1+ tg x))′.

По формуле для нахождения производной произведения и по пра- вилу дифференцирования сложной функции имеем:

y′ = (1+ tg x)arcsin2 x ((arcsin2 x)′ ln(1+ tg x) + arcsin2 x(ln(1+ tg x))′) =

= (1+ tg x)arcsin

2arcsin x(arcsin x)′ln(1+ tg x) + arcsin2 x

(1+ tg x)′

1+ tg x

= (1+ tg x)

arcsin2 x

2arcsin х ln(1+ tg x)

arcsin2

1− x2

(1+ tg x)cos

Тогда

dy = (1+ tg x)	arcsin2 x	2arcsin х ln(1+ tg x)	+	arcsin2	x
								dx.
						2		dx.
		1− x2		(1+ tg x)cos		2
		1− x2		(1+ tg x)cos			x

Пример 2.2.3

Вычислить приближенно с помощью дифференциала 0,99819.

Решение

Рассмотрим функцию y = x19. В формуле f(x0 + ∆x) ≈ f(x0) + f ′(x0)∆x

положим x0 = 1, тогда ∆x = 0,998 − 1 = −0,002.

Найдем значение функции y = x19 и значение производной в точке x0 = 1:

y(1) = 119 =1;

y ′ (x) = 19x18 ;

y ′ (1) = 19.

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2111 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.04.20251.17 Mб12-1-Пособия-ЭЭ и ОВОС.doc
#
01.04.20254.15 Mб12-2-Учебное пособие-ЭЭ и ОВОС.doc
#
01.04.2025963.58 Кб12-3-Курс лекций-ЭЭ и ОВОС.doc
#
20.04.201532.07 Кб362. Классификация материалов.doc
#
27.09.201947.1 Кб1120-24.doc
#
23.03.20165.39 Mб1012004-matematicheskiy-analiz-differencial-noe-ischislenie-funkciy-odnoy-peremennoy-5mb.pdf
#
23.03.20162.95 Mб3272006-matematicheskiy-analiz-differencial-nye-uravneniya-2mb.pdf
#
13.09.201964.51 Кб162012-Вопросы по теоретической механике.doc
#
01.05.2025418.82 Кб02013-07-18_Uchebnik_dlya_marshalov.docx
#
01.05.2025955.39 Кб22014_Билеты для госэкзамена.doc
#
23.03.201626.97 Mб79203-elektrotehnika-i-elektronika-elektronika-26mb.pdf