
2004-matematicheskiy-analiz-differencial-noe-ischislenie-funkciy-odnoy-peremennoy-5mb
.pdf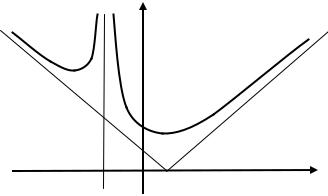
|
|
|
|
|
|
|
x2 |
|
|
+ |
1 |
|
+ |
5 |
|
|||||
|
|
|
|
2 |
+ x + 5 |
|
1 |
|
|
|
|
|
|
|
||||||
|
f (x) |
|
x |
|
x |
|
x |
2 |
||||||||||||
k = lim |
= lim |
|
= lim |
|
|
|
|
|
|
|
|
|
= 1; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x→+∞ |
x |
x→+∞ |
x(x + 2) x→+∞ |
|
|
2 |
|
|
+ |
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
x |
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||
b = lim |
( f (x) − kx) = lim |
x2 + x + 5 |
− x = |
|||||||
|
||||||||||
|
x→+∞ |
|
|
x→+∞ |
x + 2 |
|
|
|
||
= |
|
x2 |
+ x + 5 − x2 |
− 2x |
= |
− x + 5 |
= −1. |
|||
lim |
|
|
|
|
lim |
|
|
|||
|
|
x + 2 |
|
+ 2 |
||||||
|
x→+∞ |
|
|
|
x→+∞ x |
|
||||
Следовательно, y = x – 1 – уравнение правой наклонной асимптоты. Найдем левую наклонную асимптоту:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
+ |
1 |
|
+ |
|
5 |
|||||||
|
|
|
|
|
|
|
2 |
+ x + 5 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
|
f (x) |
|
|
x |
|
|
|
|
|
x |
|
|
x |
2 |
||||||||||||||
k = lim |
|
= lim |
|
= − lim |
|
|
|
|
|
|
|
|
|
|
|
= −1; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x→−∞ |
|
|
x |
x→−∞ − x(x + 2) |
x→−∞ |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
1+ |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||
b = lim |
( f (x) − kx) = lim − |
x2 + x + 5 |
+ x = |
|
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
x→+∞ |
|
|
|
x→+∞ |
|
|
|
x + 2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
= |
|
− x2 − x − 5 + x2 + 2x |
= |
|
|
|
x − 5 |
= 1. |
|
|
|
|||||||||||||||||
|
lim |
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
x + 2 |
|
|
|
|
+ |
2 |
|
|
|
|
||||||||||||||||
|
|
|
x→+∞ |
|
|
|
|
|
x→+∞ x |
|
|
|
|
|
|
|
|
|
|||||||||||
Следовательно, y = −x + 1 – уравнение левой наклонной асимптоты. 7. Построим эскиз графика функции (рис. 1.47).
Y
y = 1 − x
y = x − 1
−2 |
1 |
X |
Рис. 1.47
91
2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
2.1. Производная функции, ее геометрический смысл
Пусть функция f(x) определена в некоторой окрестности U(x0) точки x0. Тогда для любой точки x U(x0) разность x − x0 обозначает- ся ∆x и называется приращением аргумента. Соответствующая раз- ность значений функции f(x) – f(x0) обозначается ∆f(x0) и называется
приращением функции. Так как x = x0 + ∆x, то ∆f(x0) = f(x0 + ∆x) – f(x0).
Производной функции y = f(x) в точке х0 называется предел отно- шения приращения функции f(x0, x) к соответствующему прира- щению аргумента x, если приращение аргумента стремится к нулю:
f ′(x ) = lim |
f (x0 , |
x) |
= lim |
f (x0 + |
x) − f (x0 ) |
. |
|
|
|
|
|
||||
0 |
x→0 |
x |
|
x→0 |
x |
||
|
|
||||||
Геометрический смысл производной
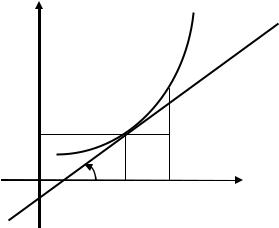
Рассмотрим график некоторой функции y = f(x), непрерывной на интервале (a, b) (рис. 2.1).
Y
y = f(x)
N
М0
y0
ϕ
O |
x0 x0 + x |
X |
Рис. 2.1
92

Пусть точки M0(x0, f(x0)), N(x0 + ∆x, f(x0 + ∆x)) − произвольные точ- ки, лежащие на кривой y = f(x) (a < x0 < b). Прямая M0N называется
f (x0 + x) − f (x0 )
x
енту прямой, проходящей через точки M0 и N. Пусть x → 0, тогда точка N стремится к точке M0. Если существует производная f ′(x0),
т.е. существует предел отношения f (x0 + x) − f (x0 ) , то секущая M0N x
стремится к прямой, проходящей через точку M0 с угловым коэффи- циентом f ′(x0). Предельное положение секущей M0N при стремлении N к M0 называется касательной к графику функции y = f(x) в точке M0.
Значение производной функции f(x) в точке x0 равно угловому коэф- фициенту касательной, проведенной к графику функции в этой точке:
f ′(x0) = k = tg ϕ.
Тогда y – f(x0) = f ′(x0)(x – x0) – уравнение касательной к графику
функции y = f(x) в точке х0.
Нормалью к кривой в точке с абсциссой х0 называется прямая, проходящая через эту точку перпендикулярно касательной к кривой в точке х0.
Тогда x – x0 + f ′(x0)(y – f(x0)) = 0 – уравнение нормали к графику функции y = f(x) в точке х0.
Основные правила нахождения производных
Пусть с = const, v = v(x) и u = u(x) – некоторые функции, диффе- ренцируемые в точке x0.
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. (c)′ = 0; |
|
4. (u – v)′ = u′ – v′; |
7. (u v)′ = u′ v + u v′; |
|
||||||||||||||
2. (x)′ = 1; |
|
5. (c u)′ = c u′; |
|
u ′ |
u′v − uv′ |
|
|
|||||||||||
|
8. |
|
|
|
|
= |
|
|
|
,v |
≠ 0; |
|||||||
|
v |
|
v2 |
|||||||||||||||
|
|
u ′ |
u′ |
|
c ′ |
|
cv′ |
|
|
|
||||||||
3. (u + v)′ |
= u′ + v′; 6. |
|
= |
|
; |
9. |
|
|
= − |
|
,v ≠ 0. |
|
||||||
c |
c |
v |
v2 |
|
||||||||||||||
|
Таблица производных основных функций |
|
|
|
||||||||||||||
1. (ха)′ = a xa–1; |
|
|
4. (sin x)′ = cos x; |
|
|
|
||||||||||||
2. (ax)′ = ax ln a, a > 0, a ≠ 1; (ex)′ = ex; |
5. (cos x)′ = –sin x; |
|
|
|||||||||||||||
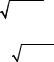
3. ( x)′ = |
1 |
; |
|
|
6. (tg x)′ = |
|
1 |
; |
|
|
||||||||
|
|
|
cos2 x |
|
|
|||||||||||||
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
||||||
93
7. |
(ctg x)′ = − |
|
1 |
|
|
; |
|
|
|
|
|
12. |
(loga x)′ = |
|
|
1 |
|
; |
(ln x)′ = |
1 |
; |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
sin 2 x |
|
|
|
|
|
|
|
|
x ln a |
|
x |
||||||||||||
8. |
(arcsin x)′ = |
1 |
|
|
; |
|
|
|
13. (sh x)′ = ch x; |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
1− x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
9. |
(arccos x)′ = − |
|
|
1 |
|
|
|
; |
14. (ch x)′ = sh x; |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1− x2 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
10. (arctg x)′ = |
|
1 |
|
|
; |
|
|
|
|
15. |
(th x)′ = |
1 |
|
; |
|
|
|
|
|
||||||
1+ x2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
ch2 x |
|
|
|
||||||||||||
11. (arcctg x)′ = − |
|
1 |
|
|
; |
16. |
(cth x)′ = − |
|
1 |
. |
|
|
|
||||||||||||
|
+ x2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
sh2 x |
|
|
|
||||||||||||
Правило дифференцирования сложной функции
Если функции y = f(x) и z = g(y) дифференцируемы соответственно в точках x0 и y0, где y0 = f(x0), то сложная функция z = g(f(x)) диффе- ренцируема в точке x0, причем z′(x0) = g ′ (y0) f ′ (x0).
Производная обратной функции
Если функция у = f(x) непрерывна и строго монотонна в некото- рой δ-окрестности Uδ(x0) точки x0 и имеет в точке x0 производную f '(x0) ≠ 0, тогда обратная к ней функция x = g(y) дифференцируема в
точке у0 = f(x0), причем g′( y0 ) = |
1 |
. |
|
||
|
f ′(x0 ) |
|
Правая и левая производная
Правой производной функции f(x) в точке x0 называется величина
f ′(x ) = lim |
f (x0 + x) − f (x0 ) |
, |
||
|
||||
+ |
0 |
x→0+0 |
x |
|
|
|
|||
если указанный предел существует.
Левой производной функции f(x) в точке x0 называется величина
f ′(x ) = lim |
f (x0 + x) − f (x0 ) |
, |
||
|
||||
− |
0 |
x→0−0 |
x |
|
|
|
|||
если указанный предел существует.
Для существования производной f ′(x0) в точке x0 необходимо и доста- точно, чтобы в этой точке функция f(x) имела правую и левую производ-
ные, и эти производные были равны между собой: f ′(x |
) = f ′(x |
) = f ′(x ). |
||
+ |
0 |
− |
0 |
0 |
94

Логарифмическая производная
Если функция y = f(x) дифференцируема в точке x0 и f(x0) ≠ 0, то логарифмической производной называется величина
′ |
f ′(x0 ) |
||
(ln f (x )) |
= |
|
. |
|
|||
0 |
|
f (x0 ) |
|
|
|
||
Функция вида y = (u(x))v(x) (u(x) > 0), где и основание и показатель изменяются вместе с независимой переменной x, называется показа- тельно-степенной. Простейшим примером такой функции является функция y = xx, x > 0.
Для дифференцирования показательно-степенной функции y = (u(x))v(x) можно применить формулу
y′ = y(ln y)′.
Например, найдем производную от функции y = xx:
y′ = xx (ln xx )′ = xx (x ln x)′ = xx (ln x + x 1) = xx (ln x + 1). x
Найти производную функции y = (u(x))v(x) можно также с помо- щью следующих свойств логарифмической функции:
a = eln a ; ln ak = k ln a.
Тогда
y = (u(x))v( x) = eln(u( x))v( x) = ev( x)ln u( x) ;
y′ = ((u(x))v( x) )′ = (ev( x)ln u( x) )′ = ev( x)ln u( x) (v(x)ln u(x))′ = = ev( x)ln u( x) (v′(x)ln u(x) + v(x)(ln u(x))′).
Для функции y = xx
y = xx = еln xx = exln x .
Тогда
y′ = exln x (x ln x)′ = xx (ln x + x 1) = xx (ln x + 1). x
95
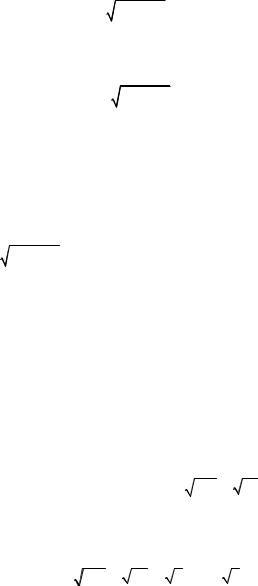
Формулу y ′ = y(lny)′ можно использовать для дифференцирования некоторых сложных функций. Например, для нахождения производ- ной от произведения
y = 5x (x2 + 1)3 tg2 x(x + 4)5
удобно применить логарифмическую производную, что позволит быстрее найти результат. Тогда
у′ = y (ln (5x (x2 + 1)3 tg7 x(x + 4)5 ))′ =
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|||
= y x ln 5 |
+ + |
ln(x2 + 1) + 7ln tg x + 5ln(x + 4) |
||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
3 2x |
|
|
7 |
|
|
|
|
5 |
|
|
|
|
|||
= y ln 5 |
+ |
|
+ |
|
|
+ |
|
|
= |
|
||||||||||
|
|
tg x cos2 |
|
|
|
x + 4 |
||||||||||||||
|
|
|
|
|
2(x2 +1) |
x |
|
|
|
|
||||||||||
= 5x (x2 + 1)3 tg2 |
x(x + 4)5 |
|
|
3x |
|
|
|
7 |
|
|
|
|||||||||
ln 5 + |
|
+ |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
x2 + 1 |
tg x cos2 x |
||||||||||
=
+ |
5 |
|
|
. |
|||
x + 4 |
|||
|
|
Пример 2.1.1
Найти производную функции y = –x4 + x3 + 2х2 + 3x + 2 в точке x0 = –1.
Решение
y' = (–x4)' + (x3)' + 2(х2)' + 3(x)' + (2)' = –4x3 + 3x2 + 4х + 3.
Тогда
y'(–1) = –4(–1)3 + 3(–1)2 + 4(–1) + 3 = 4 + 3 – 4 + 3 = 6.
Пример 2.1.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найти производную функции y = |
1 |
|
|
− |
|
2 |
|
|
в точке x0 = 2. |
||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
4 2x3 |
|
3 4x |
||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Преобразуем функцию: |
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
2 |
|
1 |
|
− |
3 |
|
2 |
− |
1 |
|
||||
y = |
− |
= |
|
x 4 − |
x 3 . |
||||||||||||
|
|
|
3 4 |
||||||||||||||
|
4 2x3 |
|
3 4x 4 2 |
|
|
|
|
|
|
|
|
||||||
96
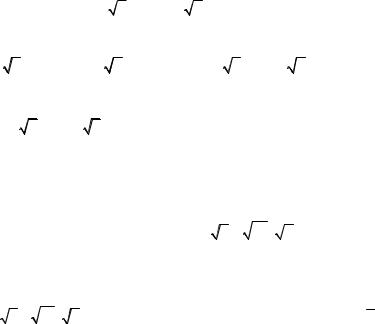
Тогда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
′ |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y′ = |
|
x− |
4 − |
|
|
|
|
x |
− 3 = |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
3 |
− |
3 |
−1 |
|
|
|
2 |
|
|
|
1 |
|
− |
1 |
−1 |
|
|
|
|
|
|
3 |
|
|
|
|
− |
7 |
|
2 |
|
− |
4 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
− |
|
x |
4 |
|
− |
|
|
|
|
|
|
− |
|
|
x |
3 |
|
|
|
|
= − |
|
|
|
|
|
|
|
x |
|
4 + |
|
|
|
x 3 . |
||||||||||||||||||||||
4 2 |
|
|
|
3 4 |
3 |
|
|
|
|
44 2 |
|
|
33 4 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
3 |
|
7 |
|
|
|
2 |
|
|
2− |
4 |
|
|
|
|
|
3 |
|
|
|
|
7 |
|
|
1 |
|
|
|
|
2 |
2− |
4 |
|
− |
2 |
|
|
3 |
|
|
|
|
2 |
|
|||||||||||||||
y′(2) = − |
|
|
2− |
|
+ |
|
|
|
|
= − |
2− |
|
− |
|
|
+ |
|
|
|
|
= − |
2−2 + |
2−2 = |
||||||||||||||||||||||||||||||||||||||
|
|
4 |
|
|
3 |
|
4 |
4 |
3 |
|
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
3 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
44 2 |
|
|
|
|
|
33 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
3 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
= − |
|
|
+ |
|
= |
|
|
− |
|
|
= − |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 4 |
3 4 |
6 |
|
16 |
48 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Пример 2.1.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 )3 x |
|
|
|
|
|
|
||||||||||||||
Найти производную функции y = 2(− 6 x + |
|
|
в точке x0 = 1. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение
Преобразуем функцию:
|
( |
|
|
) |
|
|
|
|
|
1 |
|
|
3 |
|
1 |
|
|
|
|
|
1 |
|
1 |
|
|
|
3 |
|
1 |
|
|
|
1 |
|||||||
y = 2 |
−6 |
x + x3 |
3 |
x = 2 |
−x6 + x2 x3 |
= 2 |
−x6 |
+ 3 + x2 |
+ 3 |
= 2 |
−x2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
11 |
′ |
|
|
|
|
|
|
1 |
|
1 |
−1 |
|
11 |
|
11 |
−1 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
y′ = 2 |
− x2 + x 6 |
= 2 |
− |
|
|
x2 |
|
+ |
|
|
|
|
x 6 |
|
= |
|
|
|
|||||||||||||||||||
|
|
|
|
2 |
|
|
|
6 |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− |
1 |
|
11 |
|
5 |
|
|
11 |
5 |
− |
1 |
|
||||||
|
|
|
|
|
|
|
|||||||||||||||
= 2 |
− |
|
x 2 + |
|
|
|
x6 |
= |
|
|
|
|
x6 − x 2 ; |
||||||||
2 |
6 |
|
3 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′(1) = |
11 |
− 1 = |
8 |
. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|||
11
+ x 6 .
Пример 2.1.4
Найти производную функции |
y = |
8 |
|
в точке x0 = 0. |
2x3 + 3x2 − x − 1 |
||||
97
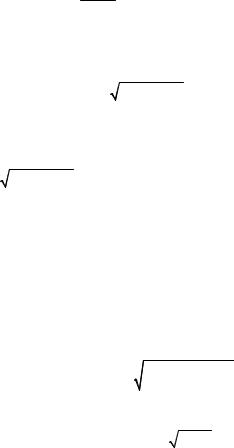
Решение
y′ = − |
8(2x3 + 3x2 − x − 1)′ |
8(6x2 + 6x − 1) |
||
|
= − |
|
; |
|
(2x3 + 3x2 − x − 1)2 |
(2x3 + 3x2 − x − 1)2 |
|||
y′(0) = − 8(−1) = 8.
(−1)2
Пример 2.1.5
Найти производную функции y = |
|
1 |
|
|
|
. |
|||
|
|
|
|
|
|||||
|
|
|
3 2x + 3 − x2 |
||||||
Решение |
|
|
|
|
|
|
|
|
|
Преобразуем функцию: |
|
|
|
|
|
|
|
||
|
1 |
= (− x2 |
+ 2x + 3) |
− |
1 |
|
|||
y = |
|
||||||||
|
3 . |
||||||||
3 2x + 3 − x2 |
|||||||||
|
|
|
|
|
|
|
|
||
Воспользуемся правилом нахождения производной сложной функции
(f(g(x))′ = f ′(g(x))g′(x).
Тогда
|
|
|
|
1 |
|
|
|
|
|
|
|
) |
− |
1 |
−1 |
(− |
|
|
|
|
|
′ |
|
|
|
|
|
|
= − |
|
|
+ |
|
|
+ |
|
|
|
+ |
|
+ |
|
= |
|
|
||||||
|
|
y′ |
3 (− |
x2 |
2x |
3 |
3 |
|
x2 |
2x |
3 |
) |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= − 1 (− x2 + 2x + 3)− 3 (−2x |
+ 2) = |
|
|
2x − 2 |
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33 (− x2 + 2x + 3)4 |
||||||||||
Пример 2.1.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найти производную функции y = (2 − x)2 + |
1− x2 |
. |
|||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
Решение
Воспользуемся правилом нахождения производной сложной функции:
(f(g(x))′ = f ′(g(x))g′(x).
98

Тогда |
|
|
|
|
|
|
|
|
|
|
|
y′ = ((2 − x)2 )′ + |
1 |
( 1− x2 |
)′ = 2(2 − x)(2 − x)′ + |
1 |
1 |
|
(1− x2 )′ = |
||||
|
|
|
2 1− x2 |
||||||||
2 |
|
|
|
2 |
|
|
|||||
= 2(2 − x)(−1) + |
|
−2x |
= −2(2 − x) − |
|
|
x |
. |
|
|||
|
1− x2 |
|
|
|
|
||||||
|
|
4 |
2 |
|
1− x2 |
|
|||||
Пример 2.1.7
Найти производную функции y = 6xsin x.
Решение
Воспользуемся правилом нахождения производной произведения двух функций
(uv)′ = u′v + uv′.
Тогда
y' = (6x)′sin x + 6x(sin x)' = 6xln6 sin x + 6xcos x.
Пример 2.1.8
Найти производную функции y = |
1 |
− log |
|
(2x − 3) . |
|||
sin(2x) |
2 |
||||||
|
|
|
|
|
|
||
Решение |
|
|
|
|
|
||
Преобразуем функцию: |
|
|
|
|
|||
y = |
1 |
− log2 (2x − 3) = (sin (2x))−1 − log2 (2x − 3). |
|||||
sin (2x) |
|||||||
|
|
|
|
|
|
||
По правилу нахождения производной сложной функции y′ = ((sin (2x))−1 )′ − (log2 (2x − 3))′ =
= − (sin (2x))−2 (sin (2x))′ − |
|
1 |
|
|
|
|
(2x − 3)′ = |
||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
(2x − 3)ln 2 |
( |
|
) |
|
|
|
||||||
= − (sin (2x)) |
− |
2 |
(cos(2x))(2x)′ − |
|
2 |
|
|
|
2cos |
2x |
2 |
|
|||||
|
|
|
|
|
= − |
|
|
− |
|
. |
|||||||
|
|
|
|
|
|
|
|||||||||||
|
|
(2x − 3)ln 2 |
sin2 (2x) |
(2x − 3)ln 2 |
|||||||||||||
Пример 2.1.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Найти производную функции y = |
x + 2 − 1 |
. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
99
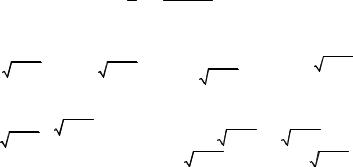
Решение
Воспользуемся правилом нахождения производной частного
u ′v
Тогда
=u′v − uv′ .
v2
y′ = ( x + 2 − 1)′ x − ( |
x + 2 − 1)x′ = 2 x + 2 (x + 2)′ x − ( |
x + 2 − 1) = |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
x |
− x + 2 |
+ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x − 2(x + 2) + 2 x + 2 |
|
|
2 x + 2 |
− x − 4 |
|
|
||||||||||
|
2 x + 2 |
|
|
|
|
||||||||||||||
= |
|
|
|
= |
= |
. |
|||||||||||||
|
x2 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2x2 x + 2 |
2x2 x + 2 |
||||||||||||
Пример 2.1.10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
Найти производную функции |
y = − |
|
. |
|
|
|
|||||||||||||
(1+ cos x)3 |
|
|
|
||||||||||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Преобразуем функцию: |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
y = − |
|
2 |
|
= −2(1+ cos x)−3 . |
|
|
|
|
||||||||
|
|
|
|
(1+ cos x)3 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
По правилу нахождения производной сложной функции
y′ = −2(−3)(1+ cos x)−3−1 (1+ cos x)′ = |
|
|||
= 6(1+ cos x)−4 (0 + (− sin x)) = − |
|
6sin x |
. |
|
(1 |
+ cos x)4 |
|||
|
|
|||
Пример 2.1.11
Найти производную функции y = log52 (2 − x) .
Решение
По правилу нахождения производной сложной функции
y′ = 5log24 (2 − x)(log2 (2 − x))′ = 5log24 (2 − x) |
|
1 |
|
(2 |
− x)′ = |
||||
|
− x)ln 2 |
||||||||
|
|
|
(2 |
|
|
||||
= 5log24 (2 − x) |
|
1 |
(−1) = − |
5log24 (2 − x) |
. |
|
|||
|
− x)ln 2 |
|
|
||||||
(2 |
|
(2 − x)ln 2 |
|
|
|||||
100
