
Закон Ампера
Ампер, исследуя влияние магнитного поля на проводник с током, установил, что сила, действующая на элемент тока равна
![]() ,
(1)
,
(1)
где
![]() элемент проводника с током
элемент проводника с током![]() .
Направление вектора
.
Направление вектора![]() совпадает с направлением тока.
совпадает с направлением тока.![]() - индукция МП. Направление силы находится
согласно правилу левой руки или согласно
определению векторного произведения.
Модуль силы определяется
- индукция МП. Направление силы находится
согласно правилу левой руки или согласно
определению векторного произведения.
Модуль силы определяется
![]() ,
(2)
,
(2)
угол
![]() между векторами
между векторами![]() и
и![]() .
.
Мы знаем, что ток создает магнитное
поле, а также, что внешнее магнитное
поле оказывает влияние на ток, поэтому
интересно рассмотреть два параллельных
прямых проводника, по которым текут
токи
![]() и
и![]() .
Каждый из токов создает свое магнитное
поле, которое воздействует на другой
ток. Сила такое действия – это сила
Ампера.
.
Каждый из токов создает свое магнитное
поле, которое воздействует на другой
ток. Сила такое действия – это сила
Ампера.

Пусть первый ток создает поле
![]() .
В этом поле на второй ток действует сила
Ампера
.
В этом поле на второй ток действует сила
Ампера![]() .
Т.к. угол между током
.
Т.к. угол между током![]() и полем
и полем![]() прямой, то величина силы Ампера равна
прямой, то величина силы Ампера равна
![]()
Величина магнитного поля, создаваемого
прямым током
![]() равна
равна ,
где
,
где![]() - расстояние между токами (эту формулу
получим в дальнейшем). Тогда сила,
действующая на второй ток, определяется
токами
- расстояние между токами (эту формулу
получим в дальнейшем). Тогда сила,
действующая на второй ток, определяется
токами

Аналогично можно найти выражение для силы, действующей на первый ток со стороны второго тока.
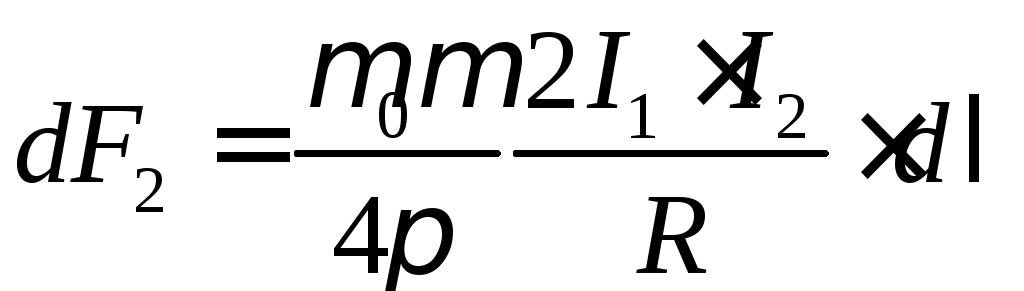
Замечаем, что силы по величине равны, но направлены в противоположные стороны.
![]()
Величина силы взаимодействия двух токов
 .
.
Два одинаково направленных тока притягиваются друг к другу. Токи, напрвленные в противоположные стороны, отталкиваются.
Сила лоренца
Т.к. ток - это направленное движение
зарядов, то на движущийся заряд со
стороны внешнего магнитного поля
действует сила. Лоренц получил формулу
для силы, которая действует на движущийся
точечный заряд
![]() со стороны магнитного поля
со стороны магнитного поля![]() .
.
![]() (1)
(1)
![]() - скорость заряда. Направление силы
Лоренца для
- скорость заряда. Направление силы
Лоренца для![]() определяется согласно правилу левой
руки, либо согласно векторному
произведению. Модуль силы Лоренца равен
определяется согласно правилу левой
руки, либо согласно векторному
произведению. Модуль силы Лоренца равен
![]()
Для
![]() сила равна нулю. Когда угол равен
сила равна нулю. Когда угол равен![]() ,
сила имеет величину
,
сила имеет величину![]() .
Т.о. сила Лоренца изменяет скорость
только по направлению. Следовательно,
магнитное поле не совершает работы над
движущейся заряженной частицей. Когда,
кроме магнитного поля, есть электрическое
поле, полная сила Лоренца
.
Т.о. сила Лоренца изменяет скорость
только по направлению. Следовательно,
магнитное поле не совершает работы над
движущейся заряженной частицей. Когда,
кроме магнитного поля, есть электрическое
поле, полная сила Лоренца
имеет вид
![]() .
(2)
.
(2)
Рассмотрим движение точечной заряженной
частицы в однородном магнитном поле.
Пусть
![]() .
В этом случае величина силы Лоренца
равна
.
В этом случае величина силы Лоренца
равна![]() .
В этом случае частица всегда остается
в плоскости, перпендикулярной магнитному
полю. Поскольку по величине скорость
не изменяется, то траекторией движения
является окружность. Поскольку частица
двигается по окружности на неё, кроме
силы Лоренца действует центростремительная
сила. Для любой точки траектории
выполняется равенство сил.
.
В этом случае частица всегда остается
в плоскости, перпендикулярной магнитному
полю. Поскольку по величине скорость
не изменяется, то траекторией движения
является окружность. Поскольку частица
двигается по окружности на неё, кроме
силы Лоренца действует центростремительная
сила. Для любой точки траектории
выполняется равенство сил.
 .
Отсюда находим радиус окружности
.
Отсюда находим радиус окружности .
Период вращения
.
Период вращения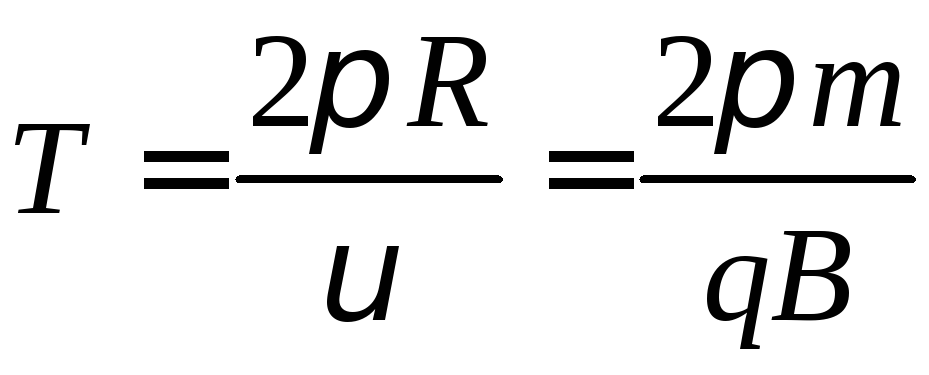 .
Для нерелятивистской частицы период
не зависит от скорости. Поведение частицы
в МП лежит в основе конструкции
ускорителей. Для произвольной ориентации
скорости частицы и направления магнитного
поля, скорость можно разложить на
параллельную и перпендикулярную
компоненты:
.
Для нерелятивистской частицы период
не зависит от скорости. Поведение частицы
в МП лежит в основе конструкции
ускорителей. Для произвольной ориентации
скорости частицы и направления магнитного
поля, скорость можно разложить на
параллельную и перпендикулярную
компоненты:![]() .
В этом случае радиус окружности
определяется
.
В этом случае радиус окружности
определяется![]() :
: .
За период
.
За период![]() частица пройдет расстояние вдоль поля
равное
частица пройдет расстояние вдоль поля
равное![]() .
Если сложить эти два движения, то получим
траекторию, которая является винтовой
линией или спиралью с шагом
.
Если сложить эти два движения, то получим
траекторию, которая является винтовой
линией или спиралью с шагом

где
![]() - угол между скоростью и магнитным полем.
Пусть магнитное поле неоднородное,
угол
- угол между скоростью и магнитным полем.
Пусть магнитное поле неоднородное,
угол и поле
и поле![]() растет в направлении
растет в направлении![]() ,
тогда
,
тогда![]() и
и![]() уменьшаются с ростом
уменьшаются с ростом![]() .
На этом эффекте основана фокусировка
заряженных частиц в магнитном поле.
.
На этом эффекте основана фокусировка
заряженных частиц в магнитном поле.
