Колебания

Гармонические колебания.

Колебания – это периодические процессы. Они имеют различную природу. Для гармонических колебаний изменяющаяся во времени величина подчиняется закону косинуса (синуса). Гармонические колебания описываются уравнением вида:

(1)

- значение изменяющейся во времени величины. - амплитуда, - циклическая частота, - начальная фаза. Величина называется фазой колебания. Время, когда система возвращается в исходное состояние, называется периодом. Обозначается - . Фаза колебания зависит от времени и через период она примет вид

Поскольку система через период возвращается в исходное состояние, поэтому должно выполняться условие

или (2)

Величина называется частотой. Связь циклической частоты и частоты :

(3)

Единица измерения частоты – герц (1 Гц). Если продифференцировать дважды по времени уравнение (1), получим дифференциальное уравнение гармоноческих колебаний:

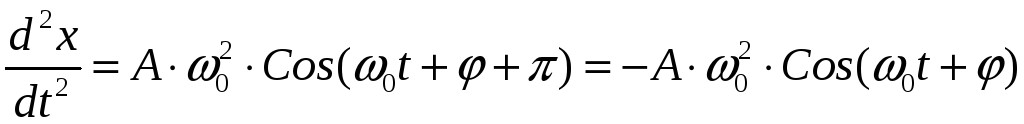или (4 )

(4)

Гармонические колебания хорошо изображаются методом вращения вектора амплитуды. Закон движения можно записать, используя комплексное представление

(5)

В зависимости от внешнего воздействия на систему колебания могут быть: свободными, вынужденными, автоколебаниями и параметрическими. Свободные колебания – колебания системы без внешних воздействий. Вынужденные колебания – на систему постоянно действует внешняя периодическая сила. Автоколебания – это вынужденные колебания, когда действие внешней силы задается самой системой (работа сердца). Параметрические колебания – колебания, в которых происходит изменение параметра системы за счет внешних сил. Рассмотрим механические колебания.

Математический маятник.

Точечная масса подвешена на невесомой нерастяжимой нити длиной . Система находится в поле тяжести. Выберем систему координат. Ось направим вдоль ускорения свободного падения. Колебания массы происходит в плоскости .

Длина маятника . Масса -. Внешняя сила – сила тяжести. Координаты векторов , , .

Движение массы происходит по окружности. Уравнение движения в этом случае имеет вид

, (1)

где - момент импульса, - импульс, - момент силы.

Проекции маятника на оси и равны: , . Момент силы направлен вдоль оси . Тогда имеем соотношение

, , или

Последнее соотношение получили из представления векторного произведения в виде определителя, после чего раскрыли определитель по первой строке и взяли только - компоненту. Матрица, определитель которой раскрывали, имеет вид:

Аналогично для момента импульса. Вектор момента импульса направлен вдоль оси . Следовательно, у него всего одна - компонента.

, .

Матрица определителя имеет вид

Выражение для распишем:

или .

Уравнение движения (1) имеет только одну - компоненту:

или (2)

Подставляя значение компонент в ур. (2), получаем

Дифференцируем, проводим алгебраические преобразования, получаем:

Когда угол отклонения мал, имеем . Уравнение движения примет вид:

(8)

Это уравнение математического маятника. Частота колебаний маятника равна

(9)