с.м.чернов_квантовая механика

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Могилёвский государственный университет им. А. А. Кулешова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

= a1α + a2β.

Построим теперь операторы спина электрона Q^ , которые определим в

соответствии с общим правилом:

f (ms )= Q^ϕ(ms ).

.pdf

Скачиваний:

Добавлен:

22.03.2016

Размер:

2.6 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 209 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

вым магнитным моментом μs S . В этой системе координат ядро движется,

образуя электрический ток, и по закону Био-Савара-Лапласа создает магнитное поле B ~ L . Магнитное поле ядра действует на спиновой магнитный момент электрона, потенциальная энергия которого равна:

Uсо = −μs B S L .

(33.7)

Выберем ось Z вдоль вектора L , тогда Uco Sz L = ± h2 L . Отсюда следует, что

все s -уровни (l = 0) остаются одиночными, т.к. Uco = 0 . Если же l ≠ 0 , то к энергии Enl , определяемые кулоновскими силами, либо добавляется, либо

вычитается энергия СО-взаимодействия. Следовательно, эти уровни расщепляются на две компоненты, в зависимости от ориентации спина относительно орбитального момента.

Замечание 1. Наличие собственного механического момента (спина) является атрибутом не только электронов. Приведем некоторые примеры

s = 0		π, K − мезоны;
s =	1	e± , p,n,ν,Λ0 − гиперон;
	2
s =1		γ, ρ − мезоны;
s =	3	Ω− − гиперон;
	2
s = 2		G − гравитон, А2 − мезон.

Важно отметить, что в природе существуют лишь

Sдва сорта микрочастиц: с целым спином (бозоны), или с полуцелым спином (фермионы). Практически окружающий нас мир (атомы, атомные ядра) построен из фермионов.

Замечание 2. Покажем, что наличие спина нельзя интерпретировать классически как вращение электрона вокруг своей оси. В настоящее время экспериментально до-

казано, что размеры электрона r0 ≤10−17 м. Для простоты будем считать, что

вся масса электрона сосредоточена по экватору. Тогда вращательный момент электрона (спин) будет равен:

S = m r v = h 3			h.
0	0	4
		4

Следовательно, линейная скорость вращения электрона будет иметь порядок:

v =	S				10−34			13	м
			≥					=10		.
	m r		≥	10		−30	−17	=10	с	.
	m r			10		10			с
	0	0
						81

Эта оценка на 5 порядков превышает скорость света с = 3 108 мс , что физически не допустимо.

§ 34. Полуэмпирическая теория спина электрона

Как уже отмечалось, наличие спина электрона можно строго обосновать в рамках релятивистской квантовой механики Дирака. Однако ряд свойств частиц со спином может быть описано и без привлечения строгой теории, а на основании общих квантовомеханических соображений и небольшого числа экспериментальных фактов.

Волновая функция частицы со спином зависит не только от пространственных координат и времени, но и спиновых переменных. Величина спина

определяется двумя квантовыми числами	s =	1	,ms	= ±	1	, которые опреде-
		2			2

ляют модуль вектора спина и его проекции на ось Z . Поэтому, в качестве спиновой переменной выберем дискретную величину ms . Если пространст-

венные и спиновые переменные являются независимыми (что возможно при пренебрежении спин-орбитальным взаимодействием), то волновую функцию можно представить в виде произведения:

ψ (r,t,ms ) =ψ (r,t )ϕ(ms ). (34.1)

При этом спиновая часть волновой функции, фактически, может принимать лишь два, вообще говоря, комплексных значения:

	+	1	≡ a1;		−	1	≡ a2 ,	(34.2)
ϕ	+	2	≡ a1;	ϕ	−	2	≡ a2 ,	(34.2)
		2				2

которые удобно представить в виде матрицы-столбца:

ϕ(m )=

(34.3)

Физический смысл параметров

состоит в том, что

есть вероят-

Sz =

ности того, что проекции спина

имеют

значения,

соответственно:

иSz = −h2 , при этом должно выполняться условие нормировки:

a	2	+	a	2	2	=1.	(34.4)

1

Таким образом, любая спиновая функция электрона представляет собой столбец из двух комплексных чисел (34.3), связанные условием нормировки

(34.4).

Особый смысл имеют волновые функции вида:

	1	;		0		(34.5)
α =	0	;	β =	1	.	(34.5)
	0			1

Очевидно, функция α описывает спиновое состояние электрона с проекцией

Sz	=	h	, а β	– соответствует S		= −	h	. Действительно, в первом случае
	2				z	2

a1 =1, a2 = 0, и, следовательно, вероятность обнаружения положительной проекции спина a1 2 =1.

Важность этих функций состоит в том, что они образуют базис в про-

странстве спиновых переменных, т.к. любую спиновую функцию всегда мож-

но представить в виде линейной комбинации этих функций:

Так как спиновые функции представляют собой матрицу-столбец, то общий вид спиновых операторов следует искать в виде:

Q^	q	q		(34.6)
Q^	= 11	12	.	(34.6)
	q21	q22

Чтобы найти явный вид спиновых матриц, учтем 3 основных обстоятельства:

1) Из опыта известно, что величина спина и его проекции равны:
				S2 = h2s(s +1)= 3 h2 ;							S			= hm = ±				h	.	(34.7)
				S2 = h2s(s +1)= 3 h2 ;							S	z		= hm = ±					.	(34.7)
									4			z			s		2
									4								2
2) Спиновые операторы, как и операторы орбитального момента, удов-
летворяют коммутационным соотношениям вида:
	$	$			$		$	$		$				$	$		$			(34.8)
S x ,S y				= ihS z ;		S z , S x			= ihS y ;		S y ,S z					= ihS x ;				(34.8)

			$2	$				$2	$	= 0;			$2		$		= 0;			(34.9)
		S		,S x	= 0;		S		, S y	= 0;			S		,S z		= 0;			(34.9)

3) Если матрицу привести к диагональному виду, то диагональные матричные элементы равны собственным значениям соответствующего оператора.

На основании этих утверждений, в Z -представлении сразу можно запи-

$	:
сать явный вид оператора S z	:
		h		0
								1	0
$			2				h	1	0
S z		=				=		0	.	(34.10)
S z		=				=	2		.	(34.10)
			0	−	h		2		−1

					2
					2

В дальнейшем удобно выделить множитель h2 , т.е. представим:

$	h $
S =		σ.	(34.11)
	2
Двухрядные матрицы σ x ,σ y ,σ z называются матрицами Паули.			Вид всех

матриц Паули можно найти из соотношений (34.8) с учетом (34.10), которые можно также привести к виду:


σ x ,σ y	= 2iσ z ; σ z ,σ x	= 2iσ y ;

Приведем здесь окончательный результат:

	0		1	;		0 −i		;
σ x =		1	0		σ y =		0
						i

σ y ,σ z = 2iσ x .

	1	0
σ z =	0	.
	0	−1

(34.12)

(34.13)

Отметим некоторые свойства матриц Паули. Найдем произведение матриц

σ x и σ y :

		0	1 0 −i			i		0	1 0
σ x σ y =		1			0	=	0	−i	= i	0			= iσ z ;
			0 i									−1			(34.14)
		0	−i 0		1	−i		0			1	0

σ y σ x =				1	0	=	0 i		= −i		0			= −iσ z .
	i		0									−1

Аналогичные формулы получаются и для других пар матриц. Вычитая из первого равенства второе, мы убеждаемся в справедливости условий (34.12). Складывая же эти у равнения, получим свойство антикоммутативности матриц Паули:

σ x σ y +σ y σ x =σ x σ z +σ z σ x =σ y σ z +σ z σ y = 0 .

(34.15)

Легко убедится, что квадраты матриц Паули равны единичной матрице:

					2			2		2		$			1 0
					σ x =			σ y =σ z				= I	=		0	1	.
															0	1
2		0 1				0 1					1 0				Тогда, для оператора
Например: σ x	=σ x σ x =		1 0				1 0			=			.		Тогда, для оператора
			1 0				1 0				0 1
чим ожидаемый результат:													3		2	1	0
			$	2		$	2	$	2	$		2	3		2	1	0
			$			$		$		$				h				.
			S		= S x			+ S y + S z =					4	h		0	1	.
													4			0	1

(34.16)

S полу-

(34.17)

$2	$
Важно подчеркнуть, что матрицы S	и S z можно одновременно при-
	$	и
вести к диагональному виду в Z -представлении, в отличие от матриц S x		и
$
S y , что непосредственно следует из соотношений (34.8).
84

ГЛАВА IV

Приближенные методы квантовой механики

§ 35. Квазиклассическое приближение.

Метод Вентцеля-Крамерса-Бриллюэна (ВКБ-приближение)

Для простоты рассмотрим одномерное движение микрочастицы в стационарном поле U (x). Динамика ее движения описывается стационарным

уравнением Шрёдингера (УШ):

−	h2	d 2ψ (x)	+U (x)ψ (x)= Eψ (x)	(35.1)
	2m	dx2

Подобно тому, как любое комплексное число можно представить в виде z = ρ eiα , запишем решение УШ в виде:

S(x)

ψ (x)= eh

(35.2)

Подставляя (35.2) в (35.1), имеем:

dψ

S(x) dS

d 2ψ

S(x) i d 2S (x)

dS (x)

= eh

−

Отсюда, сокращая на e

S(x) , получаем уравнение для функцииS (x):

d 2 S

(x)

dS (x) 2

−

+ 2m(E −U (x))= 0 .

(35.3)

Вообще говоря, функция S = S (x, h)

может зависеть от h как от пара-

метра. Будем искать решение

уравнения (35.3) приближено, представив

S = S (x, h) в виде разложения по степеням h:

S (x, h) = S0 (x)+ hS1 (x)+ h2 S2 (x)+...,

(35.4)

где Si (x) уже не зависят от h. Причем, для дальнейшего ограничимся лишь членами не выше линейной степени h:

S (x) ≈ S0 (x)+ hS1 (x).

(34.5)

Подставляя (35.5) в уравнение (35.3), получаем:

d 2S

+ h

(E −U (x))= 0

20 + h

−

+ 2m

Последнее равенство имеет место тождественно, если равны нулю ко-

эффициенты, стоящие при одинаковых степенях h:

2m(E −U (x))

(35.6)

i	d 2S		−	dS		dS	= 0.
i		0	−		0	1	= 0.
	dx2			dx		dx

Решение уравнения (35.6) можно выразить через импульс p(x)= 2m(E −U (x)):

dS0

= ±p

(x);

S0 = ± ∫ pdx.

Отсюда, для S1 (x) получаем:

dS1

dS0

: dS0

ln dS0

ln p;

2 dx

S =

ln p = i ln

Таким образом, с точностью до линейных по h членов, имеем:

S (x)= S0 (x)+ hS1 (x)= ± ∫x	pdx +ihln p.
x0

Следовательно, приближенная волновая функция примет вид:

	i		x					x
ψ (x)= ehS (x)		= exp	± ∫ pdx − ln	p	=	1	exp	± ∫	pdx .
ψ (x)= ehS (x)		= exp	± ∫ pdx − ln	p	=	p	exp	± ∫	pdx .
			xo			p		xo
			xo					xo

(35.7)

частицы

(35.8)

(35.9)

(35.10)

Вообще говоря, решения со знаком (+) или (–) являются линейно независимыми, тогда общее решение будет представлять собой линейную комбинацию полученных частных решений:

			i	x				i	x
	c			∫ pdx		c	−		∫	pdx
				∫ pdx			−		∫	pdx
			hx					h x
ψ =	1	e		o	+	2	e		o	.	(35.11)
ψ =	p	e		o	+	p	e		o	.	(35.11)
	p					p

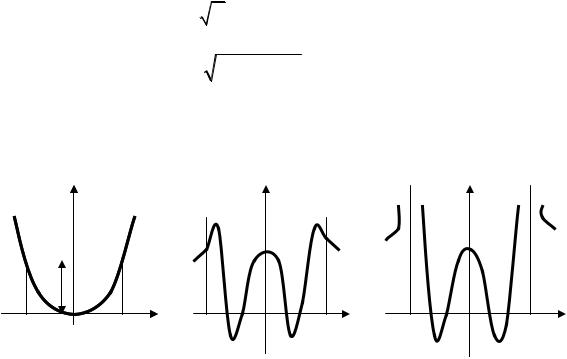
Рассмотрим случай, когда частица движется в одномерной потенциаль-

ной яме произвольной формы, но имеющей один минимум (рис. 12).

U (x)

E	II	I
E		I
		I
		I
		I	II	III
		a	b		x

Рис. 12. Движение частицы в яме с одним минимумом

Очевидно, области I и III, где U (x)≥ E являются классически недоступными. Для этих областей импульс является чисто мнимым:

p = 2m(E −U ) = i 2m(U − E ) = i

где введено обозначение

2m(U − E ) .

Следовательно, волновая функция представляет собой экспоненциально

возрастающее или убывающее решение:

ψ =

e−h∫

dx +

eh∫

dx .

(35.12)

Так как бесконечно возрастающее решение не имеет физического смысла, то решение для I и III области должны иметь следующий вид:

−

1 a

−

1 a

∫

(x ≤ a) ψ

h x

(35.13)

−

1 x

−

1 x

∫

(x ≥ b) ψ2

(35.14)

где введены обозначения c =

;

Во II области мы имеем осциллирующее решение, выраженное через комбинацию экспонент с мнимыми показателями (35.11), зависящее от параметров c1 и c2 . Необходимо сшить экспоненциальное и осциллирующее ре-

шение на границах x = a и x = b, причем так, чтобы оба они аппроксимировали одно и то же решение точного УШ.

Опуская громоздкие математические преобразования, приведем окончательный результат. Сшивая решения на правой границе ямы x =b , можно показать, что

		B	iπ			B		−i	π
c	=		e 4 ;	c	=		e		4 .
c	=		e 4 ;	c	=		e		4 .
1		2		2		2
		2				2

Тогда решение во II области (x < b) примет вид:

i x

1 x

∫

pdx

−

∫

pdx

∫

pdx+

−i

∫

pdx+

ψII =

+ e

(35.15)

1 x

cos

∫ pdx +

sin

−

∫ pdx +

h b

B		1 b	π
	sin	∫ pdx +
	sin	∫ pdx +
p	h x		4	.

При вычислениях мы воспользовались очевидными соотношениями:

eiα + e−iα = 2cosα = 2sin π						−α .
					2
Аналогично, сшивая решения на левой границе ямы (x = a), получаем
другое решение для той же области II (x > a), в виде:
%′	A		1 x	π
		sin	∫ pdx +		.	(35.16)
ψII =	p			4
		h a
В общем, полученные решения не справедливы в граничных точках при
x = a и x = b, где E =U и p =	2m(E −U ) → 0 . Для иллюстрации приведем

графики поведения волновой функции линейного гармонического осциллято-


ра U (x)=			mω2 x2	для квантового числа n = 5 (рис. 13).
ра U (x)=				для квантового числа n = 5 (рис. 13).
			2
			U(x)			ψ(x)		ψвкб(x)
		n=5

			E
	a			b x	a	b x	a	b x

Рис. 13. Зависимость волновой функции осциллятора от х для n = 5 . (точное решение УШ – ψ (x); ВКБ – приближение – ψвкб (x))

Интересно отметить, что для II области мы получим две волновые функции ψ%II и ψ%II′ (35.15) и (35.16). Так как они описывают одно и тоже состояние в

каждой точке интервала [a,b], то они должны совпадать. Это требование уста-

навливает связь между коэффициентами А и В, а также между аргументами синусов. Для дальнейшего удобно воспользоваться очевидным соотношением:

sinα = (−1)n sin (n +1)π −α ; n = 0, ±1, ±2,...,

которое легко проверяется на единичной окружности:

n = 0 sinα =sin (π −α)= sinα;

n =1 sinα =(−1)sin (2π −α)= (−1)(−1)sinα =sinα;

..........................................................................................

Тогда ψ%II′ можно представить в виде:

%′		A		1 x	π
	=		sin	∫ pdx +		=
ψII		p			4
			h a

A(−1)n		1 x	π
	sin (n +1)π −	∫ pdx −	4
p
		h a

Сравнивая последнее соотношение с волновой функцией ψ%II (35.15):

1 b

sin

∫ pdx

ψII =

h x

%′

мы видим, что равенство ψII

=ψII имеет место при выполнении условий:

(n +1)π −

B = A(−1)n

∫ pdx + π

1 ∫ pdx − π = 1

h a

h x

Учитывая, что ∫

+ ∫

= ∫

отсюда получаем:

1 b

= (n +1)π −

∫ pdx

=π n +

или

h a

∫ pdx

=πh n +

Так как p ≥ 0 и b ≥ a , то n ≥ 0 , следовательно

n = 0,1,2,...

Учитывая симметрию в движении частицы слева направо и в обратном направлении, получаем знаменитое условие квантования Бора-Зоммер-

фельда:

ο pdx = 2b		pdx = 2πh		n +	1	.		(35.17)
∫	∫				2
	a				2		1
Это соотношение отличается от			квазиклассического членом				1	в круг-
							2

лых скобках. Практически эти две формулы совпадают при больших кванто-

вых числах n.1

Найдем, наконец, приближенно нормировочный множитель А при больших n При этом будем пренебрегать экспоненциально убывающим решением вне ямы, и учтем, что при больших n аргумент синуса также является большим и квадрат синуса становится быстро осциллирующим, который с

хорошей точностью можно заменить на среднее значение, равное 12 . Тогда условие нормировки примет вид:

%′

2 b

1 x

1 = ∫

dx = A

∫

sin

∫ pdx +

p(x)

h a

A2 b dx

A2 b

A2 π

∫

∫dt =

2m 2

2m ω

a mv

2m a

π	≈	A2	b dx		=
			∫	p
4		2
			a

π A2 , 2mω

где T = 2ωπ – период движения частицы в яме. Отсюда окончательно получа-

ем:

%′

2mω

1 x

2ω

1 x

(35.18)

ψII

π p

sin

∫ pdx +

πv

sin

∫ pdx +

h a

Замечание. Условия применимости ВКБ-приближения.

Очевидно, разложение (35.4) будет давать хорошее приближение, если этот ряд быстро сходится. Для этого необходимо выполнения условия:

hS1

(35.19)

которое после дифференцирования по х, примет вид:

dS1

dS0

(35.20)

Учитывая, соотношение (35.8), имеем:

dS0

= p(x)=

2m(E −U (x)),

(35.21)

откуда, в частности:

−2m dU

= m

(35.22)

2 p

Далее, учитывая соотношение (35.9) S

(x)=

ln p(x), получим:

dS1

ln p(x)

2 p

2 p2

Тогда неравенство (35.19) примет вид:

(35.23)

Таким образом, квазиклассическое приближение справедливо для достаточно быстрых частиц, которые движутся в полях, медленно меняющихся в пространстве.

Как уже отмечалось, ВКБ-приближение не справедливо в граничных точках x = a и x = b, в которых E =U. Это связано с тем, что в точках пово-

рота импульс р = 0, а волновая функция ψII 1p → ∞ , и не удовлетворяет

стандартному условию конечности.

Полученное условие (35.23) позволяет оценить расстояние до точки поворота а, в которой E =U (a), когда еще можно пользоваться квазиклассиче-

ским приближением. Для этого разложим потенциальную энергию U (x) в ряд Тейлора в окрестности точки а:

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 209 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.04.2015501.2 Кб568решебник.docx
#
18.04.201513.95 Кб13россия.docx
#
11.07.201913.89 Mб14Рубинштейн С.Л. Основы общей психологии.rtf
#
22.08.201930.64 Кб5русский СЕЛЕЗНЁВА(ТРХ-111).docx
#
25.09.201969.55 Кб7с группы.docx
#
22.03.20162.6 Mб61с.м.чернов_квантовая механика.pdf
#
18.04.2015197.73 Кб38савицкая .docx
#
18.04.2015173.57 Кб14Сведения о родителях 2014-2015.doc
#
18.04.2015447.02 Кб13Сельский туризм.pdf
#
15.08.201956.85 Кб0сем1.docx
#
11.11.2019243.71 Кб9Семаго содер и организ.doc