
Lektsii_PDF / Лекция_8
.pdf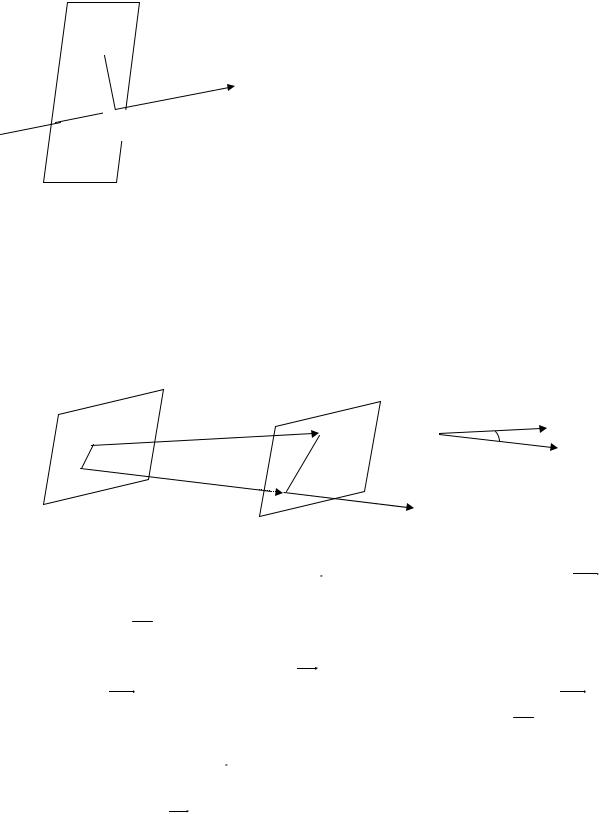
Лекция № 8
Проекция точки и вектора на ось
M
X
M '
O
P
Осью называется прямая, для которой указано направление.
Проекцией точки на ось называется основание перпендикуляра из точки M на ось OX . Плоскость P OX . Следовательно, точка M ' является проекцией точки M на ось OX .
Рассмотрим отрезок AB и ось u . Спроектируем точки A и B на ось u , то есть проведем плоскости α и β , проходящие соответственно через точки A и B ортогонально u :
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
M |
|
||
|
|
|
|
|
|
|
|
|
B |
|
|
|||
|
|
A |
|
|
|
ϕ |
||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
v |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
A |
' |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
B' |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Геометрической проекцией вектора AB на ось u называется вектор A 'B' ,
где A' есть проекция точки A , а B' есть проекция точки B на ось u . Обозначается:
Алгебраической проекцией вектора AB на ось u называется число, равное длине вектора A 'B' , взятое со знаком «+», если направление вектора A 'B' и оси u совпадает, знак «-» - в противном случае. Обозначается:
Углом наклона вектора AB к оси u называется угол ϕ , образованный двумя лучами, приложенными к точке M , один из которых совпадает с направлением вектора AB , а другой – с направлением оси u .
Теорема 8.1.
1

Алгебраическая проекция вектора a на произвольную ось u
определяется по формуле: прu |
AB |
= |
|
a |
|
cosϕ , |
где ϕ - угол наклона |
|
|
||||||
вектора a к оси u . |
|
||||||
Доказательство. Проведем через точку A ось v , |
параллельную оси u , и |
||||||
спроектируем точку B на ось v . |
|
||||||
|
|
α |
β |
M |
|
|
|
||
|
A |
|
B |
ϕ |
A |
' |
|
C |
v |
|
|
|||
|
|
|
|
|
|
|
|
B' |
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
Из построения |
следует, |
что |
AC |
= A 'B' , |
|
AC |
A 'B' |
. Из |
ABC следует: |
|||||||||||
|
|
= |
|
cosϕ , |
|
|
= пр a = |
|
cosϕ . |
|
|
|
|
|
|
|||||
|
AC |
a |
|
A 'B' |
a |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 8.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Декартовые координаты вектора d |
равны алгебраическим проекциям |
||||||||||||||||
|
|
|
вектора d на координатные оси OX ,OY ,OZ . |
|
||||||||||||||||
Доказательство. |
Поместим |
вектор d в |
начало координат. |
Через конец |
||||||||||||||||
вектора проведем плоскости, параллельные координатным плоскостям. Точки пересечения с осями координат обозначим A, B,C .
|
|
Z |
|
|
|
|
|
|
|
|
|
D |
|||
C |
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Y |
|
|
k |
|
j |
B |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
X |
|
O |
A |
|
|
|
|||
|
|
|
|
||||
i |
|
|
|
|
|||
|
|
|
|
||||
|
|
|
|
|
|
|
|
Вектор d = OD = OA + OB + OC , где OA,OB,OC - геометрические проекции на оси
OX ,OY ,OZ . Вектор OA коллинеарен орту i , OB коллинеарен орту j , OC коллинеарен орту k . Поэтому на основании теоремы о коллинеарных
векторах найдутся такие числа |
x, y, z , что будут справедливы следующие |
||||||||||||
соотношения: |
|
= xi , |
|
= yj , |
|
= zk . |
|
|
|
|
|
|
|
OA |
OB |
OC |
Поэтому окончательно |
можно |
|||||||||
записать: d = xi + yj + zk . Следовательно |
тройка чисел {x, y, z} являются |
||||||||||||
|
d . При |
|
|
|
|
|
|
равны: |
|||||
координатами вектора |
этом длины векторов OA,OB,OC |
||||||||||||
2
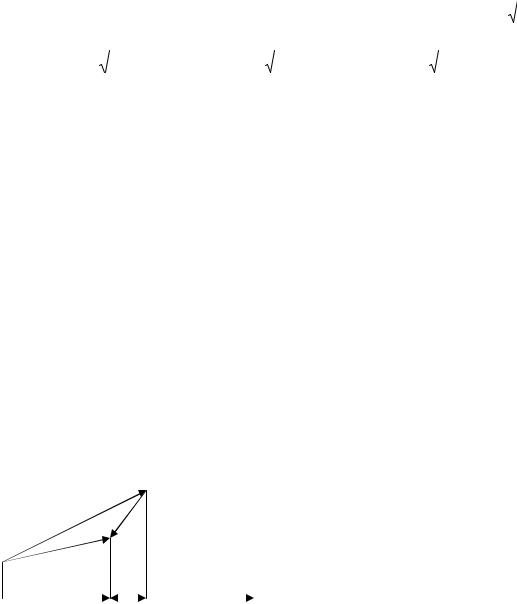
|
OA |
= |
x |
i |
= |
x |
, |
OB |
= |
y |
|
j |
= |
y |
, |
OC |
= |
z |
k |
= |
z |
, где |
x |
, |
y |
, |
z |
- |
абсолютные величины |
||||
чисел. Если вектор |
|
совпадает по направлению с |
осью OX , |
|
x > 0 . В |
||||||||||||||||||||||||||||
OA |
то |
||||||||||||||||||||||||||||||||
противном случае: x < 0 . |
Таким |
|
образом |
|
знак |
x |
совпадает |
со |
знаком |
||||||||||||||||||||||||
алгебраической проекции |
прOX d , |
то есть |
x = прOX d . |
Аналогично: y = прOY d , |
|||||||||||||||||||||||||||||
z = прOZ d . доказательство завершено.
Обозначим α , β ,γ |
- углы наклона вектора d к осям координат соответственно |
||||||||||||||||||||||||||||||||||||
OX ,OY ,OZ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Направляющими косинусами |
|
вектора |
|
d |
называются три |
числа |
|||||||||||||||||||||||||||||||
cosα , cos β , cosγ . Из рисунка теоремы 8.2 можно записать x = |
|
d |
|
cosα , |
|
y = |
|
d |
|
cos β , |
|||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
z = |
|
|
|
cosγ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
. |
||||||||||||
|
d |
|
Поскольку |
d |
- |
диагональ параллелепипеда, то |
|
|
|
d |
|
|
x2 + y2 + z2 |
||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Тогда: cosα = |
|
|
x |
|
|
, |
cos β |
= |
|
|
y |
|
, |
cosγ = |
|
|
|
|
|
z |
|
. Отсюда |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
x2 |
+ y2 |
+ z2 |
x2 |
+ y2 + z2 |
x2 + y2 + z2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
получаем |
свойство |
|
|
направляющих |
|
косинусов |
|
|
|
вектора |
|
d : |
|||||||||||||||||||||||||
cos2 α + cos2 β + cos2 γ = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Теорема 8.3. (справедлива для геометрических и алгебраических проекций)
1)Проекция суммы двух векторов на некоторую ось u равна сумме проекций этих векторов на ось u .
2)Проекция на некоторую ось u произведения вектора на
вещественное число равна произведению числа на проекцию этого вектора на ось u .
Доказательство. Совместим ось u с декартовой системой координат – осью
OX . |
Пусть два |
вектора |
заданы |
своими координатами: d1 = x1i + y1 j + z1k , |
|||||||||||||
d2 = x2i + y2 j + z2k . Тогда d1 + d2 = (x1 + x2 )i + ( y1 + y2 ) j + (z1 + z2 )k , |
|
||||||||||||||||
αd1 = αx1i + αy1 j + αz1k . |
Из этих соотношений видно, |
что прu d1 = x1 , прu d2 = x2 , |
|||||||||||||||
прu (d1 + d2 ) = x1 + x2 , |
прu (αd1) = αx1 . |
Поэтому справедливы |
следующие |
||||||||||||||
соотношения: прu (d1 + d2 ) = x1 + x2 |
= прu d1 + прu d2 , прu (αd1 ) = αx1 = αпрu (d1 ) . |
||||||||||||||||
|
|
|
|
|
|
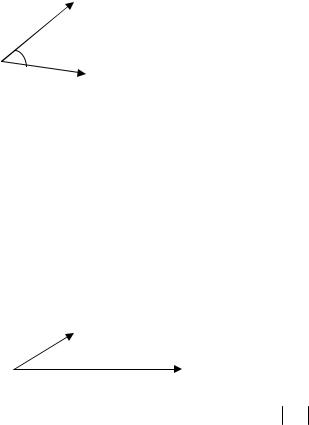
8.1.Пусть |
|
|
вектора |
|
|
|
. |
|
их сумму: |
||
Пример |
даны |
два |
AB, |
BC |
Рассмотрим |
||||||||||||
|
|
+ |
|
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
AB |
BC |
AC |
|
|
|
|
|
|
|
|
|
|
||||
B
C
A
u
A' C' B'
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из |
|
рисунка |
видно, |
|
что |
|
A 'B' + B 'C' = A 'C' . |
То |
есть |
||||||||||
Прu |
|
+ Прu |
|
= Прu |
|
= Прu ( |
|
+ |
|
) . |
Кроме того, прu AB > 0 , |
прu BC < 0 , |
|||||||
AB |
BC |
AC |
AB |
BC |
|||||||||||||||
поэтому прu AB + прu BC = прu AC . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3
Скалярное произведение двух векторов
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначается (a,b). Таким |
образом (a,b) = |
|
a |
|
|
|
b |
|
cosϕ . |
Между |
векторами два |
||||||||||
|
|
|
|
||||||||||||||||||
угла: ϕ и π − ϕ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Договоримся считать углом между векторами угол, |
меньший π . Если ϕ = π , |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
то векторы называются ортогональными. |
|
|
|||||||||||||||||||
Обозначим: прab = |
|
a |
|
cosϕ , |
прb a = |
|
b |
|
cosϕ . Отсюда |
следует |
эквивалентное |
||||||||||
|
|
|
|
||||||||||||||||||
определение скалярного произведения:
Скалярным произведением двух векторов называется число, равное произведению длины одного из этих векторов на проекцию другого вектора на ось, ориентированную по первому вектору.
Физический смысл скалярного произведения
F
O |
ϕ |
A |
a |
Пусть a - смещение материальной точки O , F - сила, действующая на точку O . Тогда (a, F ) - работа силы F : (a, F ) = a
 F cosϕ .
F cosϕ .
Геометрические свойства скалярного произведения
Теорема 8.4.
Два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.
( ) |
a и b ортогональны. Следовательно: ϕ = π |
и cosϕ = 0 . Тогда (a,b) = 0 . |
|
2 |
|
(Ü) |
(a,b) = 0 , если a = 0 или b = 0 или cosϕ = 0 . |
|
|
Если a = 0 или b = 0 , то, поскольку у |
нулевых векторов считается |
направление произвольное, то можно считать, что a ^ b .
Если a ¹ 0 и b ¹ 0 , то cosϕ = 0 и тогда ϕ = π .
2
Теорема 8.5.
Два ненулевых вектора образуют :
1.острый угол между собой тогда и только тогда, когда (a,b) > 0 ;
2.тупой угол между собой тогда и только тогда, когда (a,b) < 0 .
4

Алгебраические свойства скалярного произведения
1. (a,b) = (b, a)
Доказательство: (a,b) = a
 b cosϕ = b
b cosϕ = b
 a cosϕ = (b, a)
a cosϕ = (b, a)
2. (αa,b) = α (b, a)
Доказательство: (αa,b) = b прb (αa) = α b прb (a) = α (a,b)
3. (a + b, c) = (a, c) + (b, c)
Доказательство: (a + b, c) = |
|
c |
|
прc (a + b) = |
|
c |
|
прc (a) + |
|
c |
|
прc (b) = (a, c)+ (b, c) |
|||||
|
|
|
|
|
|
||||||||||||
4. (a, a) = |
|
a |
|
2 |
> 0, если |
|
|
|
a ¹ 0 |
||||||||
|
|
|
|
|
|||||||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
= 0, если |
|
|
|
a = 0 |
||||||||
|
|
|
|
|
|
|
|
||||||||||
Выражение скалярного произведения в декартовой системе координат
Пусть заданы два вектора: a = {x1, y1, z1}, b = {x2 , y2 , z2 }.
Теорема 8.6.
В декартовой системе координат скалярное произведение двух векторов равно сумме парных произведений соответствующих координат:
(a,b) = x1x2 + y1 y2 + z1z2 .
Доказательство:
(a,b) = (x1i + y1 j + z1k, x2i + y2 j + z2k ) = x1x2 (i,i) + x1 y2 (i, j) + x1z2 (i, k ) + y1x2 ( j,i) + y1 y2 ( j, j) + y1z2 ( j, k )+ z1x2 (k,i) + z1 y2 (k, j) + z1z2 (k, k ).
Поскольку согласно четвертому свойству: (i,i) = 1,( j, j) = 1,(k, k ) = 1, а по теореме 8.4. из ортогональности векторов : (i, j) = 0, (i, k ) = 0,( j,i) = 0 , ( j, k ) = 0, (k,i) = 0,(k, j) = 0 , то
последняя сумма равна x1x2 + y1 y2 + z1z2 . Таким образом получили:
(a , b ) = x1 x2 + y1 y 2 + z1 z 2 .
Следствие 1.
Два вектора ортогональны тогда и только тогда, когда x1x2 + y1 y2 + z1z2 = 0 ,
где a = {x1, y1, z1}, b = {x2 , y2 , z2 }.
Следствие 2. Если a = {x1, y1, z1}, b = {x2 , y2 , z2 }, то угол между ними вычисляется
по формуле cosϕ = |
|
|
x1x2 + y1 y2 + z1z2 |
|
||||
|
|
|
|
|
|
|
|
|
x2 |
+ y2 |
+ z2 |
|
x2 |
+ y2 |
+ z2 |
||
|
|
|
||||||
1 |
1 |
1 |
2 |
2 |
2 |
|||
5
