Lektsii_PDF / Лекция_7

Лекция № 7

Понятие базиса

Базисом на прямой называется любой ненулевой вектор.

Базисом на плоскости называются два неколлинеарных вектора, взятых в определенном порядке.

Базисом в пространстве называются три некомпланарных вектора, взятых в определенном порядке.

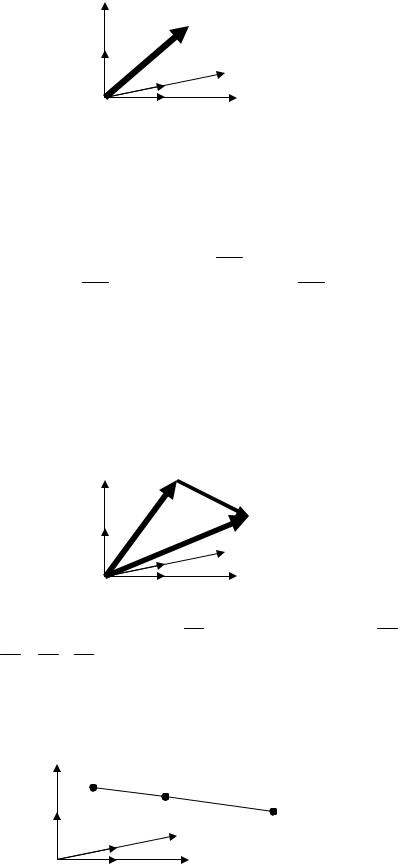
Так как любой вектор d раскладывается в линейную комбинацию трех некомпланарных векторов a,b, c , то можно записать: d = αa + βb + γc . При этом само выражение называется разложением вектора d по базису a,b, c . Числа α , β ,γ называются координатами вектора d относительно базиса a,b, c . таким

образом, любому вектору d ставится в соответствие упорядоченная тройка

(α , β ,γ ).

Теорема 7.1

1)Координаты суммы двух векторов d1 + d2 в некотором базисе равны суммам координат этих векторов в том же самом базисе. (При сложении векторов складываются координаты)

2)Координаты произведения вектора на число λd1 в некотором

базисе равны произведению координат этого вектора на вещественное число.

(При умножении вектора на число умножаются его координаты)

Декартовые прямоугольные координаты

Аффинной системой координат называется совокупность точки и базиса. Точка называется началом координат.

Координаты вектора в базисе, состоящем из трех линейно-независимых векторов, называется аффинными координатами.

Если векторы a,b, c взаимно-ортогональны и по длине равны 1, то получается частный случай аффинной системы координат, называемой декартовой системой координат. ЕЕ базис – три ортонормированных вектора i, j, k : i = j = k = 1 и i j, j k,i k . В базисе i, j, k любой вектор имеет

1

разложение по базису: d = xi + yj + zk , где x, y, z называются декартовыми координатами вектора d . Обозначается d = {x, y, z}.

координат и совпадающие по направлению с ортами, называются осями координат: OX - ось абсцисс, OY- ось ординат, OZ- ось аппликат.

Плоскости, проходящие через оси, называются координатными плоскостями: Oxy, Oyz, Oxz.

Пусть задан вектор OM . Пусть его координаты {x, y, z}. Тогда можно записать: OM = xi + yj + zk . А вектор OM называется радиус-вектором точки

M (x, y, z) .

Нахождение координат вектора при известных значениях координат его начала и конца.

Если у вектора известны координаты его начала и конца, то для нахождения координат вектора необходимо из координат его конца вычесть координаты его начала. Проиллюстрируем сказанное.

Z A(x1, y1, z1 )

B(x2 , y2 , z2 )

Пусть OA = {x1, y1, z1}, OB = {x2 , y2 , z2 }. Тогда

AB = OB − OA = {x2 − x1, y2 − y1, z2 − z1}.

Деление отрезка в заданном отношении.

Пусть точки A и B заданы своими координатами:

Z A(x1, y1, z1 )

2

λ > 0, μ > 0 . Следовательно, можно записать: μ AM = λ MB . Если векторы равны,

то равны и их координаты тоже:

μ(x − x1 ) = λ(x2 − x) μ(y − y1 ) = λ(y2 − y) μ(z − z1 ) = λ(z2 − z)

радианах).

однозначности выбирают угол − π < ϕ ≤ π , который называется главным.

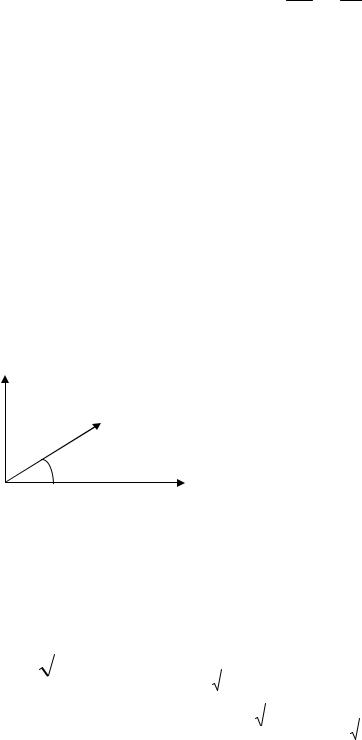
Пример 7.1. Какую линию описывает следующее уравнение: r = 2a sinϕ ? Решение. Используя формулы для прямоугольного треугольника, можно

3

Y

a

X

Цилиндрическая и сферическая системы координат

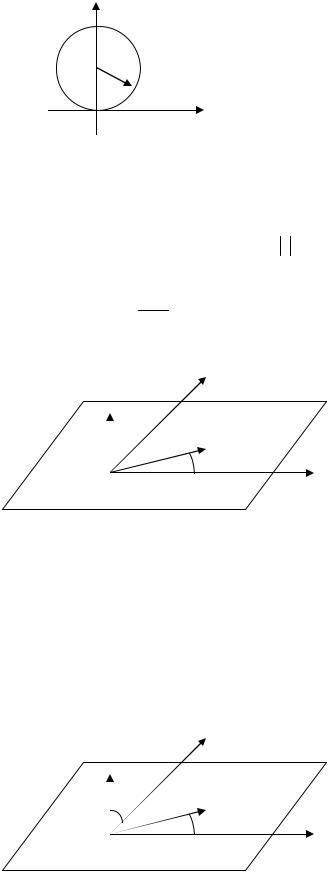
Эти системы координат являются обобщением полярной системы. Содержит т. O , луч l из точки O , вектора n : n = 1 , n l , плоскость P n .

Цилиндрические координаты точки M - это (r,ϕ, h), где r - радиус-

вектор точки M ' (как проекции точки M на плоскость P ), угол ϕ - угол между вектором OM ' и осью l , h - координата точки M по вектору n .

M

Если совместить цилиндрическую и декартовую системы координат таким образом, чтобы начала координат совпали, ось X совпадала по направлению с полярной осью, ось Z совпадала по направлению с вектором

Если совместить сферическую и декартовую системы координат таким образом, чтобы начала координат совпали, ось X совпадала по направлению

4