Lektsii_PDF / Лекция_9

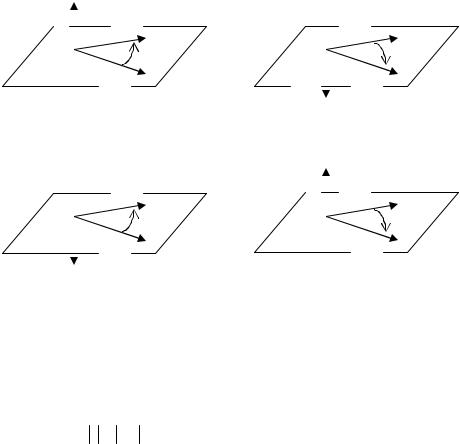
Лекция № 9

Векторное произведение двух векторов

Три вектора называются упорядоченной тройкой (просто тройкой),

если указано: какой из этих векторов является первым, какой вторым, какой третьим.

Упорядоченность векторов будем отражать порядком их следования или написания.

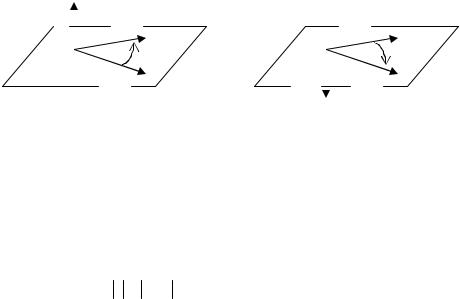
Тройка некомпланарных векторов a,b, c образует правую (левую) тройку, если выполняется одно из условий:

1.если после приведения их к общему началу вектор c расположен по ту сторону от плоскости, содержащей вектора a и b , откуда кратчайший поворот от вектора a к вектору b совершается против (по) часовой стрелке.

2.если после приведения их к общему началу, эти векторы располагаются так, как расположены соответственно большой, указательный и средний палец правой (левой) руки:

a)правая тройка: если abc правая, то ,bca, cab тоже правая.

b) левая тройка: если abc левая, то ,bca, cab тоже левая.

Декартовая система координат называется правой, если векторы i , j , k образуют правую тройку, левой, если векторы i , j , k образуют левую тройку.

Векторным произведением вектора a на вектор b называется вектор c (обозначается c = [a,b]), который удовлетворяет следующим условиям:

c)c = ab sinϕ , где ϕ - угол между векторами a и b ;

d)векторc ортогонален векторамa и b ;

1

e) векторы a , b , c образуют правую тройку.

Геометрические свойства векторного произведения

Теорема 9.1.

Два вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулю.

Теорема 9.2.

Длина вектора c = [a,b] равна площади S параллелограмма,

построенного на векторах a , b , приведенных к общему началу:

S = c = [a,b] .

Ортом e ненулевого вектора c называется единичный вектор, коллинеарный с вектором c и имеющий с вектором c одинаковое направление:

[a,b] = Se , где e - орт вектора c .

Алгебраические свойства векторного произведения

1.[a,b] = −[b, a]

2.[αa,b] = α[a,b]

3.[a + b, c] = [a, c]+ [b, c]

4.[a, a] = 0 a

Выражение векторного произведения в декартовой системе координат

Пусть заданы два вектора: a = {x1, y1, z1}, b = {x2 , y2 , z2 }.

Теорема 9.3.

В декартовой системе координат векторное произведение двух векторов вычисляется с помощью следующего выражения:

Используя определение векторного произведения и понятия правой тройки, запишем следующие соотношения:

2

Используя 2 и 3 алгебраические свойства векторного произведения или другими словами «раскрывая скобки и вынося множитель за скобки», а также последние равенства, получим:

c = [a,b] = (y1z2 − z1 y2 )i + (z1x2 − x1z2 ) j + (x1 y2 − y1x2 )k = {y1z2 − z1 y2 , z1x2 − x1z2 , x1 y2 − y1x2 }

Доказательство завершено.

Следствие1. Векторное произведение двух векторов, заданных своими координатами равно:

Следствие 2. Два вектора коллинеарны тогда и только тогда, когда пропорциональны их декартовые координаты:

Пусть даны векторы a,b, c .

Если вектор a векторно умножить на b , а полученный вектор [a,b] скалярно умножить на вектор c , то полученное число ([a,b], c) называется смешанным произведением трех векторов.

Геометрический смысл смешанного произведения

Теорема 9.4.

Смешанное произведение трех векторов ([a,b], c) равно объему параллелепипеда, построенному на векторах a,b, c , приведенных к общему началу, взятому со знаком «+», если a,b, c - правая тройка, «-» - если левая.

Следствие 1. Справедливо равенство: ([a, b], c) = (a, [b, c]) .

Доказательство: Согласно свойству коммутативности скалярного произведения можно записать: (a,[b,c]) = ([b, c], a).

Однако ([b, c], a) = ([a,b], c), поскольку:

3

1.эти смешанные произведения представляют собой объемы параллелепипеда, построенного на одних и тех же векторах.

2.тройки имеют одну и туже ориентацию, поскольку известно, что если тройка a,b, c - правая, то и b, c, a - правая, если a,b, c - левая, то и b, c, a -

левая. Поэтому знаки объемов совпадают.

Опираясь на доказанное свойство, будем использовать обозначение: (a,b, c) .

Следствие 2. Смешанное произведение трех векторов a,b, c равно нулю, если все векторы компланарны или два из них совпадают.

Алгебраические свойства

1.(a,b, c) = (b, c, a) = (c, a,b) = −(c,b, a) = −(b, a, c) = −(a, c,b)

2.((a + b), c, d ) = (a, c, d )+ (b, c, d )

3.α (a,b, c) = (αa,b, c)

Выражение смешанного произведения трех векторов в декартовой системе координат

Пусть заданы три вектора: a = {x1, y1, z1}, b = {x2 , y2 , z2 }, c = {x3 , y3 , z3}

Теорема 9.5.

В декартовой системе координат смешанное произведение трех векторов вычисляется с помощью следующего выражения:

x3 y3 z3

Доказательство: Вычисляя векторное произведение [a,b] в соответствии с формулой (9.1) получим:

c = [a,b] = {y1z2 − z1 y2 , z1x2 − x1z2 , x1 y2 − y1x2 }

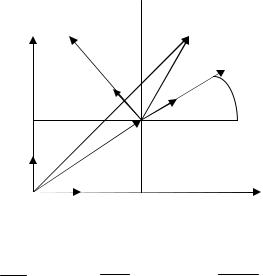
Преобразование декартовой системы координат на плоскости

Пусть на плоскости заданы две декартовые системы координат: Oij и O i' 'j' , и точка M , которая в базе ij имеет координаты M (x, y) , а в базе i 'j' - координаты

4

M

начало координат точка O' имеет координаты O'(α , β ) в базисе ij . Используя исходные условия можно записать следующие равенства:

OM = xi + yj , O'M = x 'i' + y 'j', OO ' = α i + β j .

Любой вектор можно разложить по базису, в том числе векторы i' и j':

Разложение любого вектора по любому базису является единственным,

Теперь найдем неизвестные коэффициенты α11,α12 ,α21,α22 :

1.Рассмотрим случай, когда 1 и 2 системы одной ориентации, то есть, когда одна получается из другой переносом начала координат и поворотом координатных осей на угол ϕ .

Умножим последовательно каждое соотношения (9.5) скалярно на i и j : получим:

(i',i)= α11 (i,i) + α12 ( j,i) = α11 , поскольку (i,i) = 1 , (i, j) = 0 . С другой стороны согласно определению скалярного произведения:

(j', j) = α22 = cos Ðj' j

5

В результате имеем:

2. Рассмотрим случай, когда система разной ориентации.

В результате имеем:

Можно сделать обратные преобразования, выразив из соотношений (9.7) и (9.8) переменные x ', y' :

1) для систем одинаковой ориентации из (9.7) получим:

x' = (x - α ) cosϕ + ( y - β )sinϕ y' = -(x - α )sinϕ + ( y - β ) cosϕ

2)для систем разной ориентации из (9.8):

x' = -(x - α ) cosϕ - ( y - β )sinϕ

y' = -(x - α )sinϕ + ( y - β ) cosϕ

6