2.2. Согласованный фильтр

Пусть на вход фильтра поступает рассмотренный в предыдущем параграфе сигнал S(t).

Сигнал на выходе фильтра определяется интегралом Дюамеля, т.е. является сверткой функции S(t) и импульсного отклика g(t).

. (2.2)

Зафиксируем момент времени t₀ и выберем импульсную характеристику g(t) такой, чтобы в этот момент времени выходной сигнал U_ВЫХ(t) принимал максимальное значение.

Неравенство Коши-Буняковского применительно к (2.2) имеет вид:

. (2.3)

При этом выходной сигнал U_ВЫХ(t₀) в момент времени t₀ принимает максимальное значение при условии:

Заменой переменных t = t₀ - τ получаем требуемое значение импульсной характеристики согласованного фильтра:

(2.4)

В соответствии с (4.4) импульсная характеристика согласованного фильтра представляет собой с точностью до постоянной «зеркальную» копию входного сигнала S(t), сдвинутую на время t₀.

На рис. 2.2 показано построение импульсной характеристики согласованного фильтра. Ясно, что момент времени t₀, при котором достигается максимум U_ВЫХ(t), не может быть менее, чем длительность импульса Т. В противном случае импульсная характеристика g(t) будет отлична от нуля при t < 0, т.е. импульсный отклик на выходе фильтра появится раньше, чем на его вход поступит d - импульс.

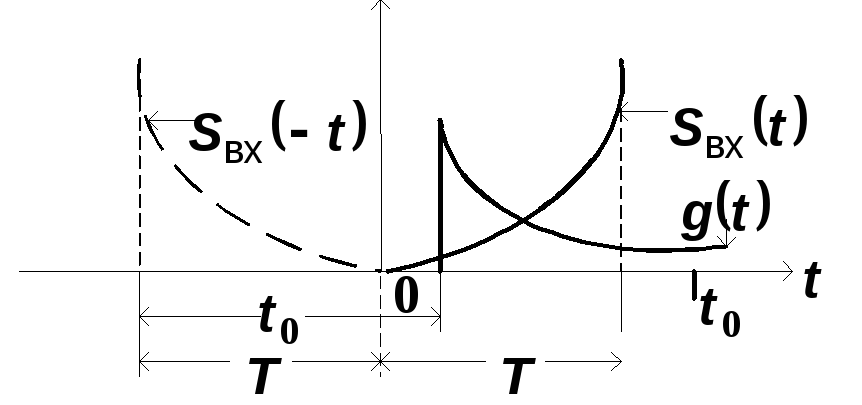
Рис. 2.2. Иллюстрация к порядку построения импульсной характеристики

Запишем (24) в виде выражения и подставим его в (2.2):

. (2.5)

Интеграл в (2.5) представляет собой автокорреляционную функцию сигнала S(t), сдвинутую во времени на величину t₀.

Окончательное выражение для сигнала на выходе согласованного фильтра имеет вид:

. (2.6)

Таким образом, если в приёмнике используется оптимальный фильтр, согласованный с сигналом, то сигнал на его выходе представляет собой с точностью до постоянной автокорреляционную функцию входного сигнала, сдвинутую во времени на величину t₀. Обычно этот момент времени совпадает с моментом окончания импульсного сигнала, т.е. t₀ = T.

Автокорреляционная функция, а, следовательно, сигнал на выходе оптимального фильтра, имеет несколько максимумов; наибольший из них B_S(0), соответствующий моменту времени t₀ = T , равен энергии сигнала. В этот же момент времени выходной сигнал достигает максимума и происходит сравнение выходного сигнала с опорным сигналом.

В цифровой системе передачи логической единице соответствует прямоугольный импульс сигнала положительной полярности, а логическому нулю – отрицательной полярности. В этих системах реализуется принцип поэлементного приёма сигналов. Это значит, что приёмник принимает решение отдельно по каждому элементу цифрового потока, т.е. по каждому прямоугольному импульсу положительной или отрицательной полярности.

Определим функцию автокорреляции и вид сигнала на выходе оптимального приёмника, когда на его вход поступает прямоугольный импульс S(t) длительностью T:

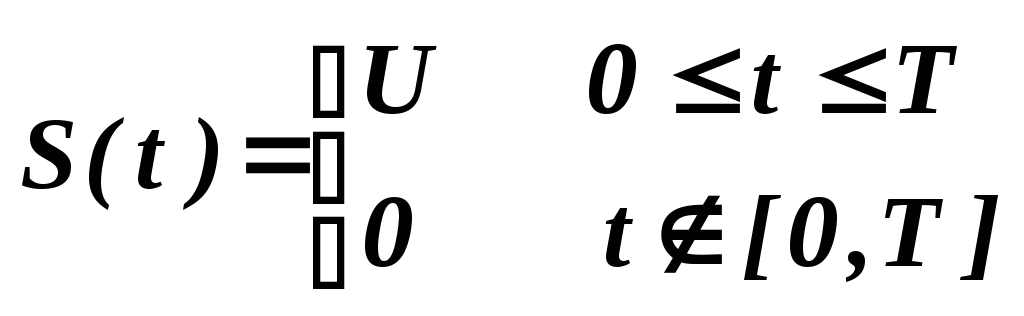
Вычисление автокорреляционной функции иллюстрируется рис. 2.3.

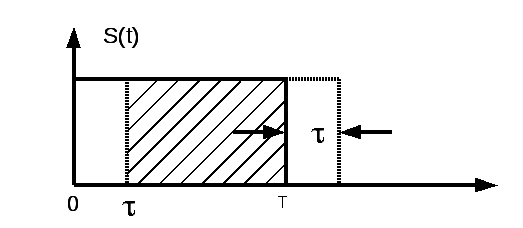
Рис. 2.3 Иллюстрация к выводу формулы

Пусть первоначально. Проведём преобразования:

.

Так как функция автокорреляции чётная, то есть выполняется условие , то для всех значений τ функция автокорреляции имеет вид, представленный на рис. 2.4:

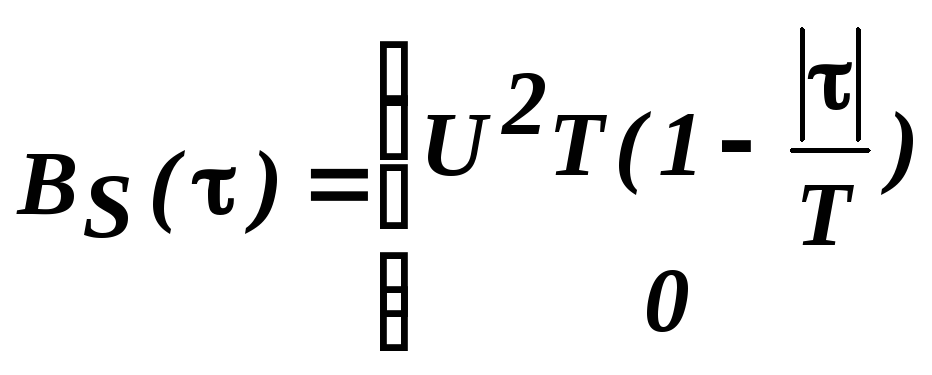
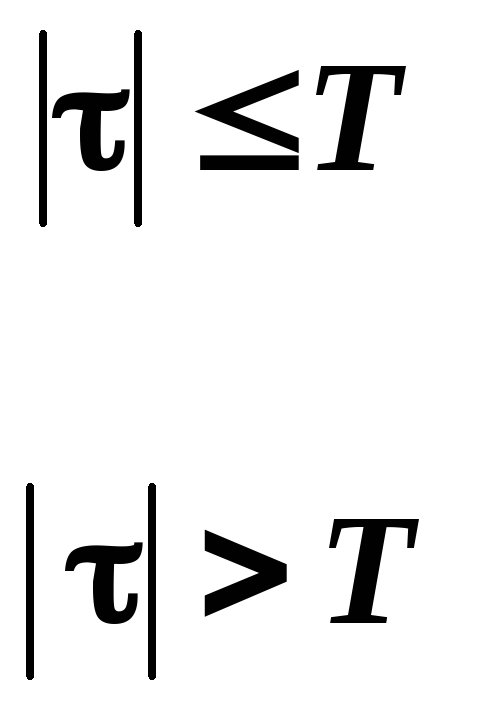
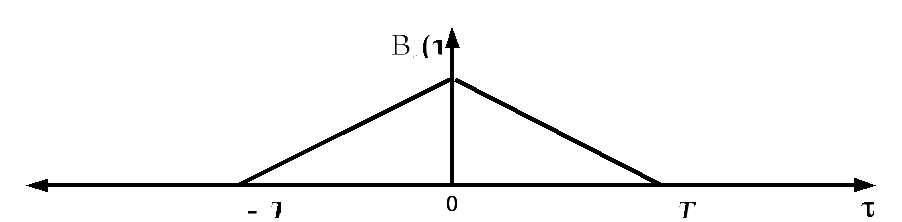
Рис. 2.4 Функция автокорреляции

Сигналом на выходе является сдвинутая на время T функция автокорреляции:

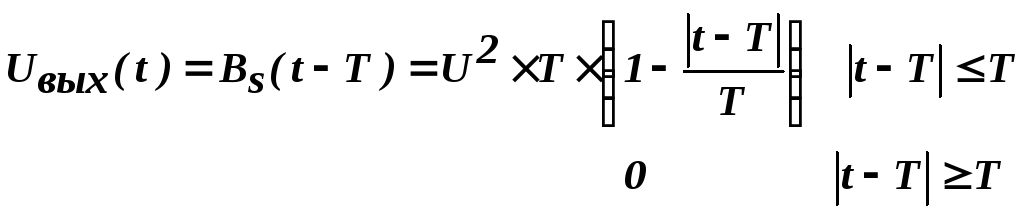
График сигнала U_вых(t) на выходе оптимального приёмника представлен на рис.2.5.

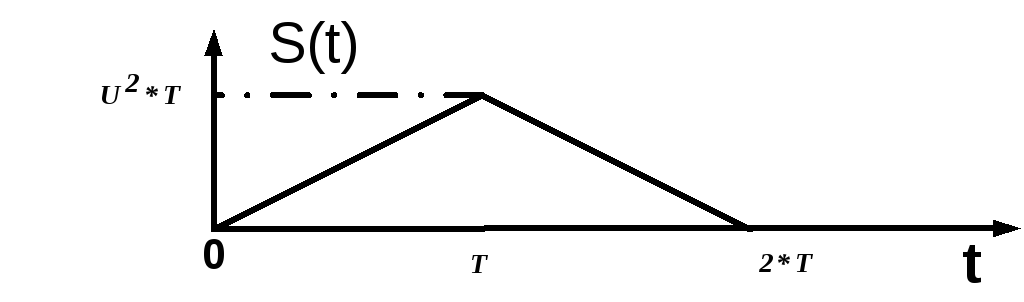
_{Рис. 2.5 Сигнал на выходе оптимального приёмника}