
Zaslavky-Akopyan
.pdf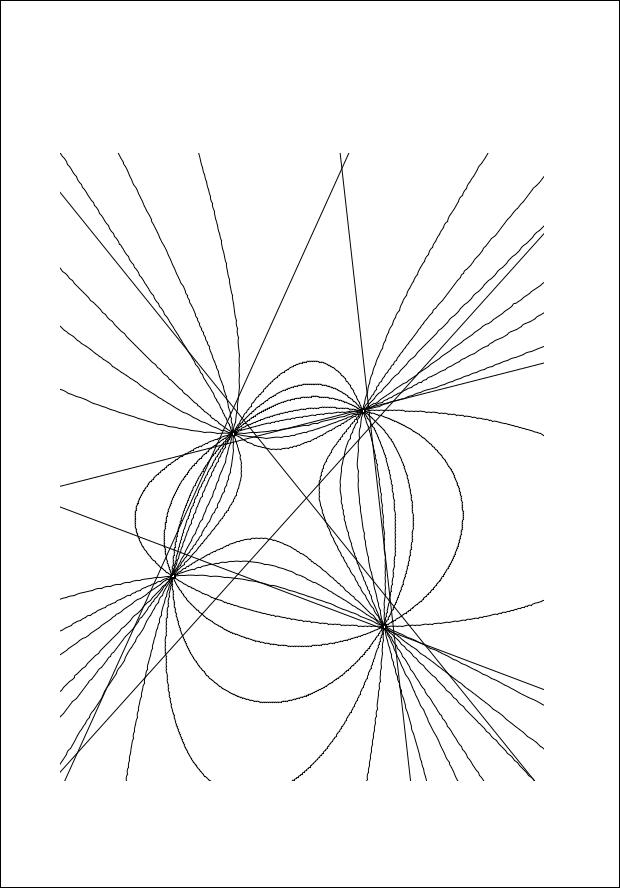
§ 3.3. Пучки кривых. Теорема Понселе |
81 |
1. Пучки, проходящие через четыре различные точки (рис. 3.20). |
|
Этому типу принадлежат также эллиптический и гиперболический |
|
пучки окружностей. |
|
Рис. 3.20 |
|
82Глава 3. Проективные свойства коник
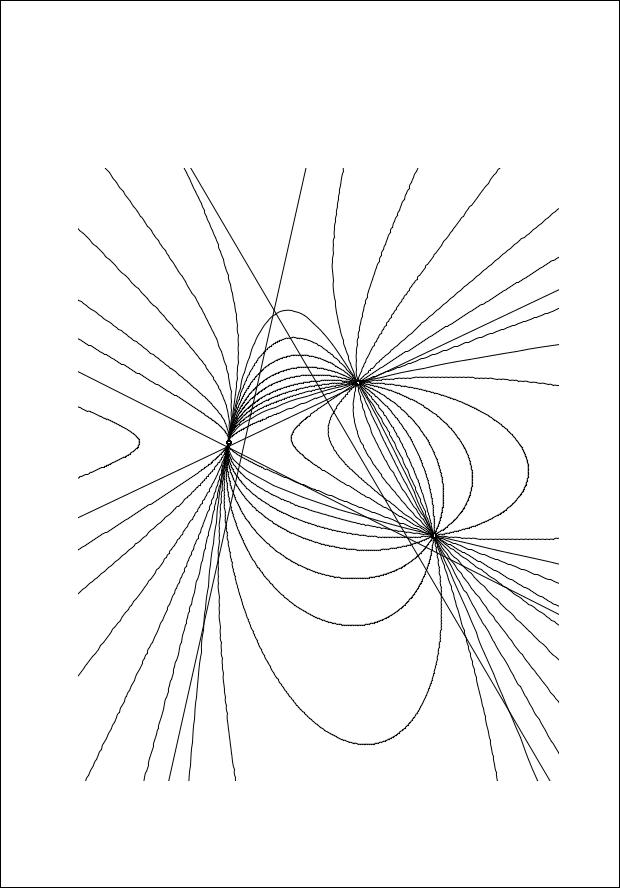
2.Пучки, проходящие через четыре точки, две из которых совпадают, т. е. касающиеся данной прямой в фиксированной точке (рис. 3.21). Параболический пучок окружностей принадлежит этому типу.
Рис. 3.21

§ 3.3. Пучки кривых. Теорема Понселе |
83 |
3. Пучок, у которого две пары точек склеиваются. Он будет со- |
|
стоять из коник, касающихся двух данных прямых в двух данных |
|
точках (рис. 3.22). К этому типу также принадлежит пучок концен- |
|
трических окружностей или парабол, уравнение которых имеет вид |
|
y = ax2. |
|
Рис. 3.22 |
|

84Глава 3. Проективные свойства коник
4.Пучок, у которого три точки сливаются в одну (рис. 3.23). Коники этого пучка соприкасаются с некоторой окружностью.
Рис. 3.23
5. Сверхсоприкасающийся пучок, у которого четыре точки, определяющие пучок, совпадают (рис. 3.24). Пример такого пучка – параболы, уравнение которых имеет вид y = x2 + a.

§ 3.3. Пучки кривых. Теорема Понселе |
85 |
Рис. 3.24 |
|
Помимо пучков, заданных четырьмя точками, можно рассматри- |
|
вать двойственные пучки, т. е. множества коник, касающихся че- |
|
тырех данных прямых (рис. 3.25–3.27). Двойственные пучки также |
|
классифицируются в зависимости от того, есть ли среди определяю- |
|
щих пучок прямых совпадающие. Если совпадают две прямые, то все |
|
коники пучка касаются их, а значит, и друг друга, в одной точке; |
|
если три, то коники пучка соприкасаются; если все четыре, то сверх- |
|
соприкасаются. Отметим, что дважды касающийся и сверхсоприка- |
|
сающийся пучки являются самодвойственными, т. е. переходят са- |
|
ми в себя при полярном соответствии относительно любой входящей |
|
в пучок коники. Пользуясь принципом двойственности, можно для |
|
каждого утверждения об обычных пучках сформулировать соответ- |
|
ствующее утверждение о двойственных и наоборот. |
|
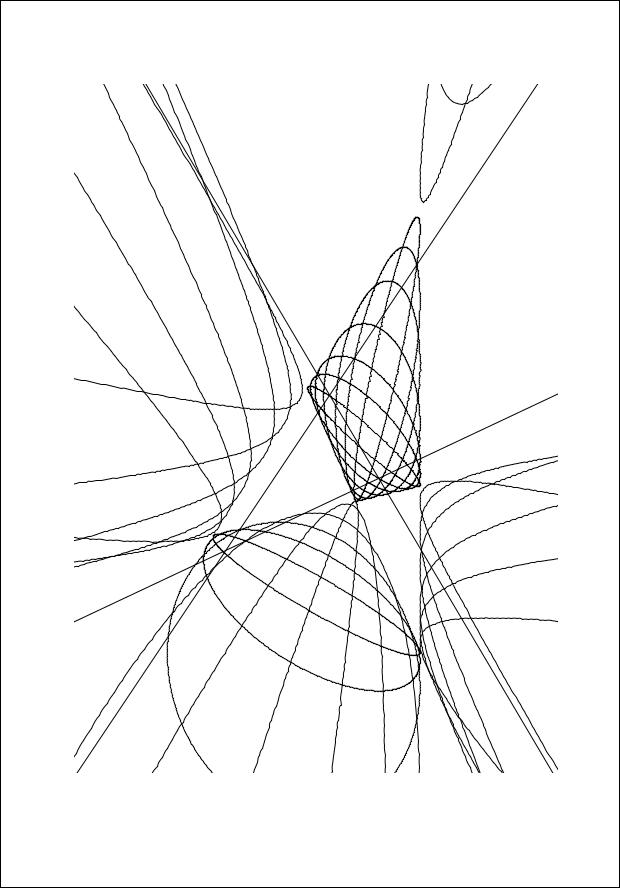
86 Глава 3. Проективные свойства коник |
Рис. 3.25 |
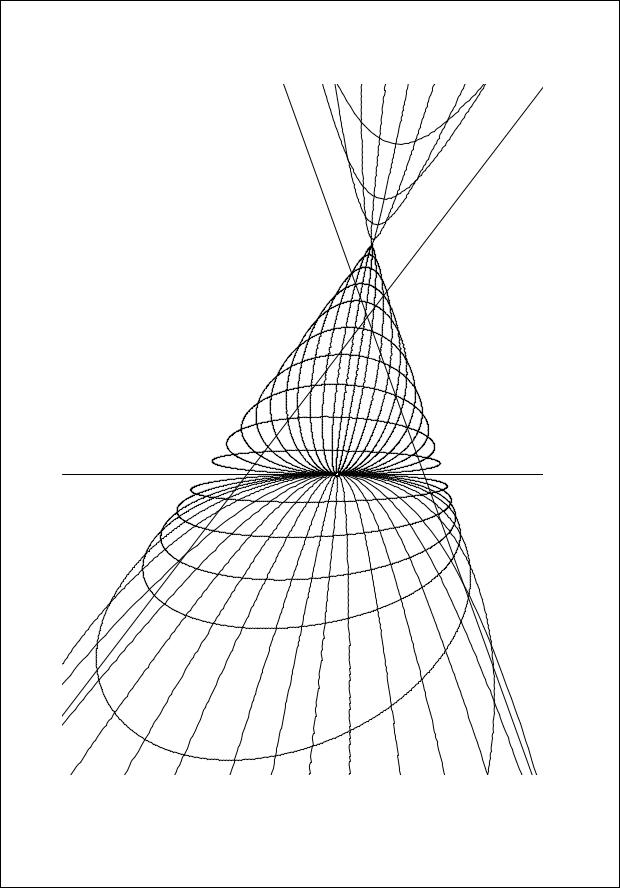
§ 3.3. Пучки кривых. Теорема Понселе |
87 |
Рис. 3.26 |
|

88 Глава 3. Проективные свойства коник |
Рис. 3.27 |
§ 3.3. Пучки кривых. Теорема Понселе |
89 |
С помощью теоремы о пучке коник можно доказать следующий красивый факт.
a Теорема 3.11 (о четырех кониках). Пусть даны три коники a1,
2, a3, и пусть P1, Q1, P1′ , Q′1 – точки пересечения коник a2 и a3; P2, Q2, P2′ , Q′2 – точки пересечения коник a1 и a3; P3, Q3, P3′ , Q′3 – точки пересечения коник a2 и a1. Тогда если точки P1, Q1, P2, Q2, P3, Q3
лежат на одной конике, то прямые P′ |
Q′ |
, P′ |
Q′ |
, P′ |
Q′ |
пересекаются |
||||
в однойa |
точке (рис. 3.28). |
|
1 |
1 |
2 |
2 |
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|||
|
P2 |
P′ |
Q1 |
|
|
|
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q2′′ |
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
Q1 |
|
′ |
P3 |
|
|
|
|
|
|
|
|
|
|
P1 |
|
|
|
|
|
|
|
Q3 |
P2′ |
|
|
|
|
|
|
|
|
|
|
Q3′ |
|
|
Q2 |
|
|
|
|
|
|
a2 |
P1 |
|
a3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Рис. 3.28 |
|
|
|
|
|
|
Рис. 3.29 |
||
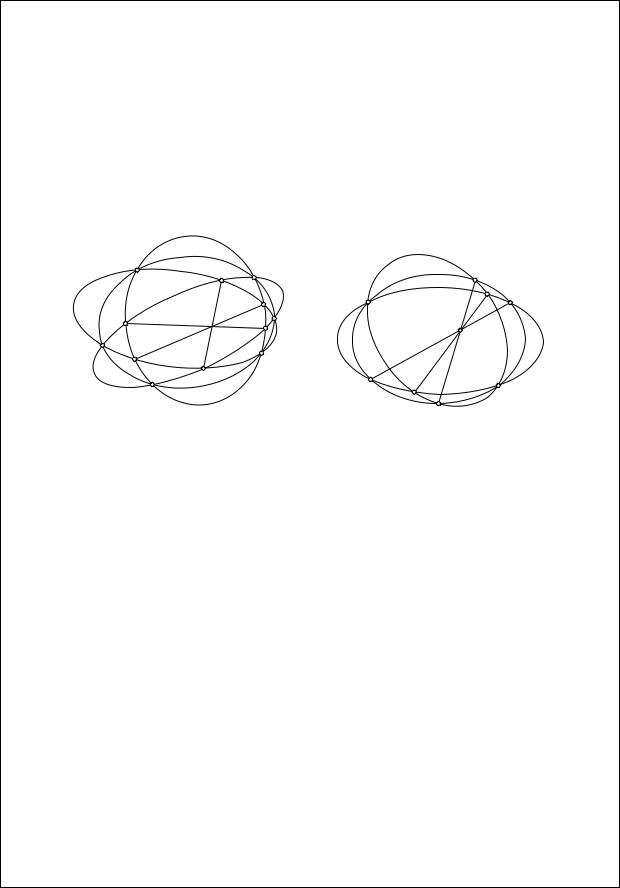
Доказательство. Докажем сначала следующее вспомогательное утверждение.
Теорема 3.12 (о трех кониках). Пусть три коники имеют две общие точки. Тогда их общие хорды, проходящие через остальные точки пересечения каждой пары, пересекаются в одной точке (рис. 3.29).
Для доказательства достаточно перевести общие точки коник в точки пересечения бесконечно удаленной прямой с окружностями. Тогда все три коники перейдут в окружности и утверждение теоремы будет следовать из существования радикального центра.
Пусть теперь a0 – коника, проходящая через точки Pi, Qi, Fi(x, y)= = 0 – уравнение коники ai. Так как вырожденная коника, состоящая из прямых P2P3 и Q2Q3, принадлежит одному пучку с a0, a1, можно считать, что ее уравнение имеет вид F0 = F1. Аналогично уравнениями коник, состоящих из прямых P1Q1, P3Q3 и P1Q1, P2Q2, будут соответственно уравнения F0 = F2 и F0 = F3. Следовательно, на всей прямой P3Q3 выполняется равенство F1 = F2. Так как оно выполнено и для точек P3′ , Q′3, оно является уравнением вырожденной коники, состоящей из прямых P3Q3 и P3′ Q′3. Соответственно, уравнением коники, состоящей из прямых P2Q2 и P2′ Q′2, будет уравнение F1 = F3, а из прямых P1Q1 и P1′ Q′1 – уравнение F2 = F3. Таким образом, эти три коники принадлежат одному пучку. Три точки, задающие этот пучок, находятся

90 Глава 3. Проективные свойства коник
изa теоремы о трех кониках, примененной к тройкам a0, a1, a2; a0, a1, 3; a0, a2, a3: это точки пересечения троек прямых P1Q1, P2Q2, P3′ Q′3;
P1Q1, P3Q3, P2′ Q′2; P2Q2, P3Q3, P1′ Q′1. Значит, четвертая точка принадлежит всем прямым Pi′Q′i. Аналогичными рассуждениями доказыва-
ется обратное утверждение: если каждая из четырех троек прямых
P1Q1, P2Q2 и P3′ Q′3; P1Q1, P3Q3 и P2′ Q′2; P2Q2, P3Q3 и P1′ Q′1; P1′ Q′1, P2′ Q′2
и P3′ Q′3 пересекается в одной точке, то точки P1, Q1, P2, Q2, P3, Q3 (а также P1, Q1, P2′ , Q′2, P3′ , Q′3 и две аналогичные шестерки) лежат на одной конике.  Воспользовавшись принципом двойственности, получаем следую-
Воспользовавшись принципом двойственности, получаем следую-
щие утверждения.
Теорема 3.13 (двойственная к теореме о трех кониках). Пусть три коники касаются двух заданных прямых. Тогда точки пересечения общих касательных, отличных от заданных прямых, к каждой паре из них лежат на одной прямой (рис. 3.30).
Рис. 3.30
Теорема 3.14 (двойственная к теореме о четырех кониках). Если две из общих касательных к каждой паре из данных трех коник касаются одной и той же коники, то точки пересечения двух других касательных к каждой паре лежат на одной прямой (рис. 3.31).
Приведем некоторые важные свойства пучков.
Теорема 3.15. Пусть A, B, C, D – четыре различные точки, X, Y, Z – точки пересечения прямых AB и CD, AC и BD, AD и BC, P – точка, отличная от X, Y, Z. Тогда поляры точки P относительно всех коник пучка, заданного точками A, B, C, D, проходят через одну
точку.
Отметим интересный частный случай. Если точки A, B, C, D образуют ортоцентрическую четверку (т. е. каждая точка является ортоцентром треугольника, образованного остальными), то полученная точка изогонально сопряжена точке P относительно треугольника
XYZ.
Действительно, поляра точки P относительно вырожденной кривой, являющейся объединением прямых AB и CD, – это прямая, сим-
