
Zaslavky-Akopyan
.pdf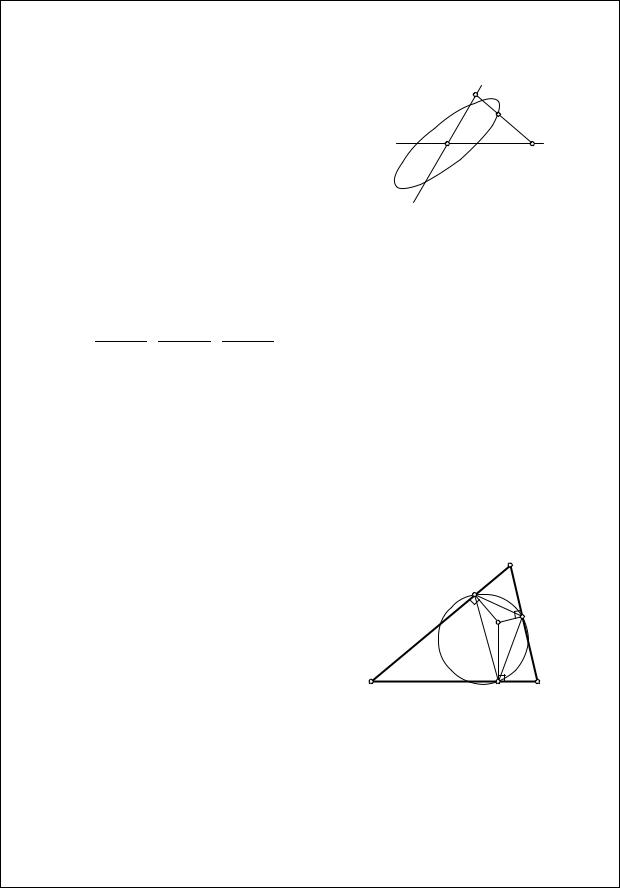
§ 2.3. Некоторые факты из геометрии треугольника |
|
41 |
||||
Задача 12. Окружности, касающиеся па- |
|
B |
||||
ры сопряженных диаметров 1 эллипса, цен- |
|
P |
||||
тры которых лежат на этом эллипсе, имеют |
|
|||||
|
|
|||||
одинаковый радиус. |
|
|
|
|
||
Задача 13. По двум пересекающимся |
A |
C |
||||
|
|
|||||
в точке A прямым скользят концы отрезка |
|
|
||||
BC, так что его длина при этом не меняет- |
|
|
||||
ся. Докажите, что если на BC зафиксировать |
Рис. 2.12 |
|||||
точку P, то ее траектория будет эллипсом |
||||||
|
|
|||||
(рис. 2.12). |
|
|
|
|
|
|
Задача 14. Пусть на сторонах треугольника ABC лежат шесть то- |
||||||
чек: A1, A2 на стороне BC, B1, B2 на стороне AC и C1, C2 на AB. До- |
||||||
кажите, что эти шесть точек лежат на одной конике тогда и только |
||||||
тогда, когда |
|
|
|
|
|
|
BA1 · BA2 · |
CB1 · CB2 · |
AC1 · AC2 = 1. |
|
|
|
|
CA1 · CA2 |
AB1 · AB2 |
BC1 · BC2 |
|
|
|
|
Предполагается, что это отношение берется со знаками. Положи- |
||||||
тельным направлением для каждого выражения полагается направ- |
||||||
ление от фигурирующей в выражении вершины в сторону другой вер- |
||||||
шины фигурирующей стороны. |
|
|
|
|||
§ 2.3. Некоторые факты из геометрии треугольника |
|
|||||
Этот параграф посвящен некоторым полезным, но не общеизвестным |
||||||
свойствам треугольника. В основном речь пойдет о свойствах изого- |
||||||
нального и изотомического сопряжений, но будет упомянут и ряд |
||||||
других красивых фактов, не имеющих |
|
|
|
|||
прямого отношения к теме книги. |
|
|
B |
|||
Определение. Педальным (подéрным) |
|
|
|
|||
треугольником точки |
P относительно |
|
|
|
||
треугольника ABC называется треуголь- |
|
|
|
|||
ник, вершинами которого являются про- |
|
|
P |
|||
екции точки P на стороны треугольника |
|
|
|
|||
ABC. Описанная окружность педального |
|
|
|
|||
треугольника называется педальной (по- |
|
|
|
|||
дерной) окружностью точки P относи- |
A |
|
C |
|||
|
|
|
||||
тельно треугольника ABC (рис. 2.13). |
|
Рис. 2.13 |
||||
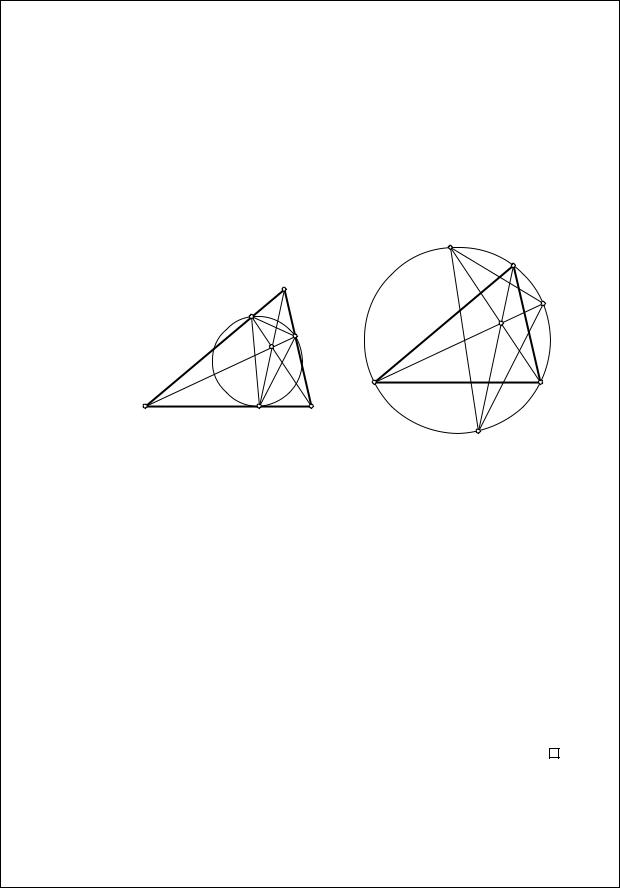
Теорема 2.6. Педальный треуголь- |
|
|||||
|
|
|
||||
ник вырождается (проекции лежат на одной прямой) точка P |
||||||
лежит на описанной окружности треугольника ABC. |
|
|||||
1.Два диаметра эллипса сопряжены, если каждый из них параллелен касательным
кэллипсу в концах другого.
42 Глава 2. Некоторые факты классической геометрии
(Это просто переформулировка леммы Симсона.)
Определение. Чевианным треугольником точки P относительно треугольника ABC называется треугольник, вершины которого – точки пересечения прямых AP и BC, BP и AC, CP и AB. Описанная окружность чевианного треугольника называется чевианной окружностью точки P относительно треугольника ABC (рис. 2.14).
Освойствах чевианных треугольников будем говорить позже.
Асейчас дадим еще определение окружностно-чевианного треуголь-
ника.
C′
B |
B
A ′ |
P
P
A C
A |
C |
|
B′ |
Рис. 2.14 |
Рис. 2.15 |
Определение. Окружностно-чевианным треугольником точки P
относительно треугольника ABC называется треугольник, вершины которого – это точки повторного пересечения прямых AP, BP, CP с описанной окружностью треугольника ABC (рис. 2.15).
Лемма 2.1. Педальный и окружностно-чевианный треугольники точки P относительно треугольника ABC подобны и одинаково ори-
ентированы.
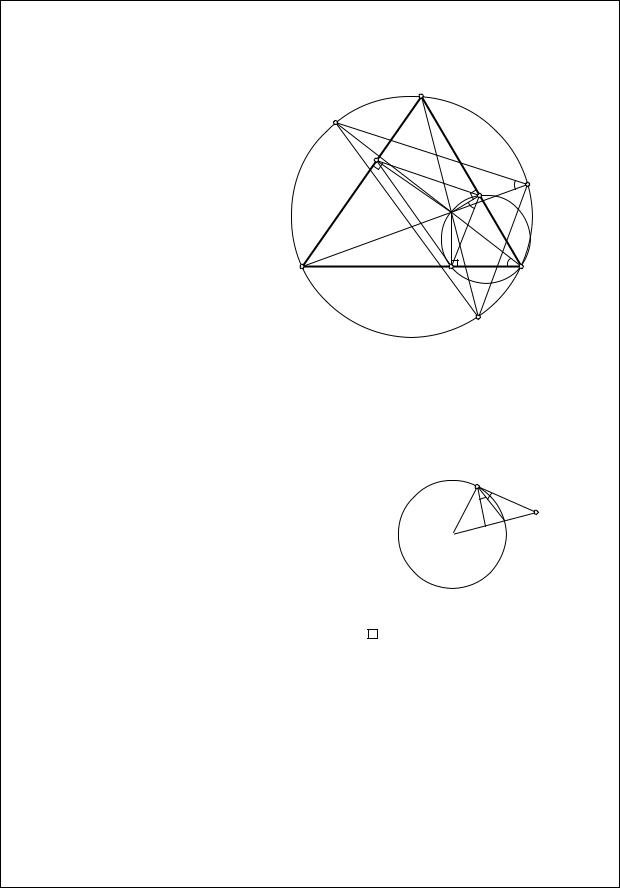
Доказательство. Рассмотрим случай, изображенный на рис. 2.16. Остальные случаи разбираются аналогично.
Точки Pa, Pb, Pc – это вершины педального треугольника, а точки A′, B′, C′ – вершины окружностно-чевианного треугольника. Мы имеем AA′C′ = ACC′ = PbPaP. Последнее равенство верно, поскольку четырехугольник PPaCPb вписанный. Аналогично доказывается, что
AA′B′ = PcPaP. А значит, C′A′B′ = PbPaPc. Аналогично A′B′C′ = = PaPbPc и A′C′B′ = PaPcPb. Но это и означает, что треугольники
A′B′C′ и PaPbPc подобны.
Теорема 2.7. Окружностно-чевианные треугольники точек, инверсных относительно описанной окружности треугольника, подобны и по-разному ориентированы.
§ 2.3. Некоторые факты из геометрии треугольника |
43 |
B
C′ |
PC
A ′ |
PA |
 P
P
A PB C
B′ |
Рис. 2.16
Сначала докажем следующую лемму.
Лемма 2.2. Пусть точки P и Q инверсны относительно окружности w с центром O. Пусть отрезок PQ пересекает w в точке R. Тогда для любой точки A, лежащей на w, RA – это биссектриса угла
PAQ.
Доказательство. Поскольку точки P и Q инверсны, треугольники OAP и OQA подобны (рис. 2.17), следовательно, OQA = = OAP. Поскольку O – центр окружности w, треугольник AOR равнобедренный, а значит,OAR = ORA. Таким образом,
A

 P
P  R Q O
R Q O
PAR = OAR − OAP = |
|
= ORA − OQA = RAQ, |
Рис. 2.17 |
что и требовалось доказать.
Из доказанной леммы следует, что окружность w является геометрическим местом точек, отношение расстояний от которых до P и Q постоянно (и отлично от 1). Она называется окружностью Аполлония отрезка PQ. О ней будет подробнее написано ниже.
Доказательство теоремы. Пусть точки P и Q инверсны относительно описанной окружности треугольника ABC (обозначим ее через w). Пусть отрезок PQ пересекает w в точке R. Обозначим повторную точку пересечения прямой AP с w через A′, а прямой AQ – через A′′. Ввиду леммы 2.2 прямая AR – биссектриса угла PAQ, следовательно, R делит дугу A′A′′ пополам, т. е. точки A′ и A′′ симметрич-

44 Глава 2. Некоторые факты классической геометрии |
|
||
ны относительно OP. То же верно для пар точек B′ и B′′, C′ и C′′, вер- |
|||
шин окружностно-чевианных треугольников точек P и Q относитель- |
|||
но треугольника ABC. Таким образом, при симметрии относительно |
|||
PQ треугольники переходят друг в друга, а значит, они подобны и по- |
|||
разному ориентированы. |
|
|
|
Следствие. Педальные треугольники инверсных точек подобны |
|||
и по-разному ориентированы. |
|
|
|
Можно показать, что для любого треугольника XYZ существует |
|||
единственная такая точка, что педальный треугольник этой точки |
|||
относительно данного треугольника ABC подобен треугольнику XYZ |
|||
при фиксированном порядке вершин. |
|
|
|
В доказательстве предыдущей теоремы мы получили два подоб- |
|||
ных треугольника и точку P внутри них, так что углы, образованные |
|||
сторонами и чевианами, связанными с точкой P, равны, но как бы |
|||
меняются местами (рис. 2.16). |
|
|
|
Таким образом, мы приходим к так называемому изогональному |
|||
сопряжению относительно треугольника. |
|
|
|
Пусть дан произвольный треугольник ABC и точка P, отличная от |
|||
вершин треугольника. Отразим прямые, соединяющие вершины тре- |
|||
угольника с точкой P, относительно биссектрис соответствующих уг- |
|||
лов треугольника. Оказывается, эти три прямые всегда пересекаются |
|||
в одной точке (или же параллельны, |
|
|
|
т. е. пересекаются в одной точке на про- |
|
|
B |
ективной плоскости), которую мы обо- |
|
|
|
значим P′ (рис. 2.18). Точку P′ назы- |
|
|
|
вают изогонально сопряженной точке P |
|
|
|
относительно треугольника ABC, а пре- |
|
P |
|
образование, переводящее каждую точ- |
|
P′ |
|
|
|
||
|
|
|
|
ку проективной плоскости в изогональ- |
|
|
|
но сопряженную, – изогональным сопря- |
A |
|
C |
жением. |
|
||
|
|
|
|
На самом деле корректность этого |
|
Рис. 2.18 |
|
определения мы почти доказали в лем- |
|
|
|
ме 2.1. Действительно, возьмем треугольник ABC и точку P. Пусть |
|||
A′B′C′ – окружностно-чевианный треугольник точки P относительно |
|||
треугольника ABC. Тогда треугольник ABC будет окружностно-че- |
|||
вианным треугольником точки P относительно треугольника A′B′C′, |
|||
а значит, подобен педальному треугольнику точки P относительно |
|||
A′B′C′. Следовательно, при подобии, переводящем педальный тре- |
|||
угольник точки P в треугольник ABC, точка P перейдет в точку P′, |
|||
которая как раз и будет изогонально сопряженной. |
|
|
|
Отметим несколько элементарных свойств изогонального сопря- |
|||
жения. |
|
|
|

§ 2.3. Некоторые факты из геометрии треугольника |
45 |
1. Если точка P не лежит на прямых, содержащих стороны треугольника, то точка P′ определяется однозначно и изогонально сопряженной точкой к P′ будет точка P. Такие две точки будем называть
изогонально сопряженными.
2.Изогонально сопряженной точкой к точке, лежащей на прямой, содержащей сторону треугольника, будет вершина треугольника, противоположная этой стороне.
3.Изогональное сопряжение оставляет на месте ровно 4 точки плоскости, а именно, центры вписанной и трех вневписанных окружностей треугольника.
4.Если точка P лежит на описанной окружности треугольника ABC, то изогонально сопряженной точке P будет точка на бесконечно удаленной прямой, которая задает направление, перпендикулярное прямой Симсона точки P относительно треугольника ABC (прямой, проходящей через проекции точки P на стороны треугольника ABC).
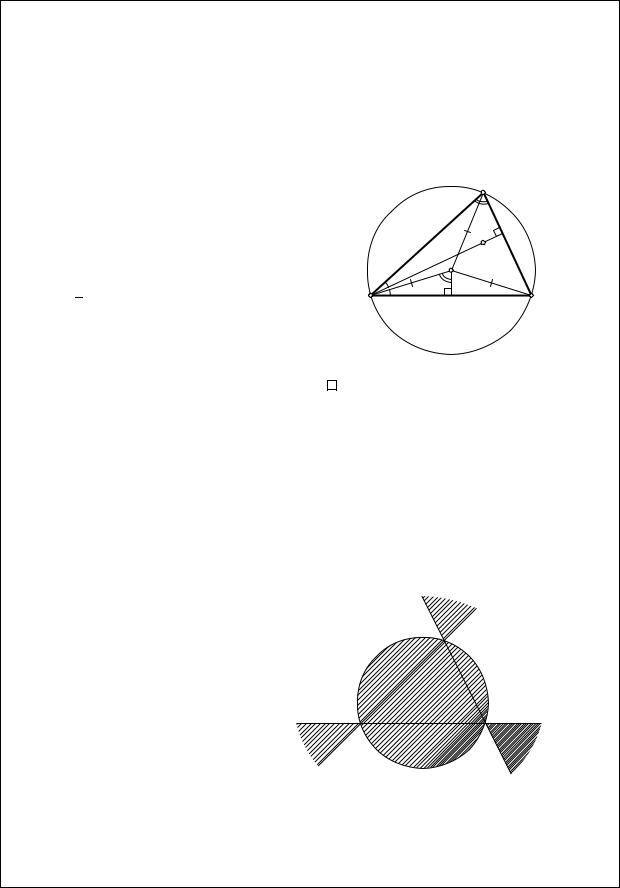
Первые три свойства очевидны. Докажем четвертое. Рассмотрим случай, изображен-
ный на рис. 2.19, остальные случаи разби- |
|
B |
||||||||||
|
|
|||||||||||
раются аналогично. Пусть точка P лежит на |
|
|
||||||||||
описанной окружности, а Pb и Pc – проекции |
|
X Pc |
||||||||||
точки P на стороны AC и AB соответственно. |
|
|
||||||||||
Точку пересечения прямой Симсона точки P |
|
Pb |
||||||||||
с прямой a, симметричной AP относитель- |
A |
|||||||||||
C |
||||||||||||
|
||||||||||||
но биссектрисы A, обозначим через X. Че- |
|
|
||||||||||
тырехугольник APPcPb вписанный, а значит, |
|
P |
||||||||||
|
|
|||||||||||
|
APb◦Pc |
= 180◦ |
− |
APP = 180◦ |
− |
(90◦ |
− |
PAP ) = |
|
|
||
|
|
|
◦c |
|
c |
|
|
|||||
= 90 + PAPc = 90 |
+ XAPb. Но, |
поскольку |
|
Рис. 2.19 |
||||||||
внешний угол равен сумме двух оставшихся |
|
|||||||||||
|
|
|||||||||||
внутренних углов треугольника, AXPb = 90◦. Аналогично доказыва- |
||||||||||||
ется, что прямые, симметричные PB и PC относительно биссектрис |
||||||||||||
соответствующих углов, перпендикулярны PbPc. |
|
|||||||||||
|
Из приведенного доказательства существования изогонально со- |
|||||||||||
пряженной точки сложно получить какие-нибудь его свойства. Мы |
||||||||||||
сейчас приведем еще один способ построения изогонально сопряжен- |
||||||||||||
ной точки, который сразу же выведет нас на несколько красивых |
||||||||||||
свойств этого преобразования. |
|
|
|
|
||||||||
|
Пусть точка P лежит внутри треугольника ABC, точка Pa симмет- |
|||||||||||
рична ей относительно стороны BC, точки Pb и Pc определены ана- |
||||||||||||
логично (рис. 2.20). Пусть P′ – это центр описанной окружности тре- |
||||||||||||
угольника PaPbPc. Точка C равноудалена от Pa и Pb, следовательно, |
||||||||||||
прямая CP′ является серединным перпендикуляром к отрезку PaPb. |
||||||||||||
А значит, PaCP′ = 21 PaCPb = C. Но тогда BCP′ = PaCP′ − BCPa = |
||||||||||||

46 Глава 2. Некоторые факты классической геометрии
B
Pc
 Pa
Pa
P′
P
A  C
C
Pb |
Рис. 2.20
= C − BCP = ACP. Аналогично показывается, что ABP′ = CBP и BAP′ = CAP. А это и означает, что точка P′ изогонально сопряжена P относительно ABC.
Если точка P лежит вне треугольника, то рассуждения абсолютно аналогичны, но, когда точка P лежит на описанной окружности треугольника ABC, треугольник PaPbPc вырожден. Тогда центр описанной окружности треугольника PaPbPc не определен (хотя естественно описанной окружностью считать прямую PaPb, а ее центром – точку на бесконечно удаленной прямой, соответствующую направлению, перпендикулярному PaPb).
Из второго построения изогонально сопряженных точек также следует, что центр педальной окружности точки P – это середина отрезка PP′, а радиус в два раза меньше длины отрезка P′Pa, поскольку педальная окружность точки P – это окружность, получающаяся из описанной окружности треугольника PaPbPc гомотетией с центром
в точке P и коэффициентом 12 .
Отсюда также следует такая теорема.
Теорема 2.8. Педальные окружности двух точек совпадают тогда и только тогда, когда они изогонально сопряжены.
Доказательство. Действительно, если точки P и P′ изогонально сопряжены, то их педальная окружность – это окружность с центром
в середине отрезка PP′ и радиусом |
P′Pa |
= |
PPa′ |
, где Pa и Pa′ |
– это точки, |
2 |
|
||||
|
2 |
|
|
||
симметричные P и P′ относительно стороны BC треугольника ABC. Докажем обратное. Если педальные окружности точек P и Q сов-
падают, то по доказанному выше они совпадают с педальной окружностью точки P′, изогонально сопряженной точке P. По принципу Дирихле у педального треугольника точки Q две из трех вершин общие с педальным треугольником либо точки P, либо точки P′. Следо-
§ 2.3. Некоторые факты из геометрии треугольника |
47 |
|
вательно, точка Q совпадает с одной из этих точек, потому что проек- |
||
ции точки на две прямые полностью задают положение этой точки. |
||
Непосредственно из этой теоремы следует, что ортоцентр H тре- |
||
угольника ABC изогонально сопряжен центру описанной окружно- |
||
сти O. Действительно, педальные окружности точек H и O совпадают |
||
с окружностью девяти точек Эйлера. |
|
|
Конечно, это можно доказать непосред- |
|
B |
|
|
|
ственно подсчетом углов. Рассмотрим |
|
|
случай, изображенный на рис. 2.21, |
|
|
остальные случаи разбираются анало- |
|
H |
гично. Мы имеем BAH = 90◦ − B, |
|
|
|
O |
|
но AOC = 2 B, следовательно, OAC = |
|
|
= 21 (180◦ −2 B) = 90◦ − B. Отсюда сле- |
A |
C |
дует, что BAH = OAC, а это и означа- |
|
|
ет, что AH при симметрии относитель- |
|
|
но биссектрисы угла A переходит в пря- |
|
|
мую AO. Для других двух углов доказа- |
|
Рис. 2.21 |
тельство аналогично. |
|
|
|
|
|
Пусть Ka, Kb и Kc – это точки пересечения прямых BC и P′Pa, |
||
AC и P′Pb, AB и P′Pc соответственно. Понятно, что PKaB = P′KaC. |
||
Следовательно, коника с фокусами в P и P′ и суммой расстояний до |
||
фокусов (или модулем разности в случае гиперболы), равной P′Pa, |
||
касается прямой BC. Аналогично показывается, что эта же коника |
||
касается двух других сторон треугольника, поскольку расстояния |
||
P′Pa = P′Pb = P′Pc равны удвоенному радиусу педальной окружности |
||
точки P. На рис. 2.22 заштрихованы зоны, где соответствующие точ- |
||
кам коники будут гиперболами, и не заштрихованы области, где эти |
||
коники будут эллипсами. Точкам описанной окружности соответ- |
||
ствуют параболы. |
|
|
|
Рис. 2.22 |
|

48 Глава 2. Некоторые факты классической геометрии
Если точки P и Q изогонально сопряжены в многоугольнике (т. е. для любой вершины X этого многоугольника прямые XP и XQ симметричны относительно биссектрисы угла X), то найдется коника, касающаяся всех сторон многоугольника, с фокусами в этих точках. Обратное тоже верно, т. е. если коника вписана в многоугольник, то ее фокусы изогонально сопряжены относительно этого многоугольника. Аналогично можно показать, что тогда педальные окружности точек P и Q совпадают (помимо того что они существуют!).
В следующем параграфе будет показано, что для любых пяти прямых существует единственная касающаяся их коника. Поэтому для пятиугольника существует только одна пара изогонально сопряженных точек. Для четырехугольника, как легко понять, такие точки образуют некоторую кривую (на самом деле она будет кубикой – кривой третьего порядка), а для шестиугольников (и многоугольников
сбольшим числом сторон) таких точек, как правило, не существует.
Спомощью изогонального сопряжения можно довольно просто доказать теорему Паскаля, причем в общем виде.
Теорема 2.9 (Паскаль). Пусть точки A, B, C, D, E и F лежат на |
||||
конике. Тогда точки пересечения прямых AB и DE, BC и EF, CD и FA |
||||
лежат на одной прямой. |
|
|
|
|
Доказательство. Мы рассмотрим только один случай расположе- |
||||
ния точек на окружности (конике). Остальные рассматриваются ана- |
||||
логично. |
|
|
|
|
Переведем проективным преобразовани- |
|
|
B |
|
ем конику в окружность. Получим следую- |
|
|
|
|
|
|
|
|
|
щую конструкцию (рис. 2.23). |
D |
|
|
F |
|
|
|
|
|
Точки A, B, C, D, E и F лежат на од- |
|
|
|
|
ной окружности. Пусть прямые AB и DE |
|
X |
|
|
пересекаются в точке X, прямые BC и EF – |
|
|
Y |
|
|
|
Z |
||
в точке Y, а AF и CD – в точке Z. Надо до- |
|
|
|
|
|
|
|
|
|
казать, что точки X, Y и Z лежат на одной |
|
|
|
|
прямой. |
|
|
|
C |
Углы BAF и BCF равны, поскольку опи- |
A |
|
|
|
раются на одну дугу. Аналогично равны |
|
|
E |
|
углы CDE и CFE. Кроме того, треугольники |
|
|
|
|
|
|
|
|
|
AZD и CZF подобны. Рассмотрим преобра- |
|
|
Рис. 2.23 |
|
зование подобия, переводящее треугольник |
|
|
|
|
AZD в треугольник CZF. При этом преобразовании точка X перей- |
||||
дет в точку X′, изогонально сопряженную точке Y относительно тре- |
||||
угольника CZF (в силу вышеуказанных равенств углов). Следователь- |
||||
но, AZX = CZX′ = FZY, а это и означает, что точки X, Z и Y лежат |
||||
на одной прямой. |
|
|
|
|
Приведем еще несколько пар изогонально сопряженных точек. |
||||
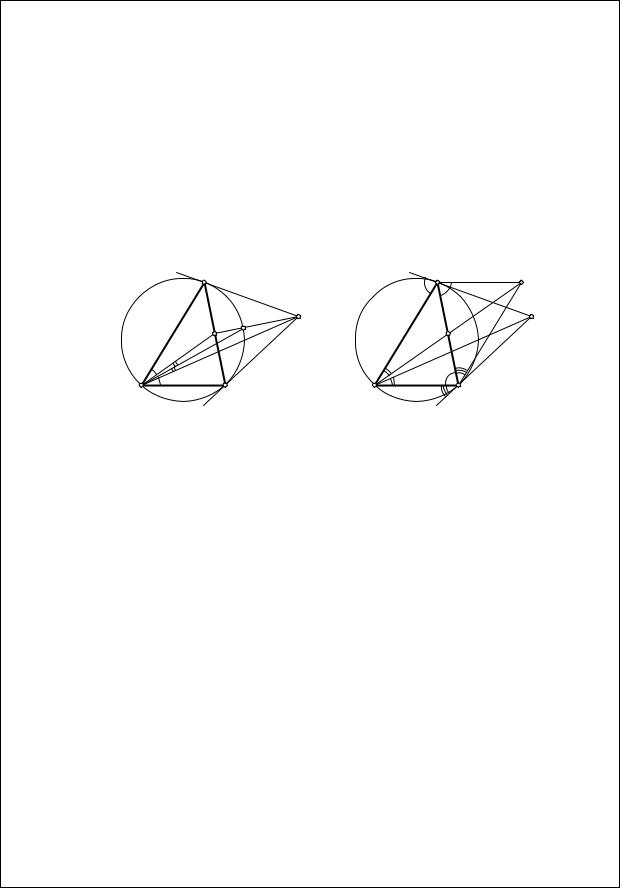
§ 2.3. Некоторые факты из геометрии треугольника |
49 |
1. Центр тяжести – точка Лемуана
Прямые, симметричные медианам относительно биссектрис соответствующих углов, называются симедианами. Точка пересечения симедиан, очевидно, изогонально сопряжена точке пересечения медиан. Эту точку называют точкой Лемуана.
Отметим несколько основных свойств точки Лемуана, которые в чем-то похожи на свойства центра тяжести.
1а. Пусть касательные к описанной окружности треугольника ABC, проведенные в точках B и C, пересекаются в точке A1. Тогда AA1 – симедиана треугольника ABC (рис. 2.24).
B |
|
B |
|
|
|
|
A ′ |
Ma |
A 1 |
Ma |
A 1 |
A |
C |
A |
C |
Рис. 2.24 Рис. 2.25
Действительно, пусть точка Ma – середина стороны BC, тогда она инверсна точке A1 относительно описанной окружности треугольника ABC. Значит, основание биссектрисы угла MaAA1 совпадает с серединой дуги BC, т. е. эта биссектриса совпадает с биссектрисой угла BAC. Ну а тогда прямая AA1 симметрична медиане AMa относительно биссектрисы угла A.
Другое изящное доказательство этого факта основано исключительно на существовании изогонального сопряжения. Мы просто укажем точку, изогонально сопряженную A1. Это точка, симметричная точке A относительно Ma; она, очевидно, лежит на медиане AMa (обозначим ее через A′; см. рис. 2.25). Как нетрудно проверить, прямые BA′ и CA′ при отражении относительно биссектрис соответствующих углов переходят в касательные к описанной окружности. Ну а значит, A′ переходит в A1.
Из этой теоремы следует, что симедиану можно построить с помощью линейки, если дана описанная окружность треугольника. При проективных преобразованиях, оставляющих описанную окружность треугольника ABC на месте, симедианы переходят в симедианы и точка Лемуана – в точку Лемуана. Это свойство в некотором смысле аналогично тому, что при аффинных преобразования центр тяжести треугольника переходит в центр тяжести.

50 Глава 2. Некоторые факты классической геометрии |
|||
Как следствие, стоит также отметить, что точка Лемуана будет |
|||
точкой Жергонна (см. ниже) треугольника A1B1C1, где точки B1 и C1 |
|||
строятся аналогично точке A1. |
|
|
|
1б. Симедиана делит сторону в отношении, равном отношению |
|||
квадратов прилегающих сторон. |
|
|
|
Обозначим точку пересечения симедианы угла A со стороной BC |
|||
через La, а середину отрезка BC через Ma. |
|
|
|
Поскольку площади треугольников ABMa и ACMa равны, отноше- |
|||
ние расстояний от точки Ma до сторон AB и AC обратно пропорцио- |
|||
нально отношению этих сторон. Но поскольку прямая ALa симмет- |
|||
рична прямой AMa относительно биссектрисы угла A, произведение |
|||
отношений расстояний от Ma и La до AB и AC равно 1. Следовательно, |
|||
отношение расстояний от La до AB и AC равно отношению длин этих |
|||
сторон, а значит, площади треугольников ABLa и ACLa относятся как |
|||
квадраты длин сторон AB и AC. Но, с другой стороны, это отношение |
|||
равно отношению BLa и CLa, поскольку у этих треугольников общая |
|||
высота. |
|
|
|
1в. Сумма квадратов расстояний от точки P до вершин тре- |
|||
угольника достигает своего минимума, когда точка P – это точка |
|||
пересечения медиан. В то же время сумма квадратов расстояний до |
|||
сторон достигает своего минимума в точке Лемуана. |
|||
Этот факт нетрудно вывести из предыдущего. |
|||
2. Точки Брокара |
|
|
|
Оказывается, в любом треугольнике |
|
B |
|
ABC существует такая точка Br1, что |
|
|
|
BABr1 = CBBr1 = ACBr1. Если взять |
|
|
|
изогонально сопряженную к Br1 точку |
|
|
|
Br2, то, очевидно, ABBr2 = BCBr2 = |
|
Br2 |
|
|
|
||
= CABr2 (рис. 2.26). |
|
Br1 |
|
Эти две точки называют соответ- |
|
||
|
|
||
ственно первой и второй точками Бро- |
|
|
|
кара, а эллипс, касающийся сторон тре- |
A |
C |
|
угольника, с фокусами в этих точках |
|||
|
|
||
называют эллипсом Брокара. В пра- |
|
Рис. 2.26 |
|
вильном треугольнике эти две точки |
|
|
|
совпадают с центром треугольника, а эллипс – с вписанной окруж- |
|||
ностью. |
|
|
|
Докажем существование точки Br1. На сторонах треугольника по- |
|||
строим подобные ему треугольники BCA1, B1CA, BC1A так, как пока- |
|||
зано на рис. 2.27. |
|
|
|
Тогда описанные окружности этих треугольников (обозначим их |
|||
через wa, wb и wc) пересекаются в одной точке. Действительно, пусть |
|||
Br1 – это точка пересечения окружностей wa |
и wb , отличная от C. |
||
