Zaslavky-Akopyan

Упражнение 1. Докажите,

что сумма

Y

расстояний от любой точки внутри эллипса

X

до фокусов меньше, а от точки вне эллипса

больше длины большой оси.

F1

F2

Решение. Обозначим фокусы эллипса че-

рез F1 и F2, а точку через X. Точку пересече-

ния луча F1X с эллипсом обозначим через Y.

Пусть сначала точка X лежит внутри эллип-

Рис. 1.2

са. По неравенству треугольника F2X < XY +

+ YF2, а значит, F1X + XF2 < F1X + XY + YF2 = F1Y + F2Y (рис. 1.2).

Но F1Y + F2Y равно длине веревки, к которой привязана коза,

т. е. большой оси эллипса. Рассуждая аналогично в случае, если точ-

ка X лежит вне эллипса, получаем F2Y < XY + XF2. Следовательно,

F1X + XF2 = F1Y + YX + XF2 > F1Y + F2Y.

Эллипсы часто встречаются в механике. Так, например, планета,

двигаясь вокруг Солнца, описывает эллипс, причем Солнце находит-

ся в одном из его фокусов (закон Кеплера).

Эллипс является одним из примеров кривых второго порядка, или

коник. Другими примерами таких кривых являются парабола и ги-

пербола.

Гиперболой называется множество точек, модуль разности рассто-

яний от которых до двух фиксированных точек, называемых фокуса-

ми, постоянен.

Гипербола состоит из двух дуг, которые сколь угодно близко при-

ближаются к двум прямым, называемым асимптотами гиперболы

(рис. 1.3). Гипербола с перпендикулярными асимптотами называется

равносторонней.

Прямая, проходящая через фокусы гиперболы, является ее осью

симметрии и называется действительной осью. Перпендикулярная

ей прямая, проходящая через середину

отрезка между фокусами, также являет-

b

ся осью симметрии и называется мнимой

осью гиперболы.

Если комета летит мимо Солнца и си-

лы притяжения Солнца недостаточно, что-

F1

a

бы оставить комету в пределах солнечной

F2

системы, то траекторией кометы будет ду-

l1

l2

га гиперболы, фокус которой находится

в центре Солнца.

Параболой называется множество то-

Рис. 1.3. F1 и F2 – фокусы,

чек, расстояния от которых до фиксиро-

a и b – действительная и

ванных точки и прямой равны. Эти точ-

мнимая оси,

ка и прямая называются фокусом и ди-

l1 и l2 – асимптоты

§ 1.1. Определения

9

ректрисой параболы соответственно. Прямая, перпендикулярная ди-

ректрисе и проходящая через фокус, называется осью параболы

(рис. 1.4). Очевидно, что эта прямая является

осью симметрии параболы.

l′

Например, камень, брошенный под углом

к горизонту, летит по параболе.

В каком-то смысле, с геометрической точ-

F

ки зрения, парабола всего одна (как и окруж-

ность). Точнее говоря, все параболы подобны,

l

т. е. они переводятся друг в друга поворотной

гомотетией.

Рис. 1.4. F – фокус,

Рассмотрим семейство эллипсов с фоку-

l и l′ – директриса и ось

сом в фиксированной точке и проходящих

параболы

через заданную точку. Второй же фокус

устремим к бесконечности вдоль какого-то

Z′

X

направления. Тогда эти эллипсы будут стре-

F

миться к параболе с тем же фокусом и осью,

X ′

параллельной направлению, вдоль которого

Z

мы уводили второй фокус. Аналогичный экс-

Y′

Y

перимент можно повторить и для гипербол.

Таким образом, парабола является предель-

Рис. 1.5

ным случаем как эллипса, так и гиперболы.

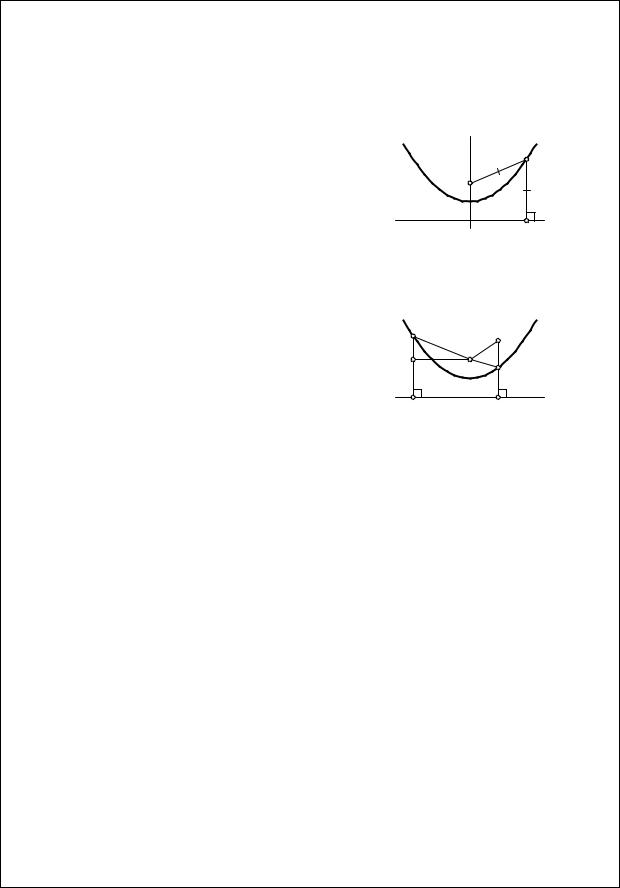
Упражнение 2. Сформулируйте и докажите для параболы и ги-

перболы утверждения, аналогичные утверждению из упражнения 1.

Решение. Для точек внутри параболы расстояние до фокуса мень-

ше, чем расстояние до директрисы, а для точек вне параболы наобо-

рот (рис. 1.5).

Проекцию точки X на директрису обозначим через Y, а точку

пересечения XY с параболой через Z. Через F обозначим фокус па-

раболы. По определению параболы FZ = ZY. Если точка X лежит

внутри параболы, то XY = XZ + ZY. По неравенству треугольника

FX < FZ + ZX = ZY + ZX = XY. Если точка X и парабола лежат по раз-

ные стороны от директрисы, то утверждение очевидно. Пусть точка

X лежит вне параболы, но по ту же сторону от директрисы, тогда

ZY = ZX + XY, и по неравенству треугольника FX + XZ > FZ = ZY =

10 Глава 1. Элементарные свойства кривых второго порядка

F2X = F2Y + YX. По неравенству треуголь-

ника F1X < F1Y + YX, значит, F2X − F1X >

X

Y

> (F2Y + YX) − (F1Y + YX) = F2Y − F1Y = d.

Если же точка X лежит вне Г, то, взяв за

точку Y пересечение F1X и Г, получим F1X =

F1

F2

= F1Y + YX. По неравенству треугольника

Y′

F2X < F2Y + YX. Следовательно, F2X − F1X <

< (F2Y + YX) − (F1Y + YX) = F2Y − F1Y = d.

ˆ

X ′

Отметим (пока без доказательства), что

и эллипс, и парабола, и гипербола обладают

Рис. 1.6

следующими свойствами: любая прямая пе-

ресекает каждую из этих кривых не более чем в двух точках, и из

любой точки плоскости к кривой можно провести не более двух каса-

тельных. Эти свойства являются очевидными следствиями результа-

тов § 1.5.