
Одобрена Ученым советом метеорологического
и океанологического факультетов
УДК 532
Методические указания по дисциплине Механика жидкости и газа»,
для высших учебных заведений, часть I «Гидромеханика» - СПб.:
изд. РГГМУ, 2004. - 32 с.
Составитель: В.В. Петрова, канд. физ.-мат. наук, ст. преподаватель РГГМУ
Рецензент: М.А. Рыдалевская, проф. СПбГУ
Ответственный редактор: В. А. Федотов, канд. физ.-мат. наук, доц. РГГМУ
© В.В. Петрова, 2004
о Российский государственный гидрометеорологический университет (РГГМУ), 2004
ПРЕДИСЛОВИЕ
Механика жидкости или гидромеханика - это наука, которая изучает движение жидких и газообразных сред и их взаимодействие с обтекаемыми телами. При рассмотрении сред обычно используют модель сплошной среды, т.е. считается, что жидкость или газ заполняет пространство без промежутков непрерывным образом. Каждой точке этого пространства можно поставить в соответствие ряд параметров (скорость движения, плотность, температуру, давление и т.д.).
Изучению гидромеханики предшествует изучение математики, в особенности векторной алгебры и математического анализа, а также физики, где следует обратить особое внимание на основные законы сохранения. Сама гидромеханика является основой для динамической метеорологии, динамики океана, теории климата и других специальных дисциплин.
Студент должен знать теоретические основы дисциплины, уметь решать задачи гидромеханики и проводить физическое обоснование своего решения.
Литература
Кочин Н.Е. Векторное исчисление и начала тензорного исчисления - М: Наука,
1965,426 с.
Кочин Н.Е.., Кибель И.Я., Розе Н.В. Теоретическая гидромеханика - М: ГИМФЛ,
1963, ч. 1,583 с.
Палагин ЭТ.. Славин И. А. Основы гидромеханики - Л: ЛГМИ, 1974, 244 с.
Лойцянский Л.Г. Механика жидкости и газа - М: Наука, 1987, 840 с.
Седов Л.И. Механика сплошной среды - М: Наука, 1970, Т. 1, 492 с.
Программа дисциплины «Механика жидкости и газа» для высших учебных заведений - СПб.: Изд. РГГМУ, 2002 - 9с.
Введение
В гидромеханике приходится иметь дело с величинами различной природы. Наиболее простым из них является скаляр - это просто число, соотнесенное определенной точке пространства. Скалярная величина не меняет своего значения при переходе от одной системы координат к другой.
Вектором
называется расположенный в пространстве
направленный отрезок. Численное
значение вектора называется модулем и
равно его длине. Для определения вектора
достаточно задать три его проекции
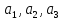 ,
на координатные оси. При переходе от
одной системы координат (х, у,z)
или
(
,
на координатные оси. При переходе от
одной системы координат (х, у,z)
или
( )
к другой системе координат
)
к другой системе координат
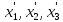 проекции
вектораа
на новые координатные оси изменят свое
значение. Обозначим новые координаты
проекции
вектораа
на новые координатные оси изменят свое
значение. Обозначим новые координаты
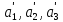 .
Как известно, при изменении системы
координат может быть выписана таблица
направляющих косинусов
.
Как известно, при изменении системы
координат может быть выписана таблица
направляющих косинусов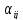 между новыми и старыми координатами.
Компоненты вектора преобразуются по
следующим формулам
между новыми и старыми координатами.
Компоненты вектора преобразуются по
следующим формулам
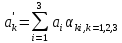
Вектора можно складывать, вычитать и перемножать согласно правилам векторной алгебры.
Векторное поле определяется векторной функцией точки, т. е. это вектор, каждая компонента которого является функцией от координат. В координатной форме

Тензор второго ранга характеризуется таблицей из девяти величин

компоненты
 которой
при переходе от системы координат(
которой
при переходе от системы координат(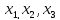 )к
системе
)к
системе
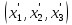 преобразуются
по формулам
преобразуются
по формулам

В гидромеханике также приходится исследовать изменение различных параметров в зависимости от координат. В связи с этим вводятся в рассмотрение следующие дифференциальные операторы.
Градиент. Этот оператор применяется к скалярной функции и (х, у, z), дает в результате векторную функцию

В каждой точке вектор градиента направлен по нормали к поверхности, определяемой функцией и (х, у, z), в сторону ее возрастания.
Дивергенция.
Дивергенцией векторного поля называется скалярная величина,
определяемая по формуле
называется скалярная величина,
определяемая по формуле

Ротор.
Этот оператор применяется к векторному
полю
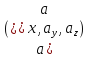 и дает в результате векторное поле
и дает в результате векторное поле
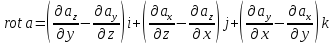
Многие из приведенных операторов и векторов широко применяются в кинематике жидкости.
Литература
[1] с. 5-59, с. 101-164.
[4] с. 9-30.
[5] с. 9- 15.
Кинематика жидкой среды
Общей
задачей кинематики является описание
движения среды безотносительно к
причинам, вызвавшим это движение.
Вследствие этого кинематика изучает
главным образом свойства векторного
поля скоростей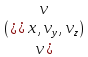 .
Мы
будем рассматривать случай плоского
движения, т. е. считаем, что
.
Мы
будем рассматривать случай плоского
движения, т. е. считаем, что

где х, у - координаты точки, t - время.
Траекторией частицы называется геометрическое место точек, через которые движущаяся частица последовательно переходит во времени. Поскольку траектория характеризует скорость одной частицы в разные моменты времени, она определяется следующей системой уравнений:
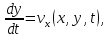
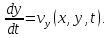
(1)
Интегрируя и решая систему дифференциальных уравнений (1), мы получим бесчисленное множество решений. Для определения произвольных постоянных должны быть дополнительно заданы условия

(2)
В
таком случае мы получим траекторию,
проходящую в момент
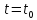 через
точку
через
точку .
.
Линией
тока
называется линия, у которой в данный
момент времени в любой точке вектор
скорости направлен по касательной к
ней. Таким образом, линия тока определяет
направление скоростей разных точек
среды в один момент времени
 .
Уравнение
для определения линий тока запишется
следующим образом
.
Уравнение
для определения линий тока запишется
следующим образом
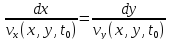
(3)
Уравнение
(3) также дает бесчисленное множество
решений, поэтому для нахождения
конкретной линии тока следует задать
точку
 ,
через которую она проходит в момент
времени
,
через которую она проходит в момент
времени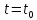 .
.
В
общем случае траектории и линии тока
не совпадают. Совпадают они только
при стационарном
течении, когда
 не
зависят от времени.
не
зависят от времени.
Если мы выделим в жидкости некоторый малый объем и рассмотрим его движение, то с течением времени этот объем, очевидно, будет деформироваться. Для численной характеристики этой деформации вводится так называемый тензор скоростей деформации, представляющий собой следующую таблицу
(4)
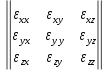 ,
,
где
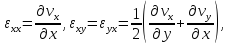
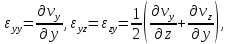
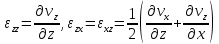 .
.
(5)
Физический
смысл диагональных компонент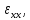
 состоит в том, что они определяют
скорость растяжения (или сжатия) объема
жидкости вдоль осей х, у,z.
Остальные,
недиагональные компоненты характеризуют
скорость скашивания объема, которое
будет происходить при движении. Поскольку
мы рассматриваем плоское движение,
элементы
состоит в том, что они определяют
скорость растяжения (или сжатия) объема
жидкости вдоль осей х, у,z.
Остальные,
недиагональные компоненты характеризуют
скорость скашивания объема, которое
будет происходить при движении. Поскольку
мы рассматриваем плоское движение,
элементы
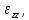
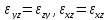 будут
равны нулю.
будут
равны нулю.
При движении объем жидкости может не только деформироваться, но и расширяться (или сжиматься). Это явление численно характеризуется скоростью объемного расширения жидкости
 .
.
(6)
В случае, когда I=0, жидкость называется несжимаемой.
В гидромеханике вводится также величина, характеризующая вихревое движение точек среды. Это так называемый вектор вихря скорости.
 =
rot
v.
=
rot
v.
(7)
Если
в пространстве существует область, где
 0,
то в этой области течение называетсябезвихревым.
0,
то в этой области течение называетсябезвихревым.
Иногда в задачах требуется вычислить полные производные по времени от гидродинамических величин (от скорости, температуры, давления и т.п.). Гидродинамические величины зависят от времени и координат, а координаты могут также зависеть от времени, если жидкая частица перемещается. Следовательно, согласно формулам математического анализа, можем записать для полной производной по времени от гидродинамического параметра A(x,y,t) следующее выражение

В частности, если А = v, то мы получим формулу для вычисления ускорения

(8)
Или в проекциях
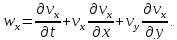
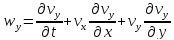
(9)
Таким образом, мы можем вычислить ускорения любой точки среды в любой момент времени.
В
случае безвихревого течения (когда rot
v
=
0) вводится понятие потенциала скорости
- функция
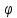 (x,y,t).
По определению
(x,y,t).
По определению
v
=
grad

т. е.
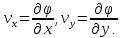
(10)
Если же нам известно поле скоростей, а нужно найти потенциал в некоторой точке, то необходимо вычислить криволинейный интеграл по произвольному контуру, соединяющему точку А - начало отсчета потенциала и точку В, в которой ищется потенциал.

Для
плоского движения несжимаемой жидкости
(когда div
v
=
0) вводят функцию тока
 (х,
у). По определению
(х,
у). По определению
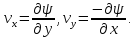
(11)
Аналогично формуле для потенциала

(12)
Функция
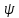 (x,
у)
называется функцией тока, т. к. на каждой
линии тока она сохраняет постоянное
значение. Это свойство позволяет
проводить исследование линий тока,
когда их трудно найти непосредственно.
(x,
у)
называется функцией тока, т. к. на каждой
линии тока она сохраняет постоянное
значение. Это свойство позволяет
проводить исследование линий тока,
когда их трудно найти непосредственно.
Остановимся на решении характерных задач по кинематике жидкости.
Задача
1. Для плоского поля скоростей v(4t
+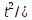 2,-
х) определить
2,-
х) определить
1) линию тока и траекторию, проходящие через точку A(0,1/16) в момент времени t = 0 ;
2) тензор скоростей деформации и сжимаемость среды;
3) поле вихря;
4) ускорение точек среды.
Решение. 1). Траекторию, согласно формуле (1), мы определяем из системы уравнений
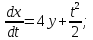
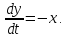
Продифференцируем второе уравнение системы еще раз по t. Получим
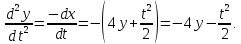
или
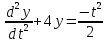
Это
линейное неоднородное уравнение второго
порядка с постоянными коэффициентами.
Его решение складывается из общего
решения однородного уравнения
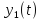 и частного решения неоднородного
уравнения
и частного решения неоднородного
уравнения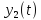 .
Решение
.
Решение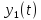 находится
путем отыскания корней характеристического
уравнения.
находится
путем отыскания корней характеристического
уравнения.
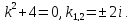
Следовательно,
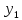 (t)
=
(t)
=
 cos
2t
+
cos
2t
+
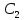 sin
2t.
sin
2t.
Используя
метод неопределенных коэффициентов,
по виду неоднородной правой части
заключаем, что решение
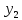 (t)
.нужно искать в виде
(t)
.нужно искать в виде
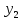 (t)
= а
(t)
= а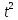 +bt
+ c.
+bt
+ c.
Вычисляя
d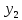 /dt
и
/dt
и
 /d
/d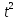 ,
подставляем
вторую производную в исходное
неоднородное уравнение. Получим
,
подставляем
вторую производную в исходное
неоднородное уравнение. Получим
2a+
4(а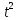 +bt
+ с) = -
+bt
+ с) = -
Приравнивая коэффициенты при одинаковых степенях t, имеем
4я = -1/2, 4b = 0, 2а + 4с = 0,
откуда
а = -1/8, b = 0, с = 1/16.

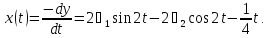
Определим теперь произвольные постоянные. По условию
x(0) = 0, у(0) = 1/16,
откуда
находим, что
 =
=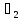 = 0. Уравнение траектории, таким образом,
имеет вид
= 0. Уравнение траектории, таким образом,
имеет вид
x(t)
= -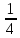 t,
y(t)
= -
t,
y(t)
= -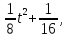
или
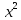 =-1/2
(у-1/16).
=-1/2
(у-1/16).
Это уравнение параболы.
Для определения линий тока воспользуемся формулой (3). В нашем случае можем записать
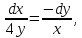
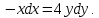
Разделив таким образом переменные и интегрируя, получим
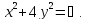
Подставляя начальные значения, найдем С = 1/64. Уравнение линии тока примет вид уравнения эллипса
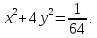
Рис. 1 иллюстрирует полученные выражения для траектории и линии тока.
|
|
у |
|
|
|
|
|
\ -J \ |
|
\ |
\ |
Рис.1.
2) Компоненты тензора скоростей деформации находятся по формуле (5). Проведя вычисления, определим, что почти все элементы тензора равны нулю, за исключением двух.
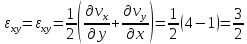
Сжимаемость среды I в данном случае также нулевая.
3) Поле вихря находится по формуле (7) и с помощью определения ротора.
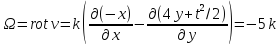
4) Для определения ускорения воспользуемся формулами (9).
Получим
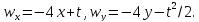
Задача
2. По известному потенциалу скорости
 (х,у)
=
(х,у)
= найти функцию тока
найти функцию тока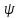 (х,
у).
(х,
у).
Решение. Прежде всего, проверим, выполнено ли условие несжимаемости среды
div v = 0, т.к. только в этом случае возможно существование функции тока.
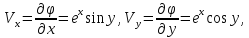
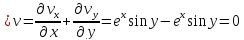
Рис.2.
Найдем
функцию тока на основе формулы (12), где
начальную точку отсчета А выберем в
начале координат. Пусть точка В имеет
координаты ( ).
Т. к. мы имеем право интегрировать по
произвольному пути, выберем в качестве
контура ломаную АСВ (см. рис. 2). Очевидно,
).
Т. к. мы имеем право интегрировать по
произвольному пути, выберем в качестве
контура ломаную АСВ (см. рис. 2). Очевидно,
на
AС:у=0,
0 x
x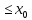 ,
d
у
=0,
,
d
у
=0,
на
СВ: х =
 ,d
х
= 0.
,d
х
= 0.
Подставляя это в формулу (12), получим


Литература
[2] с. 9-12,. с. 16-21, с. 31 -35,
[3] с. 14-80,
[41 с. 31 - 53,
[5] с. 22 - 108.
