
Лекция 10
.pdf1
Проф. Власов А.Н. Материалы лекций по курсу «ОБЩАЯ ФИЗИКА» 2015
1-й семестр
Лекция № 10
Тема лекции:
Термодинамика
План:
1.Термодинамическая система. Принцип детального равновесия ….………… 1
2.Первый закон термодинамики……………………………………………..……6
3.Графическое изображение термодинамических процессов…………...…….9
4.Теплоѐмкость вещества……………………………………………..…….…….12
5.Изохорный процесс…………………………………………………………..…13
6.Изобарный процесс……………………………………………………………..15
7.Изотермный процесс……………………………………………………………17
8.Адиабатный процесс…………………………………………………………….18
9.Политропный процесс…………………………………………………………..20
1.Термодинамическая система. Принцип детального равновесия.
Втермодинамике не интересуются движением частиц и не используются модельные представления о строении веществ, а ограничиваются лишь установлением связей между непосредственно измеряемыми в опытах величинами (объѐмом V , давлением P , температурой T и т.д.). Значения макрохарактеристик и их изменения находятся в термодинамике дедуктивным методом с помощью общих основополагающих принципов (начал).
Основными понятиями термодинамики являются понятия: термодинамическая система, термодинамическое состояние, термодинамический процесс.
1
2
Под термодинамической системой понимается совокупность макроскопических тел любой физикохимической природы, между которыми возможен теплообмен. Тела, не входящие в систему, называются внешними.
Термодинамическая система считается изолированной, если она не взаимодействует с внешними телами, и неизолированной — в противоположном случае. Понятие «изолированная» система — одна из важнейших абстракций термодинамики. Реальные макросистемы можно считать изолированными лишь в некотором приближении.
Свойства макроскопической системы в целом описываются совокупностью макроскопических физических величин, называемых термодинамическими параметрами. Различают внешние параметры, определяемые положением и свойствами внешних тел и полей (объем системы V, напряженность электрического поля Е и т. д.), и внутренние параметры, определяемые свойствами и поведением частиц самой системы (давление внутри системы Р, поляризация среды и т. д.).
Каждой совокупности термодинамических параметров соответствует определенное макроскопическое состояние системы. Обычно вводят минимальное число термодинамических параметров, полностью описывающих состояние системы. Это число аналогично числу степеней свободы в механике. Так для идеального газа массой т достаточно ввести два макропараметра — давление и объем. Другие параметры (температура, плотность и т. д.) будут функциями выбранных двух.
2
3
Параметры, не зависящие от способа перевода системы в рассматриваемое состояние, называются функциями состояния. К таким функциям относится, например, внутренняя энергия системы.
Функции состояния имеют для термодинамики особо важное значение.
Состояние системы называется стационарным, если параметры системы с течением времени не изменяются, и нестационарным — в противоположном случае.
Стационарное состояние может быть неравновесным, если неизменность параметров поддерживается какимилибо внешними воздействиями и равновесным, если все параметры системы неизменны и эта неизменность поддерживается в системе самопроизвольно.
В термодинамике постулируется, что изолированные системы с течением времени неизбежно и самопроизвольно переходят в равновесное состояние (состояние теплового равновесия) и никогда из него самопроизвольно выйти не могут.
Макроскопические параметры, характеризующие равновесное состояние системы, не являются независимыми. Закон, выражающий зависимость между параметрами термодинамической системы в условиях равновесия, называется уравнением состояния.
Всякое изменение в термодинамической системе,
связанное с изменением хотя бы одного из ее макропара-
метров, называется термодинамическим процессом.
В результате термодинамического процесса система переходит из одного макросостояния в другое.
3
4
Подходящим воздействием систему можно вернуть обратно в исходное состояние. Второй процесс по отношению к первому (прямому) называют обратным. Вместе прямой и обратный процесс называют круговым или циклическим.
В результате циклического процесса система возвращается в исходное состояние. Процесс называется равновесным или статическим, если любое промежуточное состояние системы является равновесным. Следовательно, равновесный термодинамический процесс состоит из бесконечно близких равновесных состояний, последовательно сменяющих друг друга. Понятие «равновесный процесс» — одна из важнейших абстракций термодинамики. Реальные процессы в макросистемах можно приближенно считать равновесными.
Введем понятие обратимого процесса.
Термодинамический процесс, совершаемый системой, называется обратимым, если после него можно возвратить систему и все взаимодействовавшие с ней тела в их начальные состояния таким образом, чтобы в других телах не возникло каких-либо остаточных изменений.
Процесс, который не удовлетворяет вышеуказанному условию, называется необратимым процессом.
Примером обратимого процесса могут служить незатухающие колебания, совершаемые телом в вакууме на абсолютно упругой пружине.
Примером необратимого процесса является торможение тела под действием силы трения. Если эта сила — единственная, действующая на тело, то скорость тела уменьшается и оно, в конце концов, останавливается. При
4
5
этом энергия механического движения тела как целого уменьшается и расходуется на увеличение энергии теплового движения частиц тела и окружающей среды.
Рассмотренный прямой процесс протекает самопроизвольно: он осуществляется без каких-либо процессов, происходящих с окружающими телами. Для осуществления обратного процесса возвращения системы в исходное состояние необходимо, чтобы остановившееся тело вновь пришло в движение за счет энергии, выделившейся при охлаждении его самого и окружающей среды.
Все процессы, сопровождающиеся трением, являются необратимыми.
Необходимое условие обратимости термодинамического процесса – его равновесность, т.е. когда явлениями переноса можно пренебречь.
В изучаемой здесь термодинамике равновесных систем, а также в молекулярной физике справедлив
принцип детального равновесия: «Любой
микроскопический процесс в равновесной системе должен протекать с такой же скоростью, что и обратный ему».
Воткрытых системах это принцип может нарушаться,
ав неравновесных системах этот принцип вовсе не соблюдается.
5
6
2. Первый закон термодинамики
Первый закон термодинамики формулируется следующим образом:
«Теплота, сообщаемая системе, расходуется на изменение внутренней энергии системы и на совершение системой работы против внешних сил».
Математически первый закон термодинамики представлен следующим соотношением:
|
Q U A , |
|
(1) |
где |
Q – теплота, сообщаемая системе, U |
– изменение |
|
внутренней энергии системы, A – |
работа, |
совершаемая |
|
системой против внешних сил. |
|
|
|
|
Если система представляет собой периодически |
||
действующую машину, в которой |
газ, пар |
или другое |
|
рабочее тело в результате совершения кругового процесса возвращается в исходное состояние, то U 0 и A Q .
Следовательно, нельзя построить периодически действующий двигатель, который совершал бы работу, большую подводимой к нему извне энергии (вечный двигатель первого рода невозможен).
Первый закон термодинамики обычно записывают для изменения состояния системы, вызванного сообщением ей малой теплоты Q , совершением системой элементарной
(малой) работы A |
и приводящего к малому изменению |
|
dU внутренней энергии. С учѐтом (1) имеем: |
|
|
|
Q dU A . |
(2) |
6
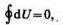
7
Отличия в записи
(
Q,
dU,
A
)
малых величин
теплоты и работы и изменения внутренней энергии имеют отнюдь не формальный характер, а выражают глубокие физические различия этих величин. Дело в том, что, внутренняя энергия системы является однозначной функцией ее состояния. Отсюда следует, что при совершении системой произвольного процесса, в результате которого она вновь возвращается в исходное состояние, полное изменение внутренней энергии системы равно нулю. Математической записью этого вывода служит тождество
(3)
которое является необходимым и достаточным условием для того, чтобы выражение dU представляло собой полный дифференциал. Как будет видно из дальнейшего, ни работа, ни теплота не являются функциями состояния и
поэтому |
Q |
и |
A |
не являются полными |
дифференциалами. |
|
|
|
|
Если к системе подводится теплота, то
Q
0
, если
отводится, то |
Q 0 |
. Общее количество теплоты, |
сообщаемое системе на участке 1-2, составляет
Q1 2
2 Q
1
.
Если система совершает работу над внешними
телами, то |
считается, что |
A 0 |
, если |
над системой |
совершают |
работу, то A 0 . |
Работа, |
совершаемая |
|
системой на участке 1-2, составляет
2
A1 2 A
1
7
8
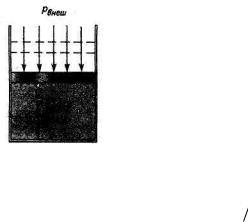
Рассмотрим работу, которая совершается при расширении газа, рис. 1.
Рис. 1.
При перемещении поршня вверх на малое расстояние
dx , изменяя при этом объѐм на величину |
dV Sdx , |
газ |
совершает против внешнего давления |
pвнеш Fвнеш |
S |
элементарную работу |
|
|
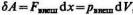 .
.
Поэтому можно записать:
A
pdV
.
(4)
Давление р газа всегда положительно. Поэтому при расширении газа ( dV 0 ) газ совершает положительную работу ( A 0 ). Если газ сжимается, то dV 0 и A 0 . В этом случае положительную работу над газом совершают силы внешнего давления. Формула (4) справедлива не только для газа или жидкости, но и для твердого тела при его расширении или сжатии под действием внешнего давления, равномерно распределенного по поверхности тела.
8
9
3. Графическое изображение термодинамических процессов
Графически можно изображать только равновесные процессы (для этих процессов значения параметров во всех частях тела одинаковы).
Для неравновесных, процессов нельзя говорить о параметрах состояния для всего тела (или системы) в данном состоянии. Значения параметров в разных частях тела различны. Поэтому графическое изображение неравновесного процесса невозможно. Поясним сказанное на примере сжатия газа в цилиндре с подвижным поршнем (рис. 1). Пока поршень неподвижен, газ находится в равновесии с внешней средой. Давление, температура и плотность газа во всех частях объема цилиндра одинаковы. Когда поршень начинает перемещаться под действием внешних сил, изменения давления газа распространяются в нем со скоростью звука. При сжатии газа под поршнем образуется область повышенного давления. Нарушается равенство давлений во всех частях объема газа и тем сильнее, чем с большей скоростью движется поршень. Такое состояние газа является неравновесным и не может оставаться долго после остановки поршня. Этот пример показывает, что сжатие газа поршнем — неравновесный процесс.
В некоторых случаях неравновесностью реальных процессов можно пренебречь. В рассмотренном примере это можно сделать, если скорость движения поршня значительно меньше скорости звука в газе и размеры цилиндра невелики.
9
10
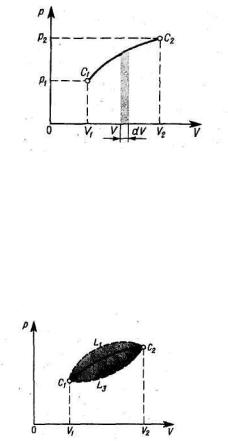
На диаграмме р — V элементарная работа
A pdV
графически изображается площадью криволинейной трапеции, закрашенной на рис. 2.
Рис. 2.
Работа, совершаемая системой в процессе С1С2, равна
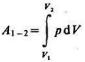 .
.
Эта работа зависит от вида процесса, рис. 3.
Здесь на рис. 3 имеем
Рис. 3.
A |
A |
L |
L |
1 |
3 |
.
После завершения системой процесса по замкнутой кривой C1L1C2L2C1, при котором система возвратилась в исходное состояние С1 полная работа AL1 L3 не равна нулю.
10
