Экспериментальная оценка мультипликативной систематической погрешности на основе методов замещения и противопоставления.

При выполнении данной лабораторной работы студент добивается следующих целей:

- закрепляет знания, полученные на лекциях по дисциплине «Метрология, взаимозаменяемость и стандартизация»» «Теоретическая метрология»;

- развивает умения по постановке измерительного эксперимента, реализующего методы замещения и противопоставления, организации и последующего его проведения:

- закрепляет навыки по обработке результатов измерений;

- осваивает приемы исключения мультипликативной систематической погрешности из результатов измерений;

- развивает умения надлежащим образом оформлять выполненную лабораторную работу.

Теоретические основы лабораторной работы.

И метод замещения и метод противопоставления реализует принцип тождественного преобразования путем последовательного использования прямого и обратного преобразования по схеме

Где - прямое преобразование измеряемой величины в результат измерения;

- обратное преобразование результата измерения в оценку измеряемой величины.

Абсолютного тождества быть не может из-за невозможности учета всех факторов, влияющих на результат прямого и обратного преобразования. Методы замещения и противопоставления применимы для СИ, основанных на нулевом принципе измерения, в котором можно менять местами материальный объект -- носитель измеряемой величины и переменную образцовую меру. К таким СИ относятся, например, равноплечие рычажные весы, измерители электрического сопротивления, использующие равноплечные мостовые схемы и т.п.

Рассмотрим сначала использование метода замещения для определения мультипликативной погрешности результата измерения электрического сопротивления с помощью равноплечной мостовой схемы, показанной на рис.4.1.

Рис.4.1

Известно, что условие равновесия мостовой схемы определяется уравнением

(4.1) где r - измеряемое электрическое сопротивление;

- переменное образцовое электрическое сопротивление;

- постоянные электрические сопротивления;

r - составляющая, обусловленная действием возмущающих факторов (паразитные сопротивления).

Разрешая уравнение (4. 1 ) относительно 7 , получим

(4.2)

где y(r) - результат измерения электрического сопротивления r ,

-- коэффициент чувствительности мостовой схемы,

q - размер единицы электрического сопротивления, воспроизводимой мостовой схемой,

- аддитивная погрешность (смещение нуля).

Оставляя - неизменным, заменим измеряемое электрическое сопротивление r переменным образцовым электрическим сопротивлением , и с его помощью реализуем равновесие моста. Уравнение равновесия будет иметь вид:

(4.3) Разрешим это уравнение относительно , . В результате получим

(4-4)

где - аддитивная погрешность.

Из уравнения (4.4) следует оценка коэффициента чувствительности

Теперь оценка мультипликативной погрешности определяется следующим выражением

Но истинное значение электрического сопротивления r неизвестно. Поэтому воспользуемся уравнением (4.2) и получим

(4.5)

где

Аддитивную составляющую можно оценить на основе баланса измеряемых величин.

Рассмотрим теперь метод противопоставления. Его суть заключается и том, что при замене местами сопротивлений и r уравнение (4.1) в состоянии равновесия мостовой схемы запишется следующим образом:

Разрешая его относительно , получим

(4.6) где - аддитивная погрешность.

Разделим уравнение (4.2) на уравнение (4.6). В результате получим выражение для оценки параметра k

Теперь оценка мультипликативной погрешности будет равна

Рассмотрим определение интервальных оценок мультипликативной систематической погрешности и дисперсии при многократных измерениях на основе метода замещения. Используя для обозначения случайных результатов измерения большие буквы, выражения (4.2) и (4.6) запишем следующим образом

Где - центрированная случайная погрешность с дисперсией D_e. Тогда математические ожидания и дисперсии случайных результатов измерений Y(r) и Y₁(r) ,будут равны.

(4.7)

Обратимся теперь к оценке (4.5) как к случайной величине

Найдем математическое ожидание и дисперсию этой оценки с учетом выражений (4.7)

Таким образом, оценка мультипликативной систематической погрешности является несмещенной и имеет дисперсию, равную D_e. .

Для оценки неизвестной дисперсии D_e. и более точной оценки мультипликативной систематической погрешности выполним многократные измерения в соответствии со следующим планом измерения и получим совокупность результатов измерений

При допущении, что многократные измерения являются нормально распределенными, равноточными и некоррелированными их обработку проведем на основе следующих алгоритмов:

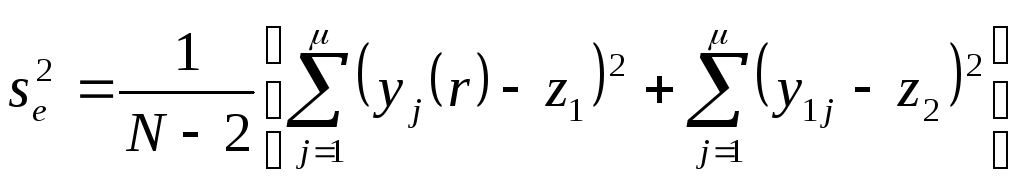
N=2

Запишем выражения для интервальных оценок:

- интервальная оценка для мультипликативной систематической погрешности,

- интервальная оценка для дисперсии,

где есть решение уравнения

- табулированный интеграл вероятности распределения Стьюдента c N-2 ст. свободы.

Справочное обеспечение лабораторной работы

Справочное обеспечение лабораторной работы в варианте использования калькуляторов сводится к табулированным значениям интеграла вероятности распределения Стьюдента , представленным табл. 4.1

Таблица 4.1

Pдов n	0,90	0,95	0,975
2	1,89	2,92	4,31
3	1,64	2,35	3,18

Для определения интервальной оценки дисперсии потребуются табулированные значения функции распределения F(q;N-2), представленные в таблице 4.2

Таблица 4.2

N	Рдов	0,90	0,95	0,98
2	q1	0,352	0,216	0,115
	q2	7,814	9,348	11,345
3	q3	0,711	0,484	0,300
	q4	9,488	11,143	13,277

В варианте обработки многократных измерений с использованием статистического пакета используются полные таблицы интеграла вероятности центрального распределения Стьюдента и функции центрального - распределения с числом степеней свободы до v=11.

Форма представления выполненной лабораторной работы.

Отчет о выполнении лабораторной работы должен включать следующие пункты:

• Априорные данные

• вид измеряемой величины,

• средство измерения.

• Планы измерений:

• для оценки мультипликативной систематической погрешности методом замещения

• для оценки мультипликативной систематической погрешности методом противопоставления.

• Результаты многократных измерений:

• для метода замещения;

• для метода противопоставления.

• Обработка многократных измерений:

• алгоритмы обработки многократных измерений (при использовании микрокалькулятора);

• точечные и интервальные оценки мультипликативной систематической погрешности и дисперсии для метода замещения;

• точечная оценка мультипликативной систематической погрешности для метода противопоставления;

• алгоритм исключения мультипликативной систематической погрешности. Интервальные оценки должны иметь вероятностную интерпретацию.