Вариант типового расчета для 2 модуля

1. Найти пределы:

1.1 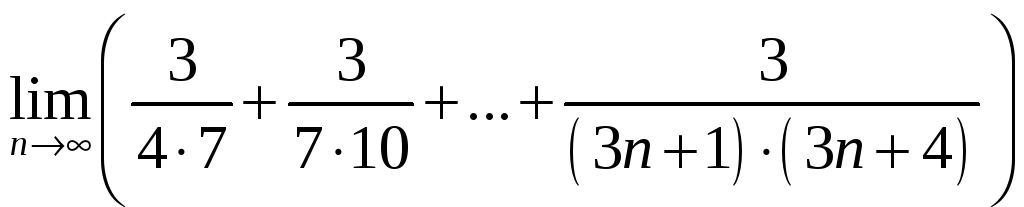1.2

1.3 1.4

1.5 1.6

1.7* а) б) в)

2. Исследовать функции на непрерывность и построить их графики:

2.1 2.2 2.3*

3.1 Продифференцировать функцию . Упростить полученное выражение.

3.2 Продифференцировать функции:

а) б)

3.3* Найти производную функции , пользуясь непосредственно определением производной.

3.4 Найти пределы функций, используя правило Лопиталя:

а) б)

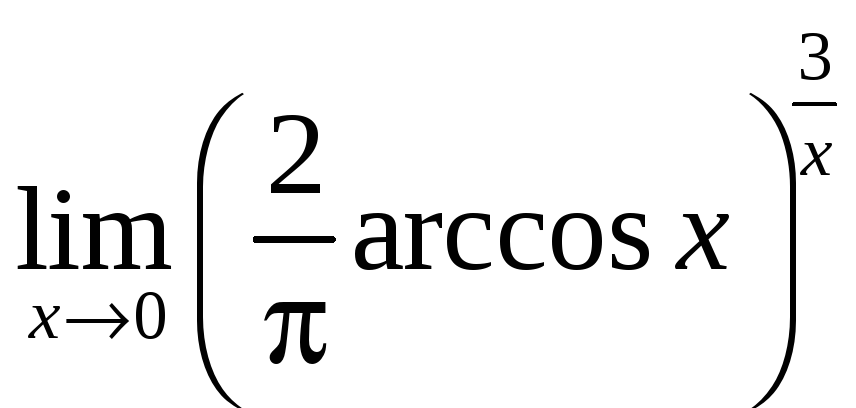
3.5* Записать формулу для производной порядка функции .

4. Провести полное исследование функций и построить их графики:

а) б) * .

5. а) Известно, что сумма двух положительных чисел и равна 20. При каких значениях и величина будет наибольшей?

б) * Определить наибольшее отклонение от нуля функции на отрезке [0;].

в)* Криволинейная трапеция ограничена кривой и отрезками прямых . В какой точке кривой следует провести касательную, чтобы она отсекала от криволинейной трапеции обычную трапецию наибольшей площади?

Методические указания

Типовой расчет содержит пять заданий. Отмеченные “звездочкой” задачи сложнее остальных и выполняются по желанию.

Задача 1.1 Найти предел последовательности .

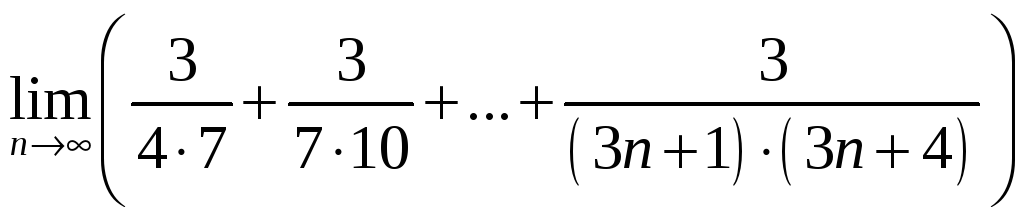Решение. Представим дробь в виде разности двух дробей . Тогда -ый член последовательности можно переписать в виде

.

Дробь является бесконечно малой при , поэтому

.

Задача 1.2 Найти предел функции .

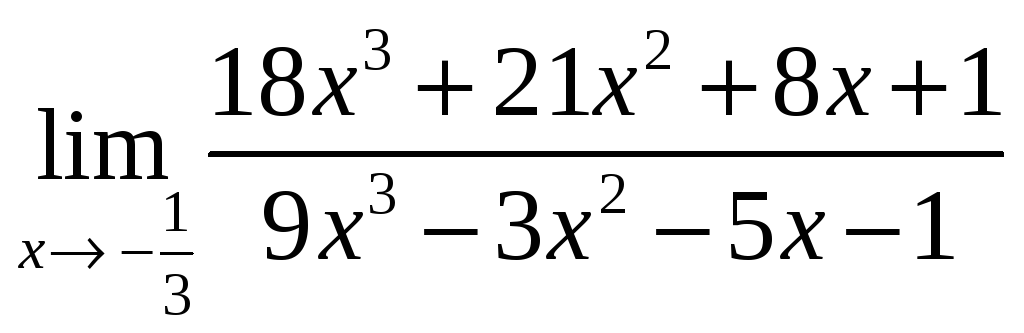Решение. Числитель и знаменатель дроби стремятся к 0 при , то есть получается неопределённость вида . Разложим на множители числитель и знаменатель дроби, воспользовавшись информацией о том, что один корень уже известен, тогда

.

Задача 1.3 Найти предел функции .

Решение. Делением числителя дроби на знаменатель выделим целую часть . Таким образом, .

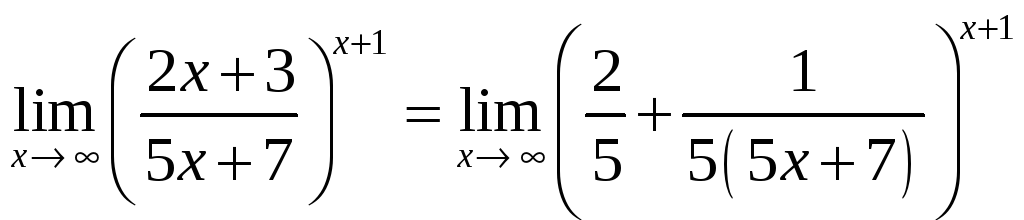Дробь является бесконечно малой при , тогда при получим 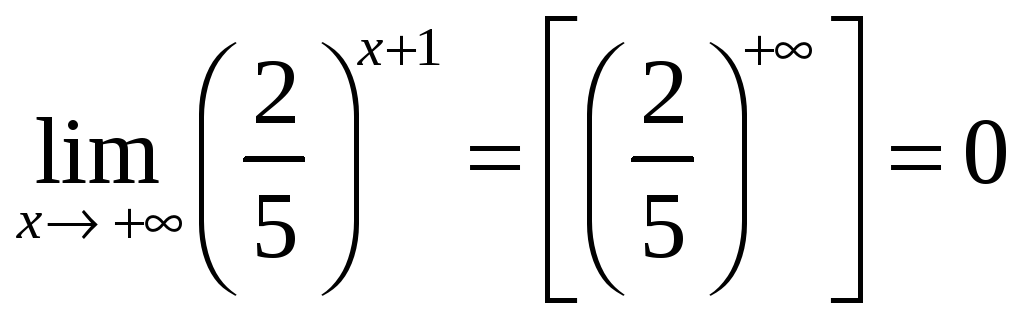, при .

Задача 1.4 Найти предел функции .

Решение. По формулам приведения , поэтому . Используя второй замечательный предел, получим . Так как непрерывная на всей числовой оси функция, поменяем местами знаки вычисления предела и показательной функции: . Здесь было использовано правило замены на эквивалентные бесконечно малые функции: при .

Задача 1.5 Найти предел функции .

Решение. Для раскрытия неопределённости вида сделаем замену переменной , тогда . Функцию преобразуем следующим образом 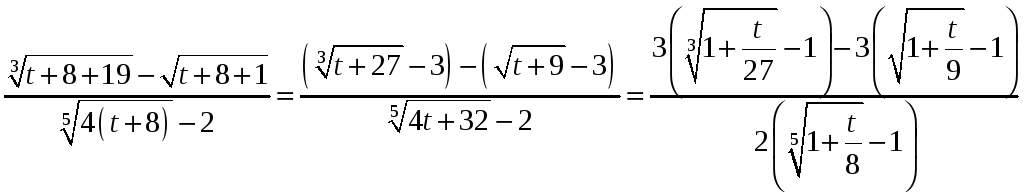. Далее можно использовать эквивалентные бесконечно малые функции . Предел разности функций запишем в виде разности пределов и получим:

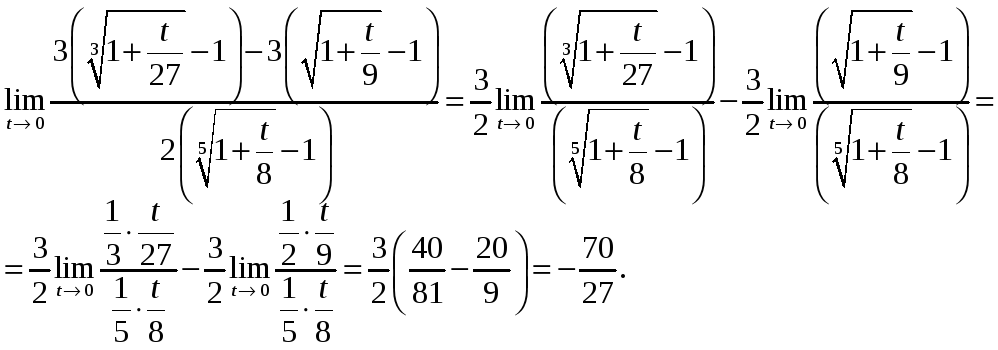
Задача 1.6 Найти предел функции .

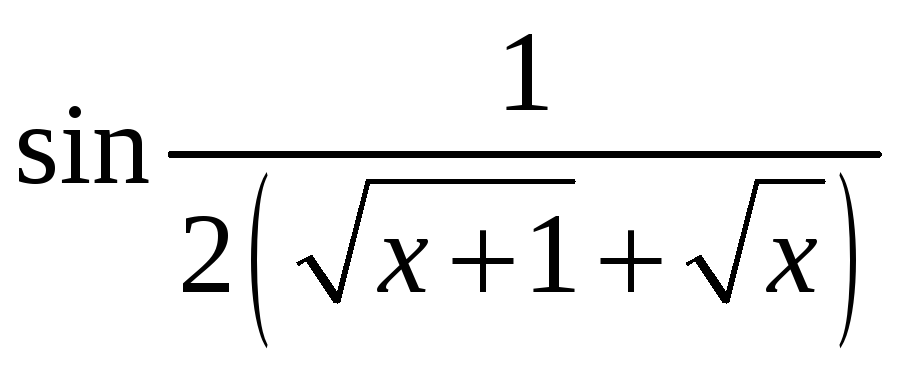Решение. Заметим, что при функции и не имеют предела, а принимают все возможные значения от -1 до 1. Воспользуемся формулой для разности синусов и получим: . Функция ограничена, а аргумент функции преобразуем, домножив числитель и знаменатель на . Полученная функция является бесконечно малой при . Произведение ограниченной функции на бесконечно малую будет бесконечно малым, а, значит, .

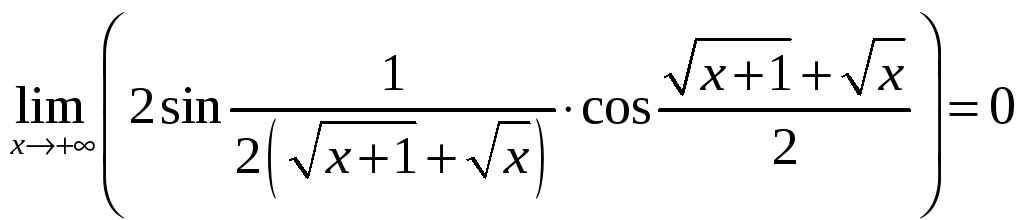Задача 1.7* а) Найти предел функции .

Решение. Для раскрытия неопределенности вида сделаем замену переменной . Тогда . Разложим по формуле бинома Ньютона , . Для вычисления предела будем пренебрегать бесконечно малыми функциями более высокого порядка, чем . Тогда .

Задача 1.7* б) Найти предел функции .

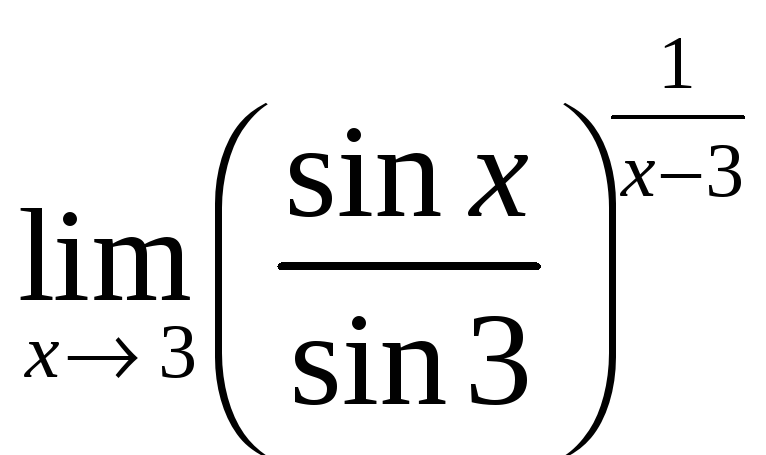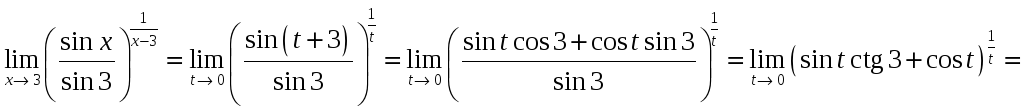
Решение. Для раскрытия неопределенности вида сделаем замену переменной , тогда Здесь функция является бесконечно малой более высокого порядка, чем , поэтому ею можно пренебречь. Используя первый замечательный предел , найдем .

Задача 1.7* в) Найти предел функции .

Решение. Раскроем неопределенность вида , введя новую переменную . Далее домножим числитель и знаменатель на выражение, сопряженное числителю, и получим . Бесконечно малую функцию при заменим на эквивалентную . Тогда .

Задача 2.1 . Исследовать функцию 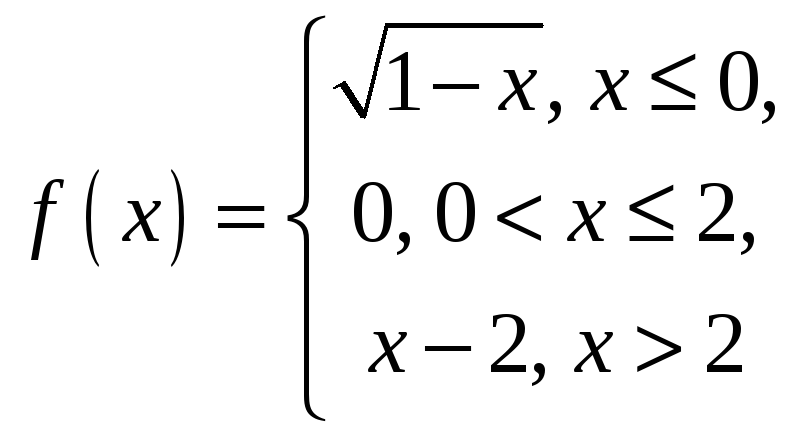на непрерывность и построить её график.

Решение. Функция определена на всей числовой оси, но не является на ней непрерывной, так как эта функция неэлементарная. Она задана тремя различными формулами для разных интервалов изменения аргумента и может иметь разрывы в точках и , где меняется её аналитическое выражение. Исследуем поведение функции при приближении к точке слева и справа: , а . Значит, это точка разрыва 1 рода (или конечного разрыва). Далее , , то есть в точке функция непрерывна. График функции представлен на рисунке 1.

y

1

2

x

Рис.1

Задача 2.2 Исследовать функцию на непрерывность и построить её график.

Решение. Разложим знаменатель этой элементарной функции на множители и получим . Эта функция определена и непрерывна во всех точках области определения: . В точках и она не определена, поэтому имеет в них разрывы. Вычислим лево и правосторонние пределы функции в этих точках: , . Следовательно, в точке функция имеет конечный разрыв, её скачок . . Следовательно, в точке функция имеет бесконечный разрыв (или разрыв 2 рода). График функции представлен на рисунке 2.

Y

1/8

-1/8

-5

3

X

Рис.2

Задача 2.3* Исследовать функцию на непрерывность и построить её график.

Решение. Элементарная функция определена и непрерывна на всей числовой оси, кроме точек . Так как выполнено условие , то функция является четной, а, значит, можно исследовать на разрыв только одну точку, например, . Вычислим односторонние пределы функции в этой точке.

Так как , то .

Далее , поэтому .

Следовательно, точка , как и точка , является точкой разрыва 2 рода. График функции представлен на рисунке 3:

3

-3

Y

X

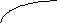
Рис.3

Задача 3.1 Продифференцировать функцию . Упростить полученное выражение.

Решение. Продифференцируем функцию как сумму двух функций и упростим результат: .

Задача 3.2 а) Продифференцировать функцию .

Решение. Вначале преобразуем функцию согласно свойствам логарифмов , а затем применим логарифмическое дифференцирование и найдем: , откуда .

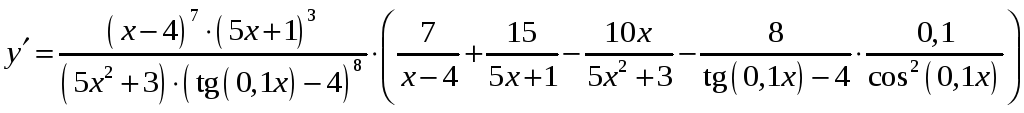Задача 3.2 б) Продифференцировать функцию .

Решение. Запишем функцию в виде показательной , а затем продифференцируем, используя теорему о производной произведения: . Теперь вернемся к первоначальной форме записи функции и получим ответ .

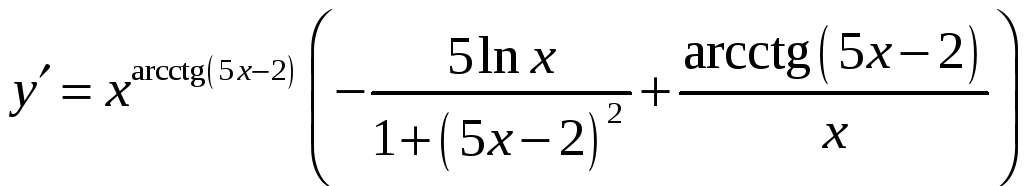Задача 3.3* Найти производную функции , пользуясь непосредственно определением производной.

Решение. Дадим приращение , тогда получит приращение : , откуда . Исходя из определения производной, найдем: 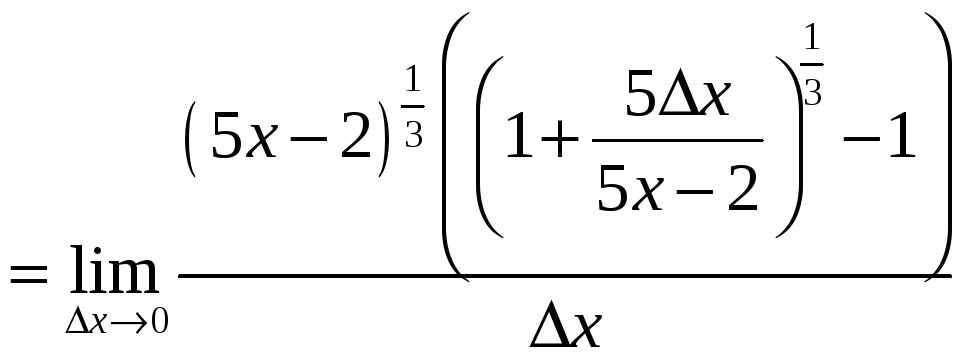. Заменим бесконечно малую функцию 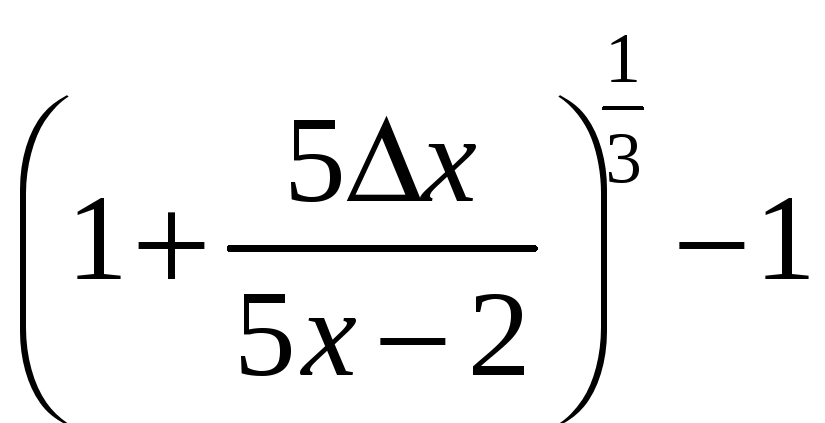на эквивалентную и получим .

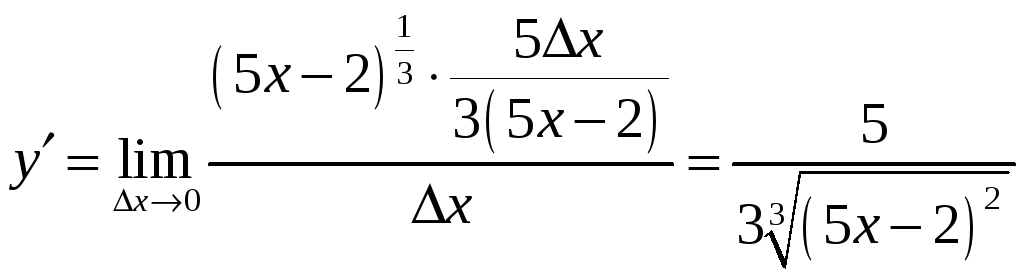Задача 3.4 а) Найти предел , используя правило Лопиталя.

Решение. Предел представляет собой неопределённость вида , поэтому преобразуем функцию к виду дроби, числитель и знаменатель которой стремятся к 0, а затем применим правило Лопиталя дважды:

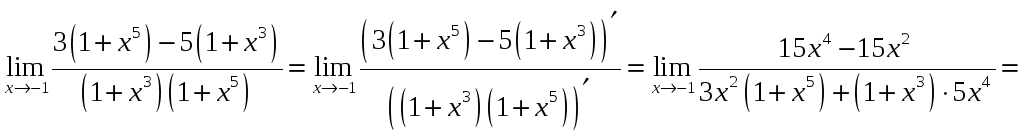
Задача 3.4 б) Найти предел , используя правило Лопиталя.

Решение. Здесь имеет место неопределённость вида . Обозначим искомый предел через и прологарифмируем функцию 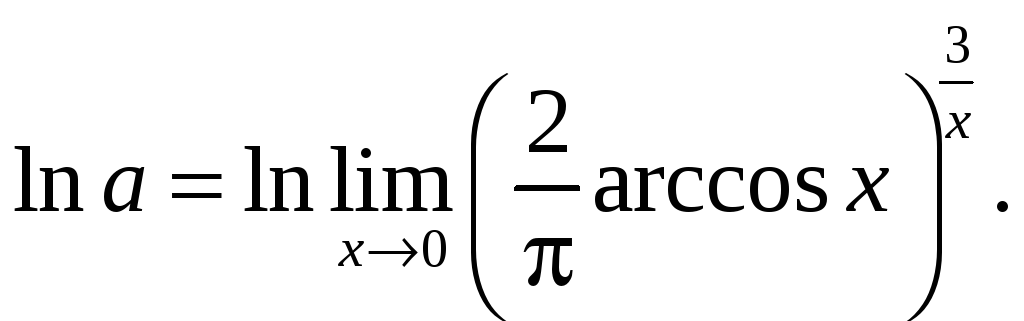Найдем предел её логарифма:

Теперь по найденному пределу логарифма функции найдем предел самой функции .

Задача 3.5* Записать формулу для производной порядка функции .

Решение. Дифференцируя последовательно раз данную функцию, найдем , , ,…,.

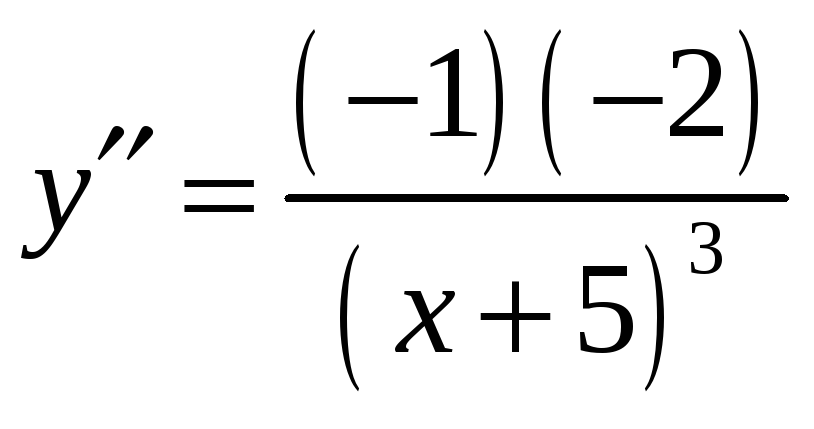Задача 4. Провести полное исследование функций и построить их графики. Исследование функций рекомендуется проводить по следующей схеме:

1. Найти область определения функции.

2. Проверить, является ли функция чётной (нечётной), а также периодической, и указать, как эти свойства влияют на вид графика функции.

3. Исследовать функцию с помощью первой производной: найти интервалы монотонности и экстремумы функции.

4. Исследовать функцию с помощью второй производной: найти интервалы выпуклости (вогнутости) и точки перегиба функции.

5. Проверить наличие вертикальных, горизонтальных и наклонных асимптот графика функции.

6. Найти точки пересечения графика с координатными осями и (при необходимости) найти значения функции в некоторых дополнительных точках.

а) Провести полное исследование функции и построить её график.