4. Функциональное диагностирование при поиске отказов в пространстве параметров

При диагностировании в пространстве параметров отказ моделируется как отклонение значения какого-либо параметра системы от номинального значения. Так, например, для линейной системы элементов системных матриц от номинала:

(6.7)

а для нелинейной системы

При этом в данном случае число типов M однократных отказов равно числу параметров системы.

Применим рассмотренные в предыдущем разделе алгоритмы при диагностировании в пространстве параметров. Пусть параметр принадлежит к числу диагностируемых. Разделим интервал значений параметра наl подынтервалов . С каждым из подынтервалов соотнесем наблюдатель, основанный на модели системы при значении параметра. Будем учитывать, что в рассматриваемом случае наблюдатели не формируют оценку величины отказанепосредственно, однако она может быть получена в соответствии с выражением:

,

где ,- номинальное значение параметра.

Проанализируем эффективность алгоритмов диагностирования с независимыми и взаимодействующими наблюдателями на следующем примере.

Пример 6.3. Рассмотрим в качестве примера модель водяной торпеды, описываемую нелинейным уравнением:

,

где – момент инерции торпеды,– угол поворота торпеды.

Для этого примера в среде Simulink было проведено моделирование задачи диагностирования одиночного отказа в пространстве параметров с использование двух алгоритмов – независимые наблюдатели и взаимодействующие наблюдатели, соотносимые с техническими состояниями. Моделировался перемежающийся отказ в виде последовательности отклонений параметра от номинального значения и возвращения к нему (первые диаграммы на рис. 6.19 а и б). На вход системы подавался синусоидальный сигнал с амплитудой 0,5. Наибольшую эффективность продемонстрировал второй алгоритм. На рис. 6.18б приведены соответствующие ему результаты моделирования (коэффициенты уверенности К₀ и К₁ для работоспособного и неработоспособного технических состояний) задачи диагностирования. Видно, что в отличие от случая независимых наблюдателей (рис. 6.19а) средства диагностирования формируют значения коэффициентов уверенности, адекватные реальным техническим состояниям.

Чтобы количественно оценить степень адекватности результатов в обоих случаях (примеры 6.2 и 6.3), по полученным реализациям были рассчитаны вероятности правильного диагностирования. При этом анализировались временные интервалы, на которых система была неработоспособна. Для них вычислялась суммарная длительность подынтервалов, где происходило ошибочное формирования сигнала о работоспособном состоянии (коэффициент уверенности для работоспособного состояния достигал установленного порогового значения А = 0.9). Результирующая вероятность определялась как отношение этой величины к суммарной длительности рассматриваемых интервалов неработоспособности. Таким образом, для метода с независимыми наблюдателями были получено значение P = 0,09, а для метода с взаимодействующими наблюдателями – P = 0,8.

Кроме приведенных характеристик, по результатам моделирования для обоих методов были определены минимальные величины диагностируемых отказов, которые определялись в зависимости от величины входного сигнала. Эти результаты, как и предыдущие, свидетельствуют о преимуществах метода, использующего взаимодействующие наблюдатели.

Принятие решений об отказах с учетом их эквивалентности и доминирования

Правила принятия решений об отказах в основном уже были рассмотрены в подразделе 6.2. Однако, как будет показано ниже, в некоторых случаях использование описанных правил будет приводить к ошибкам диагностирования, когда не бракуется отказавшая система. Ошибки будут возникать в тех случаях, когда среди рассматриваемых отказов есть эквивалентные или связанные отношением доминирования. Введем на множестве отказов отношения эквивалентности и доминирования [31], предварительно напомнив определение эквивалентных динамических систем, т.е. отношения эквивалентности на множестве динамических систем.

Определение 6.1. Две динамические системы Σ₁ и Σ₂ эквивалентны, если для каждого внутреннего состояния системы Σ₁ найдется такое внутреннее состояние системы Σ₂, находясь в которых, обе системы в ответ на одинаковые входные сигналы генерируют одинаковые выходные сигналы.

Определение 6.2. Два отказа исистемы Σ эквивалентны, если соответствующие им неисправные модификации Σ₁ и Σ₂ системы Σ эквивалентны.

Предположим теперь, что в рассматриваемый перечень отказов вошли два эквивалентных отказаи. При появлении в системе одного из этих отказов соответствующие этим отказам наблюдатели будут генерировать одинаковые невязки низкого уровня. В результате и соотносимые с этими отказами коэффициенты уверенности также будут одинаковыми и не превосходящими уровня 0,5, т.к. по построению сумма коэффициентов уверенности должна равняться единице. В связи с тем, что назначаемое в правиле принятия решения для коэффициентов уверенности пороговое значениеA обычно близко к единице (например, A = 0,9), сигнал об отказе не будет сформирован, и произойдет ошибка диагностирования.

Таким образом, можно утверждать, что среди отказов, включаемых в рассматриваемый перечень, не должны содержаться эквивалентные, а точнее, от каждого множества эквивалентных отказов в рассматриваемый перечень должен входить лишь один представитель.

Перейдем к обсуждению отношения доминирования на множестве отказов. Физический смысл этого отношения сводится к следующему. В случае присутствия в системе двух отказов, связанных отношением доминирования, доминирующий отказ полностью маскирует проявление в работе системы доминируемого отказа. Упрощенно отношение доминирования можно определить как частичную эквивалентность, а точнее, как эквивалентность на некоторой (но не любой) входной последовательности. В результате, если на входе системы присутствует эта последовательность, то отказы, принадлежащие отношению доминирования и входящие в перечень рассматриваемых отказов, не будут обнаружены по причине, рассмотренной выше для эквивалентных отказов. Таким образом, также возникает ошибка диагностирования. При появлении на входе системы последовательности, на которой эти отказы не эквивалентны, произойдет правильное обнаружение и диагностирование присутствующего в системе отказа. Таким образом, ошибка диагностирования будет существовать, пока на входе системы существует не различающая отказы последовательность.

Избежать ошибок диагностирования можно, поступив также как и в случае эквивалентных отказов, т.е. оставив из каждой пары таких отказов лишь одного представителя – доминирующий отказ. Однако при этом отказ, исключенный из рассматриваемого перечня, будет неправильно диагностироваться. Возможен также и другой подход, когда заданное множество рассматриваемых отказов разбивается на подмножества таким образом, чтобы каждое из подмножеств не содержало отказов, находящихся в отношении доминирования. Для каждого из подмножеств по описанным в предыдущих подразделах правилам формируются свои средства диагностирования. Результаты диагностирования, получаемые независимо для каждого из подмножеств отказов, далее должны дополнительно анализироваться в случае их одновременного срабатывания при отказах, связанных отношением доминирования.

Остается неосвещенным вопрос о том, каким образом определять отказы, принадлежащие отношению доминирования. Рассмотрим этот вопрос, не претендуя на исчерпывающее решение вопроса. Для простоты рассмотрим случай диагностирования в пространстве параметров. Ясно, что необходимым условием диагностируемости отказа является чувствительность выхода диагностируемой системы к этому отказу. Причем, если от анализируемого параметра зависят только матрицы F и G, то для диагностируемости необходимо, чтобы вектор состояния системы был чувствителен к значению рассматриваемого параметра. Продифференцировав по параметру обе части уравнения динамики в (6.1), перейдем к уравнению чувствительности системы:

,

где – функция чувствительности по параметру. Очевидно, что ненулевая чувствительность системы возможна лишь при ненулевых производныхи. Именно эти матрицы и составляют основу дальнейшего анализа.

Проанализируем уравнение динамики из (6.1). Для этого разложим матричные функции ив ряды Тейлора по компонентам вектора параметров в окрестности номинальной точкии ограничимся их линейными частями:

,

,

где использованы следующие обозначения: – номинальное значениеi-й компоненты вектора ,. Обозначим. Подставим полученные выражения в уравнение динамики из (6.1):

.

Рассмотрим иллюстративный пример.

Пример 6.4.

Пусть динамическая система характеризуется следующими матрицами:

.

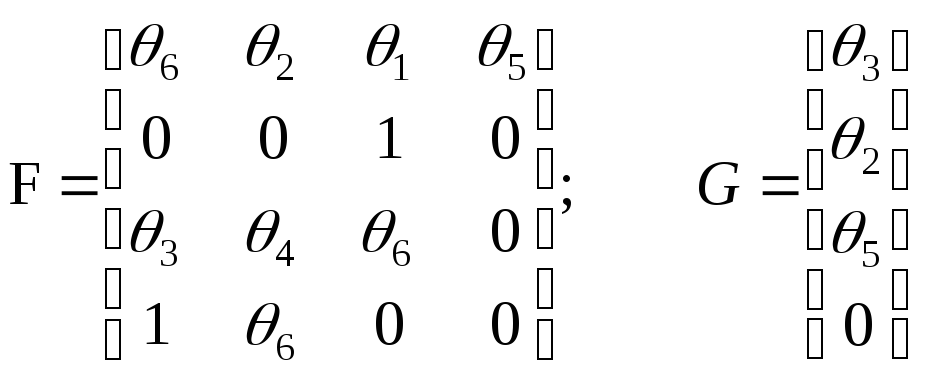Определим для этой системы матрицы :

Итак, набор матриц характеризует чувствительность системы к соответствующим отказам. Определим на этом множестве отношение частичного порядка по следующему правилу. Пусть каждый ненулевой столбец матрицыпредставляет собой линейную комбинацию столбцов матрицы. Будем обозначать этот факт. Поскольку между множествами матрици отказов существует взаимнооднозначное соответствие, то определенное отношение переносится и на множество отказов. Будем говорить об отношении доминирования на множестве отказов и записывать, если.

Нетрудно видеть, что, если диагностируемая система на некоторой входной последовательности чувствительна к отказу , то она будет чувствительна на этой входной последовательности и к отказу, и наоборот, если система на некоторой входной последовательности нечувствительна к отказу, то она будет нечувствительна на этой входной последовательности и к отказу.

Если отношение включения между матрицами выполняется в обе стороны и, то отказы эквивалентны.

Пример 6.5. Построим для примера 6.4. граф отношения доминирования (рис.6.20.). На этом графе в частности отмечено, что отказы иэквивалентны.

Нечеткое техническое состояние. В заключении настоящего подраздела обсудим еще один аспект ФД, связанный с понятием технического состояния системы или элемента. Это понятие мы широко использовали на протяжении всего предыдущего текста и при этом понимали под техническим состоянием характеристику системы, которая могла принимать ряд (лингвистических) значений: «работоспособное», «неработоспособное при отказе 1», «неработоспособное при отказе 2» и т.д. Сначала о традиционной трактовке этого понятия. Она иллюстрируется на рис. 6.21 а. Здесь предполагается, что техническое состояние системы определяется одним параметром Θ, а зоны работоспособных и неработоспособных состояний системы (значений параметра Θ) отмечены прямоугольниками разного цвета. Принципиальным является то, что эти зоны не пересекаются. Однако возможен и другой взгляд на понятие технического состояния, основанный на понятии нечеткого множества (рис. 6.21 б). В этом случае множества работоспособных и неработоспособных технических состояний описываются как нечеткие и пересекающиеся с соответствующими функциями принадлежности. В результате можно говорить о «нечетком» техническом состоянии и, как следствие, о «нечетком» отказе, под который понимается переход из работоспособного нечеткого технического состояния в неработоспособное. При этом при любом значении определяющего параметра Θ = Θ´ техническое состояние объекта может быть соотнесено как с нечетким множеством работоспособных , так и с нечетким множеством неработоспособныхсостояний.

Представляется, что этот взгляд достаточно хорошо отражает сложившийся на практике инженерный подход. Действительно, инженер, руководствуясь значением параметра, который определяет техническое состояние объекта, может считать, что объект работоспособен или неработоспособен, если значение этого параметра находится в некотором диапазоне. Причем в зависимости от конкретного значения этого параметра инженер может считать, что объект работоспособен и соответственно неработоспособен в разной степени.

Учет этой позиции возможен и при использовании описанных выше алгоритмов ФД путем перехода к описанию отказов с помощью нечетких множеств, а именно, в отношении переменных , моделирующих отказ, предполагать, что они описывается лингвистическими переменными с двумя термами – «работоспособно» и «неработоспособно», для которых заданы соответствующие функции принадлежностииилииДалее эта информация может быть использована при вычислении обобщенных степеней принадлежности, где появляется в этом случае дополнительный сомножитель: