3. Функциональное диагностирование при поиске отказов в пространстве сигналов

При диагностировании в пространстве сигналов отказ моделируется как дополнительное слагаемое δ в уравнении динамики, т.е. для исходной линейной системы

или нелинейной системы

имеем:

или соответственно

.

При этом число типов M однократных отказов равно размерности n вектора состояния диагностируемой системы. Первый тип моделируется дополнительным слагаемым в первом уравнении динамики для первой компоненты вектора x, второй тип – во втором уравнении для первой компоненты вектора x и т.д. Отказы внутри типа различаются уровнем слагаемого δ.

Как следует из рис.6.11 в задаче синтеза средств диагностирования, кроме формирования правила принятия решений, необходимо определить структуру банка и самих наблюдателей. При диагностировании линейной системы уравнения наблюдателя имеют вид [1]:

для нелинейной:

При этом вектор состояния наблюдателяпредставляет собой оценку составного вектора

,

получаемого добавлением к вектору состояния диагностируемой системы переменной, моделирующей отказ. Причем с учетом предположения о постоянстве значенияуравнение для нее имеет вид:

В результате матрицы диагностируемой линейной системы при наличии в ней i-го отказа принимают вид:

где в последнем столбце матрицы динамики единицы размещаются в последней и i-й строках. При этом если в диагностируемой системе в процессе работы возникает i-й отказ, то в наблюдателе формируется оценка этого составного вектора, в том числе формируется и оценка значения переменной. Далее, пользуясь материалом предыдущего параграфа, нетрудно синтезировать средства ФД с банком из независимых наблюдателей. Однако оказывается, что при диагностировании в пространстве сигналов можно применить несколько более сложную, но зато и более эффективную организацию банка, когда оценка в каждом наблюдателе формируется с учетом оценок в других наблюдателях. Будем называть этот случай использованием банка взаимодействующих наблюдателей.

Ниже рассматриваются два алгоритма диагностирования в пространстве сигналов, предполагающие использование банка взаимодействующих наблюдателей. В первом алгоритме наблюдатели банка соотносятся с разными техническими состояниями системы, а во втором – с разными переходами между техническими состояниями. На основании невязок, формируемых при сопоставлении выходов наблюдателей и диагностируемой системы, определяются, как было уже описано выше, коэффициенты уверенности.

Основная особенность первого алгоритма заключается в том, что на каждом очередном шаге вычислений каждый из наблюдателей опирается не на автономно сформированную им частную оценку вектора состояния, а в общем случае на более точную оценку состояния, полученную в результате осреднения частных оценок по всем наблюдателям. Причем в качестве весовых коэффициентов при осреднении выступают текущие значения сформированных на данном шаге коэффициентов уверенности, о которых также можно говорить как о более точных благодаря вычислению их во всех наблюдателях при одном и том же состоянии по результатам одного шага анализа:

. (6.6)

При этом организуется нелинейная обратная связь по состоянию, и невязка (ошибка оценивания), формируемая адекватным наблюдателем, будет стремиться к нулю, а соответствующий коэффициент уверенности будет возрастать при уменьшении коэффициентов уверенности для других технических состояний. Таким образом, в выражении (6.6) относительный вес оценки, формируемой в адекватном наблюдателе, будет возрастать.

Проведем качественный сравнительный анализ методов ФД с независимыми и взаимодействующими наблюдателями, опираясь на выражение для невязки в случае независимых наблюдателей:

Очевидно, что при использовании независимых наблюдателей нельзя утверждать, что в каждый момент времени минимальная невязка всегда формируется адекватным наблюдателем. Действительно, невязка зависит не т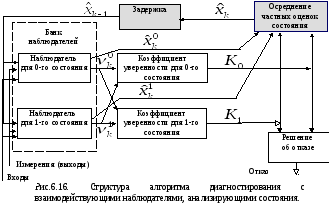олько от матрицы динамикинаблюдателя, несущей информацию об отказе, но и от текущей оценки, формируемой в наблюдателе. Ясно, что в силу различия матриц динамики траектория движения каждого наблюдателя в пространстве состояний, а значит, и результирующая оценка в общем случае будет своя, а невязка большая. Последнее касается и наблюдателя, адекватного техническому состоянию ДС, особенно во время переходного процесса. Таким образом, в общем случае отсутствуют гарантии минимальности невязки адекватного наблюдателя в каждый момент времени.

Ситуация меняется при использовании банка взаимодействующих наблюдателей, поскольку при формировании невязок во всех наблюдателях используется одна и та же оценка состояния ДС, полученная осреднением:

В результате различие невязок для разных наблюдателей определяется лишь различием матриц динамики, несущих информацию об отказе. Причем значения формируемых невязок невелики, т.к. определяются величиной одношагового прогноза состояния наблюдателя. Оба эти фактора способствуют повышению чувствительности средств ФД, что подтверждается, в частности, и результатами моделирования.

На рис. 6.16 приведена структура алгоритма для простейшего случая одного отказа, вследствие чего техническое состояние может принимать только два значения. В результате в средствах диагностирования применяются два наблюдателя. При другой интерпретации структурных блоков можно заметить сходство данного алгоритма с известным алгоритмом диагностирования стохастической системы, использующим гауссову аппроксимацию апостериорной плотности вероятности [26].

Второй алгоритм, применяющий взаимодействующие наблюдатели, похож на предыдущий, но отличается от него большей детальностью анализа поведения диагностируемой системы. Это проявляется в том, что событие, состоящее в пребывании системы в некотором неработоспособном состоянии, анализируется как два события – переход в рассматриваемое состояние и сохранение этого состояния. Для этого анализа наблюдатели настраиваются на соответствующие переходы, что означает следующее. Так, если наблюдатель настроен на переход между техническими состояниями , то он использует модель системы вj-м техническом состоянии, а при вычислениях в нем используется оценка вектора состояния, сформированная в предположении обi-м техническом состоянии:

,

где - число технических состояний, из которых возможны переходы в,- коэффициент уверенности для перехода, который вычисляется аналогично коэффициентам уверенности для технических состояний. Коэффициент уверенности для каждого технического состояния вычисляется путем суммирования коэффициентов уверенности, соответствующих переходам в это состояние:

.

На рис. 6.17 приведена структура алгоритма для простейшего случая одного отказа, вследствие чего техническое состояние может принимать только два значения, однако число рассматриваемых переходов равно трем (переход из неработоспособного состояния в работоспособное не рассматривается). В результате в средствах диагностирования применяются три наблюдателя. При другой интерпретации структурных блоков можно заметить сходство данного алгоритма с известным алгоритмом диагностирования стохастической системы, использующим полигауссову аппроксимацию апостериорной плотности вероятности [26].

Пример 6.2. Рассмотрим пример системы, заимствованный из работы [40] и характеризующийся матрицами:

По смыслу данная система представляет собой редуцированную модель контура управления самолетом по высоте, которая была получена линеаризацией уравнений движения самолета в окрестностях номинальной траектории. Это описание охватывает управляемый объект, сервопривод управления рулем, датчик высоты и регулятор.

Для этого примера в среде Simulink было проведено моделирование задачи диагностирования в пространстве сигналов. Моделировался перемежающийся (с возвратом в номинальное состояние) отказ θ в виде меандра на первом интеграторе (первая диаграмма на рис. 6.18а и 6.18б).

На вход системы подавался синусоидальный сигнал с амплитудой 0,5. На рис. 6.18 приведены временные диаграммы полученных коэффициентов уверенности для случаев использования независимых и взаимодействующих наблюдателей. Видно, что в случае независимых наблюдателей (рис. 6.18а) средства диагностирования не формируют ожидаемого результата, когда до появления отказа коэффициент К₀ должен принимать устойчивое значение, близкое к единице, а коэффициент К₁ – значение близкое к нулю. После появления отказа коэффициент К₁ должен принимать устойчивое значение, близкое к единице, а К₀ – значение близкое к нулю. При использовании взаимодействующих наблюдателей (рис. 6.18б), сопоставленных с техническим состояниями, временные диаграммы демонстрируют адекватную работу средств диагностирования. Так на интервале времени до появления отказа коэффициент уверенности К₀ для работоспособного технического состояния после переходного процесса, связанного с начальным оцениванием, принимает значение, равное единице. После появления отказа соответствующий ему коэффициент уверенности устойчиво принимает значение, близкое единице.