6. Методы функционального диагностирования

В данном разделе излагаются методы функционального диагностирования. При этом ни в кое случае не ставится цель исчерпывающего изложения известных методов ФД. Фактически приводятся лишь краткие сведения из этой области, по которым, по нашему мнению, можно составить представление о возможностях некоторых известных подходов. Задача рассматривается лишь для систем, описываемых динамической моделью. В мировой литературе задача ФД в научном плане рассматривается только для таких систем. Это, по-видимому, объясняется тем, что для более простых и более сложных систем в решении задачи ФД нет практической целесообразности.

В настоящее время в функциональном диагностировании известны два основных подхода - детерминированный и стохастический. Первый использует детерминированную модель диагностируемой системы, второй – стохастическую. Однако наряду с ними или в их рамках существуют направления, может быть, менее значимые по числу публикаций и основанные на нечетких или интервальных моделях. Возможны и смешанные, в частности, интервально-стохастические подходы. Выбор того или иного подхода, как правило, определяется содержанием априорной информации о свойствах системы и возникающих в ней отказах, имеющейся в распоряжении разработчика средств диагностирования. Так если разработчик располагает статистической информацией о поведении системы и ее отказах, то может быть применен стохастический подход. Если такой информации нет, то применяется детерминированный подход. Безусловно, между методами, соответствующими различным подходам, можно заметить определенную аналогию. Она является следствием взаимного проникновения и обогащения существующих подходов. Практически весь приводимый далее материал (за исключением последнего подраздела) соответствует детерминированному подходу.

Решение задачи ФД рассматривается как в отношении линейных, так и в отношении нелинейных динамических систем. При этом используются модели (5.4) – (5.6). Перед тем как перейти к обсуждению конкретных методов хочется еще раз напомнить о необходимости описания при построении средств диагностировании класса отказов, на которые нацелены эти средства. Без этого невозможно на завершающем этапе проектирования определить, какого же качества оказались полученные средства диагностирования, соотнеся список реально охваченных диагностированием отказов с первоначально намеченным списком.

1. Методы функционального диагностирования для обнаружения отказов

В данном подразделе в обзорном плане описываются методы обнаружения отказов. Эта задача существенно проще, нежели задача поиска отказов, когда требуется не просто забраковать диагностируемую систему как неработоспособную, но и с необходимой точностью определить местоположения отказа. Методы поиска отказов будут рассмотрены в последующих подразделах.

В рамках детерминированного подхода можно выделить определенные направления. При этом основными среди них можно считать направления, основанные на использовании алгебраических инвариантов [20], соотношений паритета, моделей объекта диагностирования [5, 8, 10, 24 – 29, 33].

Инвариант – это в данном случае некоторая характеристика объекта, сохраняющая свое значение для работоспособного объекта и изменяющая это значение при его отказе. При этом функция СД состоит в вычислении значения используемого инварианта и в сравнении этого значения с эталоном (рис. 6.1). При поиске отказов необходимо, чтобы разным отказам соответствовали бы разные значения инварианта. В качестве инвариантов могут выступать, например:

• полюса передаточной функции;

• элементы системных матриц;

• значения частотных характеристик на фиксированных частотах;

• отсчеты импульсной и переходной функций в фиксированные моменты времени.

Второе направление иллюстрируется на рис.6.2, где предполагается, что диагностируемая система линейна и описана в операторной форме. Видно, что в этом случае невязка формируется при сопоставлении преобразованных входа u и выхода y системы.

Наконец, третье направление предполагает, что невязка формируется при сопоставлении выходов диагностируемой системы и ее модели, которая может формироваться на компьютере. Простейшая иллюстрация этого подхода приведена на рис. 6.3, где предполагается, что система и ее модель, стартуя из одинаковых состояний, формируют при номинальном поведении совпадающие последовательности выходов, а при появлении отказов в системе эти последовательности расходятся (генерируется ненулевая невязкаr).

В рамках этого направления предложен целый ряд методов, ориентированных как на обнаружение отказов, так и на их поиск. Причем могут рассматриваться как линейные, так и нелинейные системы. Центральное место в известных методах занимает использование наблюдателей, которые могут строиться на основе различных принципов. Обычно выделяют наблюдатели состояния и выхода.

На рис. 6.4 представлен случай использования наблюдателя состояния по отношению к линейной системе:

Определяющим свойством подобных наблюдателей является наличие обратной связи по невязке, а также совпадение его системных матриц с системными матрицами диагностируемой системы. В результате этих свойств система и модель могут стартовать из разных состояний, и по прошествии переходного процесса не только формируют совпадающие выходные последовательности при номинальном поведении системы и расходящиеся при наличии в системе отказов, но при этом также в наблюдателе формируется оценка состояния системы .

Остановимся более подробно на вопросах синтеза наблюдателя состояния, поскольку далее при изложении материала будет использован именно этот тип наблюдателя. Процедура синтеза наблюдателя состояния для линейной системы известна, однако для полноты изложения приведем ее основные моменты. Для синтеза наблюдателя необходимо определить лишь матрицу обратной связи . Она определяется, исходя из желаемого поведения ошибки оценивания. В соответствии со структурой на рис.6.5, если диагностируемая система и наблюдатель стартуют из разных состояний, то в наблюдателе формируется оценка вектора состояния системы. Причем поведение ошибки оцениванияопределяется уравнением

.

Решение этого уравнения имеет вид:

,

где

Безусловно, эта ошибка должна достаточно быстро стремиться к нулю. Для этого матрица должна быть устойчивой, т.е. вещественные части корней ее характеристического многочлена (собственных чисел)

должны принимать отрицательные значения. Для случая, когда исходная система линейна, стационарна и наблюдаема алгоритм выбора матрицы известен и достаточно прост [1]. Он использует представление диагностируемой динамической системы в идентификационной канонической форме. Напомним свойства этого представления.

Сначала приведем короткую информацию об эквивалентных преобразованиях линейных динамических систем. Пусть рассматриваемая система описывается уравнениями:

Запишем эти уравнения в другой системе координат:

Пусть новая система координат связана с исходной неособенной матрицей преобразования T, т.е. . Тогда уравнения для преобразованной системы приобретают вид:

Отсюда, приравнивая выражения для выходов исходной и преобразованной систем, получаем:

.

Приравнивая производные от этих выходов, получаем остальные выражения:

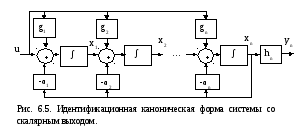
Выбирая соответствующим образом матрицу преобразования T, можно получать эквивалентные описания системы с характерными свойствами, которые называются каноническими формами. Одной из таких форм является идентификационная каноническая форма. Напомним ее свойства.

Для начала, предположим, что система имеет скалярный выход, а также для простоты и скалярный вход. Тогда она имеет структуру (рис. 6.5), в которой интеграторы вытянуты в цепочку при единственной обратной связи с выхода последнего интегратора.

При этом, например, для номинального состояния матрицы диагностируемой системы, а, значит, и соответствующие матрицы наблюдателя имеют следующий вид.

, , , ,

где – коэффициенты характеристического многочлена системы.

При такой структуре матриц

,.

Таким образом, матрица имеет вид сопровождающей матрицы, где последний столбец составлен из коэффициентов характеристического многочлена. Назначив для характеристических чисел этой матрицы желаемые значения, обеспечивающие необходимую скорость стремления к нулю ошибки оценивания, можно определить коэффициенты характеристического многочлена для, а затем и элементы матрицы обратной связи на основе соотношений.

В случае, когда диагностируемая система имеет много выходов, процедура определения матрицы обратной связи усложняется [1], хотя последовательность шагов остается прежней. Также, прежде всего, диагностируемую систему надо представить в идентификационной канонической форме, которая принимает более сложный вид (рис. 6.6). Она содержит уже не одну цепочку интеграторов с обратной связью с последнего интегратора, а несколько – по числу выходов системы. Эти цепочки с обратными связями на рисунке представлены прямоугольниками, обозначенными . Кроме того, при упорядочивании этих компонент (цепочек) по убыванию размерности выход каждой компоненты участвует в формировании выходов всех последующих. В результате, например, для номинального состояния матрицы системы, а, значит, и соответствующие матрицы наблюдателя имеют вид:

, ,,

, , ,

.

ВматрицеV единицы стоят в столбцах с номерами . ПричемИспользование этой матрицы позволяет ввести в соотношения матрицу, преобразующую вектор значений последних интеграторовв цепочках в выходной векторсистемы. Для нас важно, что ввиду неособенности этой матрицы существует возможность определения векторапо значению вектора. Отсюда следует, что задачу определения обратной связи в наблюдателе мы можем решать для каждой компоненты отдельно по выше изложенному алгоритму для системы с одним выходом.

Синтез наблюдателей выхода осуществляется по другим правилам. Теория построения наблюдателей выхода развита достаточно хорошо. На рис. 6.7 представлен случай, когда с помощью наблюдателя выхода диагностируется линейная система, однако известны алгоритмы построения таких наблюдателей и для нелинейных систем. В общем случае наблюдатель выхода имеет меньшую размерность, нежели диагностируемая система. В связи с этим на рисунке матрицы наблюдателя имеют другие обозначения (A, B и C). Возможность получения для наблюдателя меньшей размерности связана с использованием в нем преобразователей T и K. Первый из них сужает многообразие выходных последовательностей диагностируемой системы и тем самым создает предпосылки для реализации суженного многообразия наблюдателем меньшей размерности. Второй преобразователь служит той же цели, увеличивая для наблюдателя информацию о диагностируемой системе. Необходимым условием применения этих наблюдателей и одновременно их недостатком является старт диагностируемой системы и наблюдателя из согласованных состояний. В противном случае наблюдатель будет формировать ненулевую невязку r (сигнал отказа) при номинальной работе диагностируемой системы. Случай, когда преобразователь K отсутствует, а преобразователь T реализует тождественное отображение, называют дублированием.

Диагностирование с использование наблюдателей выхода применяется не только в отношении непрерывных и дискретных, но также и цифровых систем. Последний случай активно исследовался в 70-х и 80-х годах прошлого столетия. Однако предложенные тогда методы в настоящее время в определенной степени утратили свою значимость из-за практической нецелесообразности решения задач ФД для достаточно простых устройств, которые принято описывать автоматной моделью. Тем не менее, для полноты картины коротко опишем и этот подход.

Существенную роль в этом подходе [17] играет использование результатов теории помехоустойчивого кодирования двоичной информации в каналах связи. При этом под кодом понимается набор двоичных кодовых слов, которыми представляется передаваемая по каналу связи информация. При этом каждое передаваемое слово размерности n, кроме k информационных разрядов, содержит n – k дополнительных (контрольных), которые связаны с информационными некоторыми (обычно линейными) контрольными соотношениями. При передаче через канал обмена какие-то разряды слова могут искажаться под воздействием помех. Предполагается, что в результате должны нарушаться использованные при формировании кода контрольные соотношения, поэтому, проверяя их при приеме, можно обнаружить или даже исправить возникшие искажения. Определение правил выбора контрольных соотношений и составляет содержание теории помехоустойчивого кодирования. На рис. 6.8 приведен пример кодирования исходного безызбыточного кода, содержащего восемь кодовых слов, представляющих некоторую, например, текстовую информацию. Искажение даже одного бита в любом кодовом слове будет превращать это слово в другое также разрешенное слово, а, следовательно, оно будет незамеченным. Иначе обстоит дело в избыточном коде, приведенном на том же рисунке и полученном из предыдущего кода добавлением одного разряда. Причем значение дополнительного разряда дополняет число единиц исходного слова до четного. Формально в этом случае функция кодирования (контрольное соотношение) может быть записана следующим образом:

,

где использована операция  суммирования по модулю два (исключающее ИЛИ). Любое искажение одного бита в таком кодовом слове будет замечено при проверке на четность.

При формировании кода в общем случае для заданной максимальной кратности t возникающих ошибок вводят понятие расстояния между кодовыми словами (расстояние Хэмминга), определяемого как число разрядов сравниваемых кодовых слов, различающихся своими значениями. Формально это записывается так:

.

При этом нетрудно догадаться, что для обнаружения ошибок кратности, не превышающей t, кодовые слова должны находится на расстоянии . В этом случае возникающие ошибочные слова никогда не совпадут ни с каким кодовым словом. Эта ситуация иллюстрируется на рис. 6.8 а, где окружностями условно изображены множества ошибочных слов, в которые могут переходить кодовые слова 1001 и 1010, представленные центрами этих окружностей. Другим должно быть расстояние между кодовыми словами, когда ставится цель не только обнаруживать, но и исправлять все ошибки в пределах заданной кратностиt. Это расстояние должно удовлетворять неравенству . В этом случае видно (рис. 6.9 б), что окружности ошибочных слов не пересекаются между собой, а, значит, при приеме любое ошибочное слово может быть соотнесено с соответствующим кодовым словом.

Этот подход широко применяется в каналах обмена современных информационно-управляющих систем. Упрощенно его реализация представлена на рис. 6.10. Здесь в изображении линии связи опущены модули приема/передачи информации, и она представлена в виде совокупности линий (проводов), по каждой из которых передается один бит (разряд) информации. Описанный подход при желании можно трактовать как функциональное диагностирование параллельного канала обмена. Заметим, что в случае последовательного канала обмена информационные и проверочные символы передаются по каналу обмена последовательно во времени.

Применение идеи помехоустойчивого кодирования для решения задачи ФД автоматов сводилось к следующему. Помехоустойчивыми кодами кодировались внутренние состояния автомата, а реализация средств ФД представляла собой реализацию контрольных разрядов кода. Заметим, что в случае нелинейных автоматов контрольные соотношения оказывались также нелинейными.

В заключении данного параграфа заметим, что одним из важных вопросов, решаемых при синтезе средств ФД, является выбор или разработка алгоритма обработки невязки. Наличие неопределенностей, сопровождающих решение задачи ФД, делает решение этого вопроса непростым. Требуемое качество может достигаться двумя путями. Во-первых, оно может быть получено путем дополнительной обработки форми­руемого сигнала невязки. Такая обработка может производиться, например, путем усреднения значения сигнала невязки на некото­ром интервале времени, в результате чего несколько снижается эффект действия возмущений.

Второй путь состоит в использовании адаптивного порога, поскольку редко удается найти фиксированный порог, который бы обеспечил удовлетворительное качество диагностики одновременно для всех режимов работы системы. Это затруднение может быть преодолено за счет применения адаптивного порога, величина которого устанавливается с учетом измеряемых сигналов системы. Наиболее распространенный подход к выбору адаптивного порога состоит в следующем. Для текущих значений измеряемых сигналов находится верхняя граничная оценка величины невязки с учетом всех возможных значений возмущений и ошибок модели. Эта оценка и принимается в качестве значения адаптивного порога. Описанный выбор порога гарантирует качество диагностики, однако на практике такой порог может оказаться завышен­ным, так как он ориентирован на наиболее неблагоприятное со­четание значений возмущений и ошибок модели.