3. Тестовое диагностирование линейных дискретных устройств. Абстрактный подход

Рассмотрим задачу тестового диагностирования в случае, когда разработчик не может или не хочет при построении теста для устройства в целом воспользоваться (как это было в подразделе 5.2.2) тестом для его безынерционных преобразователей и определяет класс отказов как всевозможные искажения матриц системы. При этом будем предполагать, что система по-прежнему наблюдаема и управляема и что любой отказ из рассматриваемого класса приводит лишь к искажению матриц диагностируемой системы, но не выводит ее из класса линейных.

Обсуждаемый тест будет состоять из двух частей и. Обе части строятся по описанию исправной системы. Рассмотрим первую часть, под воздействием которой система последовательно проходит черезnсостояний. Пусть эти состояния образуют базис пространства состояний системы. После установки в каждое из этих состояний система находится в свободном движении (вход равен нулю) на протяженииnтактов, т.е.имеет вид:

,

где - установочная последовательность в,- входная последовательность изnнулей. Последовательностьсуществует, т.к. диагностируемая система управляема.

Вторая часть теста содержитmфрагментов (по числу входов), каждый из которых состоит из входного набораи последовательности, т.е.имеет вид:

В свою очередь, вектор состоит из нулевых компонент, кроме одной, равной единице. При этом наборсодержит единицу вi-м разряде.

Покажем, что любое неэквивалентное (приводящее к нарушению отображения вход-выход) искажение матриц F, G, H обнаруживается тестом . Предположим противное, что в системе присутствует искажение из рассматриваемого класса отказов, а реакция системы верна.

Воспользовавшись выражением (5.4) при нулевых входных последовательностях, запишем выражения для выходных последовательностей, формируемых из состояний базиса :

.

Объединяя эти выражения, получаем

где .

Аналогично для неисправной системы имеем: . Поскольку, то

. (5.6)

При этом из равенств иследует, а с учетом (5.6). Отсюда, а матрицыисвязаны соотношением

, (5.7)

где R – неособенная матрица. Поскольку , то

(5.8)

или в развернутом виде:

(5.9)

Приравнивая первые строки, получаем:

. (5.10)

Дополняя (5.9) одной строкой и рассматривая последние n строк, имеем:

Учитывая , получаем.

Отсюда

. (5.11)

Покажем, как получить соотношение для и, опираясь на результаты тестирования в части. Запишем выходную реакцию устройства на последовательностьвоспользуемся соотношениями (5.4). Дополним (5.4) одной строкой и рассмотрим последниеn строк. Приравнивая выходные последовательности, получаем:

.

Воспользовавшись соотношениями (5.7), (5.8) и (5.11), получаем:

или

.

Приравнивая вторые слагаемые левой и правой частей и умножая слева на , получаем:

. (5.12)

Из выражений (5.7), (5.10), (5.11) и (5.12) следует, что исправная и неисправная системы являются эквивалентными, а, значит, наше предположение о наличии в диагностируемой системе неэквивалентного искажения неверно.

Таким образом, тест обнаруживает любые неэквивалентные искажения матриц диагностируемой системы.

4. Тестовое диагностирование аналоговых линейных устройств

Ранее обсуждавшиеся средства тестового диагностирования в случае аналоговых устройств могут быть реализованы по-разному. Если эти средства являются внешними, входящими, например, в состав некоторого стенда, на котором тестируется рассматриваемое устройство, то они могут быть исполнены на основе персонального компьютера (рис. 5.4).

При этом средства должны содержать ЦАП, преобразующий генерируемый в ПК цифровой тестовый сигнал в аналоговый, а также АЦП, преобразующий аналоговый сигнал реакции устройства в цифровой.

Методы построения тестов могут быть различными. Для линейных устройств может использоваться, в частности, и частотный подход, заключающийся в снятии амплитудно-частотной характеристики устройства или в измерении ее только на резонансных частотах. Однако могут быть и другие подходы, например, связанные с использованием специальных режимов, в частности, режима свободного движения устройства (так н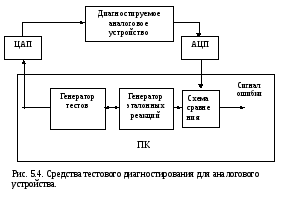азываемое модальное диагностирование). При реализации этого метода можно обойтись без ПК и реализовать его с использованием встроенных средств. Рассмотрим его для линейного устройства, которое описывается матричным дифференциальным уравнением:

, ,

где F(t) – - матрица;G(t) – - матрица, H(t) – - матрица, x(t)  n1-матрица (n-мерный вектор),  m1-матрица, y(t)  p1-матрица.

При этом в свободном движении уравнения упрощаются:

, , (5.13)

Предварительно напомним некоторые сведения из теории обыкновенных дифференциальных уравнений. Рассмотрим матричное однородное линейное дифференциальное уравнение (систему однородных линейных дифференциальных уравнений) (5.13).

Пусть уравнение (5.13) стационарно, т.е. F(t)=F. Покажем, что его решение в этом случае имеет вид

, (5.14)

где экспонента с матричным показателем представляется в виде бесконечного ряда

(5.15)

Из (5.15) следует очевидное выражение для производной по t от матричной экспоненты

.

Продифференцировав обе части равенства (5.16) и подставив результат вместе с исходным выражением в (5.13), получим тождество. Таким образом, выражение (5.14) является решением уравнения (5.13).

Теперь вспомним понятия собственного вектора и собственного числа. Собственный вектор h матрицы F – это вектор, в результате умножения которого на матрицу F получается пропорциональный ему вектор, т.е.:

. (5.16)

Преобразуем это уравнение:

. (5.17)

Данное уравнение имеет ненулевое решение, если определитель матрицы равен нулю, т.е.:

.

Корни последнего уравнения называются собственными числами.

В результате решения уравнения (5.17) для каждого из собственных чисел получаем соответствующий собственный вектор .

Теперь о сути метода модального диагностирования. Весь тестовый эксперимент состоит из n шагов (по числу собственных векторов). На каждом шаге в диагностируемое устройство заносятся новые начальные условия, совпадающие со значением очередного собственного вектора. При этом начальное условие, заносимое устройство диагностирования, является некоторой функцией от этого собственного вектора.

На основании выражения (5.14) и с учетом равенства начальных условий некоторому собственному вектору имеем:

.

С учетом (5.18) получаем:

.

В результате выражение для выхода имеет вид:

.

Таким образом, эталонная реакция может быть сформирована устройством первого порядка.