2. Математические модели объектов диагностирования

1. Модели безынерционных преобразователей

При построении средств диагностирования сразу встает вопрос об описании объекта или, как принято говорить, о его модели (математической модели). Модель потребуется в любом случае независимо от того, будем ли мы осуществлять процесс построения вручную или воспользуемся какими-либо автоматизированными средствами. Далее нам придется на языке выбранной модели описать рассматриваемые отказы. Всё вместе – модели объекта и отказов – иногда называют диагностической моделью объекта. Может оказаться, что средствами выбранной для описания объекта модели затруднительно или даже невозможно описать рассматриваемые отказы. В этом случае придется изменить свой выбор в пользу другой модели объекта.

Надо сказать, что многообразие возможных моделей достаточно велико. Осуществляемый разработчиком выбор из этого многообразия определяется не только свойствами объекта и предпочтениями разработчика, но и тем, насколько удобно с точки зрения последующего анализа в выбранной модели представляются рассматриваемые отказы. Если ставится задача автоматизации процедур разработки средств диагностирования, то на первый план выходит эффективность внутримашинного представления модели. При этом ее наглядность, важная для ручных методов, может пострадать. Рассмотрим сначала некоторые примеры моделей безынерционных устройств. Понятно, что любое реальное устройство инерционно, однако вполне может оказаться, что при диагностировании определенных отказов эта инерционность не существенна. Так обычно считают при диагностировании логических (комбинационных) схем. При этом при решении других задач в отношении логических схем могут применяться модели, учитывающие инерционность.

Начнем с одной из самых очевидных и привычных инженеру моделей логической (цифровой) схемы – структурной (рис. 4.5). На рисунке представлена простейшая логическая схема, реализующая функцию конъюнкции или логического умножения. Схема имеет два входа ии один выход, на которых формируются двоичные сигналы {0, 1}. Чаще всего, когда рассматривают вопросы диагностирования логических схем, отказы моделируют путем фиксации уровней сигналов на входах и выходах. Такую модель отказа называют константной. На рис. 4.5 предполагается, что в схеме отказал ее выход. Причем значение выхода всегда (тождественно) равняется нулю. Заметим, что при обсуждении этой модели мы неявно предполагали, что нам известна функция элемента. Безусловно, при использовании формальных алгоритмов синтеза средств диагностирования мы должны располагать библиотекой функций элементов.

На рис. 4.6 представлены два примера аналогового (а) и цифрового (б) функциональных преобразователей, реализующих в определенном смысле похожие функции соответственно:

и .

К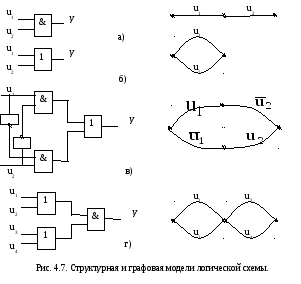аждый из преобразователей представляет собой комбинацию сумматоров и умножителя (аналоговых или цифровых). В этих выражениях скобками ограничены функции, отдельных элементов, что позволяет соотносить отказы в схеме с их отображением в формуле.

Упомянем для логического преобразователя еще одну, по-видимому, самую наглядную модель. Ее принято называть графовой. Она представлена на рис. 4.7. Заметим, что и машинное представление этой модели весьма компактно. Модель может рассматриваться как двухполюсный контактный эквивалент логической схемы. Полюса на рисунке отмечены зачерненными кружками. Любой путь между полюсами (последовательность ребер без повторений) соответствует входному набору (наборам), на котором логическая функция равна единице, любое сечение графа (набор ребер, разрывающий все пути между полюсами) соответствует входному набору (наборам), на котором логическая функция равна нулю. На рис. 4.7 приведены графовые модели для конъюнкции (а), дизъюнкции (б), исключающего ИЛИ (полусумматора) (в) и чуть более сложной логической схемы из трех элементов и с четырьмя входами (г). Видно, что конъюнкция представляется последовательными ребрами, дизъюнкция – параллельными, а схемы на рис. 4.7 в и г – композицией последовательных и параллельных подграфов.

Интересно проанализировать, как отображаются на графовой модели константные отказы (рис.4.8). Оказывается, то отказы типа () – тождественная единица – отображаются на графовой модели в виде короткого замыкания ребер, при котором соединяемые этим ребром вершины объединяются, а отказы типа () – тождественный нуль – в виде обрыва ребер.