Косоугольная фронтальная диметрия

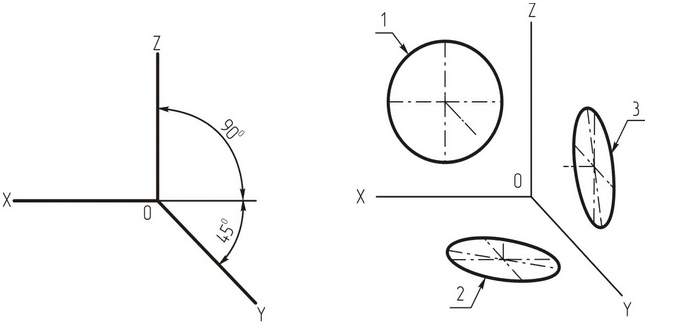
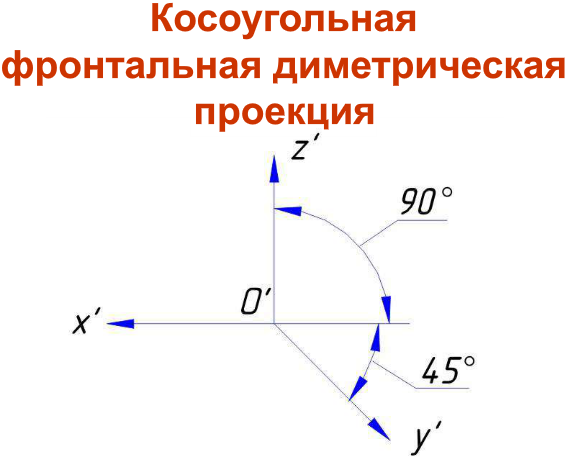
Положение аксонометрических осей в косоугольной фронтальной диметрической проекции приведено на рис. 6, а. Аксонометрические осиХиZсоставляют угол 90°, а осьУобразует угол 45° по отношению к горизонтальной линии. Этот угол допускается применять равный 30 или 60°.

Действительные коэффициенты искажения по осям Х и Z равны единице: u = w = 1; по оси У – вдвое меньше: v = 0,5. Соответственно линейные размеры предметов по оси У сокращаются в два раза.

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость в виде окружности. Окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, – в эллипсы (рис. 6, б).

6.Кривые Безье (https://learn.Javascript.Ru/bezier)

Кривая Безье задаётся опорными точками.

Их может быть две, три, четыре или больше. Например:

По двум точкам: По трём точкам: По четырём точкам:

Если вы посмотрите внимательно на эти кривые, то «на глазок» заметите:

1. Точки не всегда на кривой. Это совершенно нормально, как именно строится кривая мы рассмотрим чуть позже.

2. Степень кривой равна числу точек минус один. Для двух точек – это линейная кривая (т.е. прямая), для трёх точек – квадратическая кривая (парабола), для четырёх – кубическая.

3. Кривая всегда находится внутри выпуклой оболочки, образованной опорными точками:

 

Благодаря последнему свойству в компьютерной графике можно оптимизировать проверку пересечений двух кривых. Если их выпуклые оболочки не пересекаются, то и кривые тоже не пересекутся.

Основная ценность кривых Безье для рисования – в том, что, двигая точки, кривую можно менять, причём кривая при этом меняется интуитивно понятным образом.

У кривых Безье есть математическая формула.

Как мы увидим далее, для пользования кривыми Безье знать её нет особенной необходимости, но для полноты картины – вот она.

Координаты кривой описываются в зависимости от параметра t⋲[0,1]

• Для двух точек:

P = (1-t)P₁ + tP₂

• Для трёх точек:

P = (1−t)²P₁ + 2(1−t)tP₂ + t²P₃

• Для четырёх точек:

P = (1−t)³P₁ + 3(1−t)²tP₂ +3(1−t)t²P₃ + t³P₄

Вместо P_i нужно подставить координаты i-й опорной точки (x_i, y_i).

Эти уравнения векторные, то есть на для каждой из координат:

• x = (1−t)²x₁ + 2(1−t)tx₂ + t²x₃

• y = (1−t)²y₁ + 2(1−t)ty₂ + t²y₃

Вместо x₁, y₁, x₂, y₂, x₃, y₃ подставляются координаты трёх опорных точек, и в то время как t пробегает множество от 0 до 1, соответствующие значения (x, y) как раз и образуют кривую.

7.Кубический сплайн

Некоторая функция f(x) задана на отрезке , разбитом на части,.Кубическим сплайном дефекта 1 называетсяфункция , которая:

• на каждом отрезке 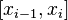являетсямногочленом степени не выше третьей;

• имеет непрерывные первую и вторую производные на всём отрезке ;

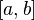• в точках 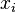выполняется равенство, т. е. сплайн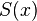интерполирует функцию f в точках .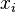

Для однозначного задания сплайна перечисленных условий недостаточно, для построения сплайна необходимо наложить какие-то дополнительные требования.

Естественным кубическим сплайном называется кубический сплайн, удовлетворяющий также граничным условиям вида:

Теорема: Для любой функции и любого разбиения отрезкасуществует ровно один естественный сплайн S(x), удовлетворяющий перечисленным выше условиям.

Эта теорема является следствием более общей теоремы Шёнберга-Уитни об условиях существования интерполяционного сплайна.

На каждом отрезке функцияесть полином третьей степени, коэффициенты которого надо определить. Запишем для удобствав виде:

тогда

Условия непрерывности всех производных до второго порядка включительно записываются в виде