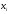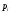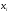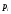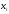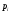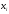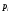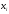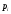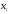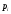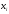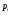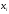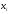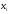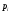Упражнения для выполнения

1. Монета подбрасывается 2 раза. Какая из таблиц представляет распределение дискретной случайной величины?

   хi 0 1 2 yi 1/4 1/4 1/2	хi 1 2 yi 1/2 1/4	хi 1 2 yi 1/2 1/2	хi 0 1 2 yi 1/4 1/2 1/4
   а	б	в	г

2. Какие значения вероятностей не достают в соответствующих законах распределения дискретной случайной величины.

   хi 1 4 5 7 yi 0,2 0,1 ___ 0,4	хi 1 4 5 7 yi 0,1 0,2 0,1 __	хi 1 4 5 7 yi __ 0,2 0,1 0,5
   а	б	в

3. Законами распределения дискретной случайной величины X могут являться соответствия …

а)	хi 1 3 4 yi 0,2 0,5 0,3	в)	хi -1 0 1 yi 0,8 0,1 0,1
б)	хi -1 1 3 yi 0,2 0,5 0,6	г)	хi 2 3 5 yi 0,2 0,1 0,3

В соответствие с последним номером вашей зачетной книжки выполните следующие задания:

4. Составьте закон распределения для дискретной случайной величины Х (таб.17).

Таблица 2

Вариант	Случайная величина
1	Случайная величина Xпредставляет собой выпавшие очки на костях домино. Всего костей – 28 штук.
2	Из партии, состоящей их 18 деталей, среди которых 4 бракованных, случайным образом выбраны 2 детали. Случайная величина представляет собой выбор среди двух деталей бракованной.
3	Случайная величина Xпредставляет собой выпавшие очки на двух игровых кубиках.
4	Эксперт оценивает качественный уровень трех видов изделий по потребительским признакам. Вероятность того, что изделию первого вида будет присвоен знак качества, равна 0,7; для изделия второго вида эта вероятность равна 0,9; а для изделия третьего вида 0,8. Случайной величиной Х является присвоение знака качества изделию.
5	Случайная величина Xпредставляет собой случаи выпадения герба при подбрасывании монеты 6 раз.
6	Первый стрелок при одном выстреле попадает в мишень с вероятностью 0,8, а второй стрелок – с вероятностью 0,6. Каждый сделал по одному выстрелу. Случайная величина Х– число попаданий в мишень.
7	В ящике находится 4 белых и 5 черных шаров. Из ящика вынимают 4 шара. Случайная величина Хпредставляет собой случаи появления белых шаров.
8	Стрельбу по цели ведут до получения двух попаданий. Вероятность попадания при одном выстреле равна 0,2.
9	Среди 10 патронов 4 боевых, а остальные – холостые. Наугад берут 3 патрона. Случайной величиной Х является число появления боевых патронов среди взятых.
10	Бросают три игральных кубика. Случайной величиной Х является появление четного числа очков.

5. Дан закон распределения дискретной случайной величины (таб.18)

Таблица 3

Вариант	Закон распределения дискретной случайной величины Х
1	1 2 4 8 0,3 0,1 0,2 0,4
2	2 3 4 5 0,5 0,2 0,1 0,2
3	2 4 8 10 0,1 0,5 0,1 0,3
4	1 2 5 10 13 0,1 0,3 0,2 0,3 0,1
5	-2 -1 0 1 2 0,1 0,2 0,3 0,3 0,1
6	1 3 4 6 7 0,1 0,1 0,3 0,4 0,1
7	5 7 10 15 0,2 0,5 0,2 0,1
8	100 150 200 250 300 0,4 0,3 0,2 0,05 0,05
9	490 90 10 0 -10 1/200 2/200 10/200 30/200 157/200
10	0 1 2 3 4 1/16 1/4 3/8 1/4 1/16

1. Постройте многоугольник распределения дискретной случайной величины.

2. Найдите математическое ожидание дискретной случайной величины.

3. Найдите дисперсию дискретной случайной величины.

4. Найдите среднее квадратическое отклонение дискретной случайной величины.

5. Найдите моду и медиану дискретной случайной величины.