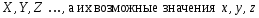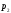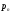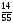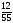Элементы математической статистики

Математическая статистика как наука начинается с работ знаменитого немецкого математика Карла Фридриха Гаусса, который на основе теории вероятностей исследовал и обосновал метод наименьших квадратов, созданный им в 1795 г. и примененный для обработки астрономических данных (с целью уточнения орбиты малой планеты Церера). Его именем часто называют одно из наиболее популярных распределений вероятностей – нормальное, а в теории случайных процессов основной объект изучения – гауссовские процессы.

Рональд Эйлмер Фишер (1890 - 1962) статист, генетик

Карл Пирсон (1857-1936) математик, статистик, биолог

В конце XIX в. – начале ХХ в. крупный вклад в математическую статистику внесли английские исследователи, прежде всего Карл Пирсон и Рональд Эйлмер Фишер. В частности, Пирсон разработал критерий «хи-квадрат» проверки статистических гипотез, а Фишер – дисперсионный анализ, теорию планирования эксперимента, метод максимального правдоподобия оценки параметров.

Ежи Нейман (1894-1977) математик, статистик

Андрей Николаевич Колмогоров (1903-1987) математик

В 30-е годы ХХ в. поляк Ежи Нейман вложил вклад в развитие общей теории проверки статистических гипотез, а советский математик академик Андрей Николаевич Колмогоров явился одним из основателем непараметрической статистики.

Математическая статистика бурно развивается и в настоящее время.

Случайная величина

Достаточно часто на практике рассматриваются такие испытания, в результате реализации которых случайным образом получается некоторое число. Например, при бросании игрального кубика выпадает число очков от 1 до 6, при взятии 6 карт из колоды можно получить от 0 до 4 тузов. За определенный промежуток времени (скажем, день или месяц) в городе регистрируется то или иное количество преступлений, происходит какое-то количество дорожно-транспортных происшествий. Из орудия производится выстрел. Дальность полета снаряда также принимает какое-либо значение случайным образом.

Во всех перечисленных испытаниях мы сталкиваемся с так называемыми случайными величинами.

Определение.

Случайная величина – это числовая величина, принимающая то или иное значение в результате реализации испытания случайным образом

Понятие случайной величины играет весьма важную роль в теории вероятностей. Если «классическая» теория вероятностей изучала главным образом случайные события, то современная теория вероятностей преимущественно имеет дело со случайными величинами.

Пример1.

1. количество очков, выпавших на верхней грани игрального кубика;

2. число тузов, при взятии из колоды 6 карт;

3. количество зарегистрированных преступлений за день или месяц;

4. число попаданий в мишень при четырех выстрелов из пистолета;

5. расстояние, которое пролетит снаряд при выстреле из орудия;

6. рост случайно взятого человека.

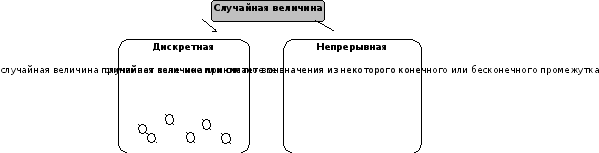
Рисунок 1. Виды случайных величин

Случайную величину можно задать:

• в виде таблицы (в которой указывается значение появления случайной величины и вероятности их появления), т.е. в виде ряда распределения случайнойвеличины (таб.16);

• графически, где в прямоугольной системе координат по оси Охоткладываются значения случайной величины, а по осиОу– соответствующие им вероятности. Полученные точки соединяются отрезками. Построенная таким образом фигура называется многоугольником распределения (рис.34).

Таблица 1. Пример ряда распределения случайной величины

		...
		…

Рисунок 2. Многоугольник распределения случайной величины

Пример2.

В ящике 4 белых и 8 черных шаров. Вынимаем три шара (без возвращения их в ящик). Случайной величиной Х является число появление белых шаров в выборке. Необходимо составить ряд распределения данной случайной величины и построить многоугольник распределения.

Решение.

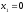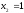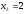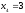Среди выбранных шаров может не оказаться белых шаров, т.е. , один белый шар, т.е., два белых шара, т.е., или все три шара будут белыми, т.е.. Найдем вероятности появления соответственных белых шаров.

Введем обозначения.

Событие А – первый шар белый, событие В – второй шар белый, С – третий шар белый, тогда:

;

.

.

.

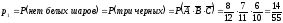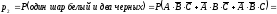
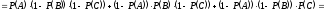
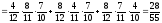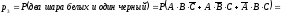
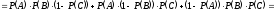
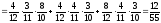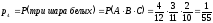Таким образом, закон распределения случайной величины Х имеет следующий вид:

х	0	1	2	3
p

Сделаем проверку: .

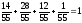Рисунок 3

Дискретная случайная величина имеет следующие числовые характеристики: