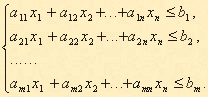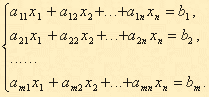1. Целевая функция.

Целевая функция – функция, переменные которой являются х1, х2, …, хn переменные модели, рассматриваемые экономико-математической моделью.

Целевая функция – это математическое представление зависимости критерия оптимальности от искомых переменных.

2. Градиент функции.

Вектор, компонентами которого служат значения частных производных, то есть вектор

называется градиентом функции , вычисленным в точке.

3. Общая задача линейного программирования.

Стандартная математическая формулировка общей задачи линейного программирования выглядит так: требуется найти экстремальное значение показателя эффективности (целевой функции)

(линейной функции элементов решения ) при линейных ограничительных условиях, накладываемых на элементы решения:

где - заданные числа.

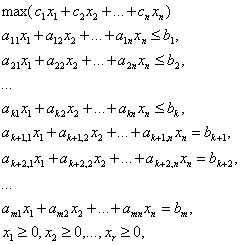
4. Стандартная задача лп.

В стандартной форме задача линейного программирования является задачей на максимум (минимум) линейной целевой функции. Система ограничений ее состоит из одних линейных неравенств типа « <= » или « >= ». Все переменные задачи неотрицательны.

Всякую задачу линейного программирования можно сформулировать в стандартной форме. Преобразование задачи на минимум в задачу на максимум, а также обеспечение не отрицательности переменных производится так же, как и раньше. Всякое равенство в системе ограничений равносильно системе взаимопротивоположных неравенств:

Существует и другие способы преобразования системы равенств в систему неравенств, т.е. всякую задачу линейного программирования можно сформулировать в стандартной форме.

2 вариант ответа:

Стандартная задача ЛП. 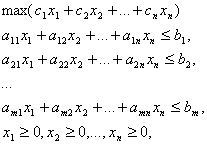или, в матричной записи,где— матрица коэффициентов. Векторназывается вектором коэффициентов линейной формы,— вектором ограничений.

5. Каноническая задача лп.

В канонической форме задача является задачей на максимум (минимум) некоторой линейной функции F, ее система ограничений состоит только из равенств (уравнений). При этом переменные задачи х₁, х₂, ..., х_nявляются неотрицательными:

К канонической форме можно преобразовать любую задачу линейного программирования.

Короткая запись канонической задачи ЛП:

Х=(х1, х2, …, хn), С=(с1, с2, …, сn).

2 вариант ответа:

Каноническая задача ЛП. 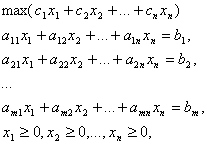или, в матричной записи,

6. Симметричные и несимметричные двойственные задачи.

Двойственная задача линейного программирования. Рассмотрим задачу ЛП 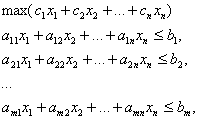(1) или, в матричной записи,(2) Задачей, двойственной к (1) (двойственной задачей), называется задача ЛП отпеременныхвида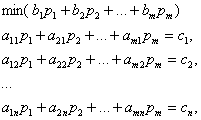(3) или, в матричной записи,(4) где. Правила построения задачи (3) по форме записи задачи (1) таковы: в задаче (3)

переменных столько же, сколько строк в матрицезадачи (1). Матрица ограничений в (3) — транспортированная матрица. Вектор правой части ограничений в (3) служит вектором коэффициентов максимизируемой линейной форме в (1), при этом знаки неравенств меняются на равенство. Наоборот, в качестве целевой функции в (3) выступает линейная форма, коэффициентами которой задаются вектором правой части ограничений задачи (1), при этом максимизация меняется на минимизацию. На двойственные переменныенакладывается условие неотрицательности. Задача (1), в отличии от двойственной задачи (3) называется прямой.Теорема двойственности. Если взаимодвойственные задачи (2), (4) допустимы, то они обе имеют решение и одинаковое значение.

Симметричные двойственные задачи

Разновидностью двойственных задач линейного, программирования являются двойственные симметричные задачи, в которых система ограничений как исходной, так и двойственной задач задается неравенствами, причем на двойственные переменные налагается условие неотрицательности.