Зависимые события. Вероятность произведения зависимых событий.

События A и B называются зависимыми, если вероятность одного из них зависит от того, произошло или не произошло другое событие.

Рассмотрим пример.

В коробке находится a белых и b черных шаров. По очереди один за другим извлекаются 2 шара и назад не возвращаются.

Обозначим случайные события:

A ‒ 1‒й шар белый;

B ‒ 2‒й шар белый.

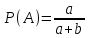
Если событие A не произошло, то вероятность события B:

Если событие A произошло, то есть первый шар белый, тогда

Определение. Вероятность события B, вычисленная при условии, что событие A произошло, называется условной вероятностью, и обозначается или

Для условной вероятности имеют место формулы:

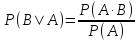
Теорема 4. Вероятность произведения зависимых событий равна произведению вероятности одного из них на условную вероятность другого события, вычисленную при условии, что первое событие произошло.

Теорема следует из предыдущих формул:

или

Распространим эту теорему на любое число зависимых событий:

Пример.

На складе 20 мешков с мукой высшего сорта. 12 мешков первого сорта. 5 мешков второго сорта. По очереди один за другим достают 3 мешка с мукой и назад не возвращают.

Найти вероятность того, что первый мешок с мукой высшего сорта (событие ), второй мешок с мукой первого сорта (событие), третий мешок с мукой второго сорта (событие).

Решение:

6.Основные формулы теории вероятностей. Формула полной вероятности.

Теорема 1.Вероятность события A, вычисленная при условии осуществления одного из несовместных событий H₁, H₂,H₃, …., H_n, образующих полную группу, находится по формуле:

‒ формула полной вероятности,

где события ‒ гипотезы.

Доказательство:

Так как событие A,может произойти только с одним из несовместных событий или или, или, то

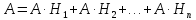
Тогда по теореме о вероятности произведения зависимых событий, получим:

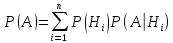
Пример 1.

Партия деталей изготавливается тремя рабочими. Причем первый рабочий изготовил 25% деталей. Второй 35% деталей. Третий 40% деталей. В продукции первого рабочего брак составляет 5%. У второго рабочего брак составляет 4%.У третьего рабочего брак составляет 2%. Случайно выбранная для контроля деталь оказалась бракованной. Найти, чей брак вероятнее всего.

Решение:

деталь изготовил первый рабочий.

деталь изготовил второй рабочий.

деталь изготовил третий рабочий.

A ‒ взятая деталь бракованная.

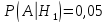
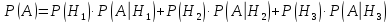
Формула Байеса.

Пусть событие A может произойти с одним из несовместимых событий образующих полную группу.

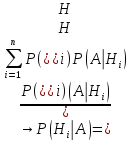
‒ формула Байеса.

Пример.

В торговую фирму поступили телевизоры от трех поставщиков в отношении 1:4:5. Телевизоры от первого, второго и третьего поставщиков не потребуют ремонта в течение гарантийного срока, в следующих 98%, 88% и 92% случаях.

Найти:

1. Вероятность того, что поступивший в торговую фирму телевизор не потребует ремонта в течение гарантийного срока (событие A).

2. Вероятность того, что проданный телевизор потребовал ремонта в течение гарантийного срока (событие B).

3. От какого поставщика вероятнее всего этот телевизор.

Решение:

телевизор поступил от i ‒ й фирмы, i= 1, 2, 3. Тогда

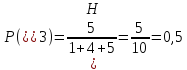
2.

Ответ: вероятнее всего брак второй фирмы, так как брак второй фирмы составил максимальную вероятность равную .