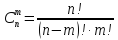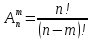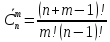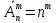Основные понятия комбинаторики.

n – факториал ‒ произведение первых n ‒ натуральных чисел (обозначается n!).

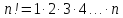
Основными понятиями комбинаторики являются ‒ размещения, перестановки и сочетания.

Определение 1. Пусть имеется множество, содержащее n ‒ элементов.

Размещением из n ‒ элементов по m ‒ элементов (m ≤ n) ‒ называются все подмножества, содержащие m ‒ элементов и отличающиеся друг от друга или составом своих элементов или порядком их следования.

‒ число размещений из n ‒ элементов по m ‒ элементов.

Определение 2. Перестановками из n ‒ элементов называются размещения из n ‒ элементов по n ‒ элементов.

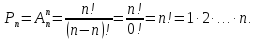
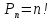–число перестановок из n ‒ элементов.

Определение 3. Сочетаниями из n ‒ элементов по m ‒ элементов (m≤n) называются все m‒ элементные подмножества n ‒ элементного множества, отличающиеся друг от друга только составом своих элементов.

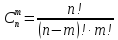
‒ число сочетаний из n ‒ элементов по m ‒ элементов.

Свойства сочетаний:

1.

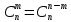
Доказательство:

Так как

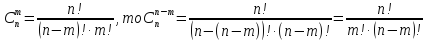
Следовательно,

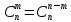
Примеры:

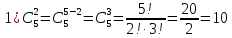
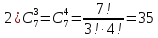
2.

Доказательство:

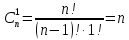
Примеры:

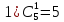
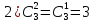
3.

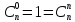
Доказательство:

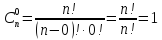
Примеры:

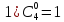
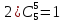
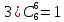
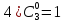
Бином Ньютона и его свойства.

Воспользуемся формулами:

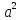=+2ab+=+

==

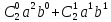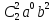
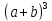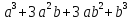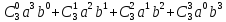
Используя принцип математической индукции (от частных примеров к общей формуле), получим формулу Ньютона:

=

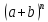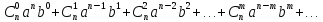
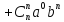
Или кратко:

– формула Ньютона для степени бинома или бином Ньютона.

Свойства:

1. Формула содержит (n+1) ‒ слагаемое.

2. Показатель степени a ‒ убывает от n до 0; Показатель степени b – возрастает от 0 до n.

3. Любой член разложения можно найти по формуле:

.

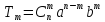4. Коэффициенты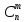называются – биноминальными. Биноминальные коэффициенты, равноудаленные от концов разложения, равны между собой.

5. Сумма всех биноминальных коэффициентов находятся по формуле:

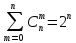
Доказательство:

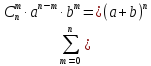
Пусть a = b = 1.

Тогда

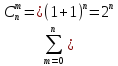
Примеры на формулу Ньютона и ее свойства:

Пример 1.

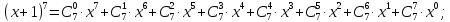
Где

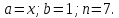
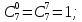
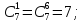
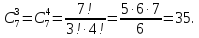
Следовательно,

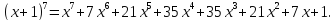
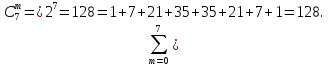
Пример 2.

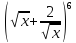
Найти: .

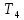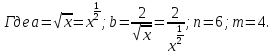
Решение:

В комбинаторных задачах удобно пользоваться следующей таблицей:

Выбор	Сочетания	Размещения	Перестановки
Без повторения
С повторением

2.Понятие случайного события. Виды случайных событий.

Случайным событием, связанным с некоторым опытом (испытанием) называется всякое событие, которое при осуществлении опыта может произойти, а может и не произойти.

Случайные события обозначаются, заглавными буквами латинского алфавита A,B,C….

Виды случайных событий:

1. Событие, которое всегда происходит в результате опыта, называется достоверным. Обозначается .

2. Событие, которое никогда не происходит в результате опыта, называется – невозможным. Обозначается .

3. Событие, состоящее в том, чтобы событие A не произошло называется противоположным событию А. Обозначается .

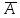4. События A и B называются несовместными, если они не могут произойти одновременно.

5. События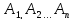называютпопарно несовместными, если никакие два из них не могут произойти одновременно.

6. События 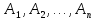образуютполную группу событий, если в результате опыта непременно произойдет, хотя бы одно из них.

7. События A и B называются равновероятными, если в результате опыта нет оснований считать одно из них более возможным, чем другое.

8. Событие, приводящее к наступлению события A, называется благоприятствующим событию А.

9. События 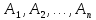, образующие полную группу попарно несовместных равновероятных событий, называютсяэлементарными событиями.