Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

speckurs

.pdf

Скачиваний:

Добавлен:

19.03.2016

Размер:

267.64 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Из (1.58) следует, что через точки перевала z0 = ±i проходит гипербола,

определяемая уравнением x2 − y2 + 1 = 0. Если изменить контур ин-

тегрирования таким образом, чтобы он совпал с указанной гиперболой, то мнимая часть фазовой функции не изменяется вдоль всего пути интегрирования. Деформация начального пути интегрирования возможна только в том случае, если функция eλS(z) экспоненциально мала на дугах бесконечного радиуса, соединяющих точку действительной оси с точкой на гиперболе. Условие экспоненциальной малости eλS(z) эквивалентно тому, что ReS(z) < 0, а как следует из (1.58), такое возможно только, если дуги лежат в первой и второй четвертях. Таким образом, мы можем деформировать контур только таким образом, чтобы он прошел через точку z0 = i. Тогда имеем: S(z0) = −2/3, S′′(z0) = −2, θ = π, φ = 0. Используя (1.55), получим:

Ai(z) ≈	1	(−	2	(1.59)
	2 π√z exp		3 z3/2) .
	√

1.9.Задачи для самостоятельной работы

1.Используя метод перевала найти асимптотику функции Бесселя (см. (1.44)) для z n.

Ответ: Jn(z) ≈ (

)

nn√

, n z.

2πn

2. Найти асимптотику для следующего интеграла при λ → ∞:

∞

λ2

J(λ) =

√

∫0

exp [i

− iϵt] t−3/2dt,

(1.60)

4πi

если ϵ > 0.

√

e− 2ϵλ

Ответ: J(λ) ≈

3. Найти асимптотику для следующего интеграла при λ → ∞:

(1.61)

J±(λ) =

∫0

[exp

(−t3 ± λt) + sin (t3 ± λt)] dt.

∞

Ответ: J−(λ) ≈

+ √

√

sin (−

λ3/2 +

);

J+(λ) ≈

−

√

exp (

λ3/2).

Глава 2.

Отрицательный ион в постоянных электрическом и магнитном полях

Хорошо известно, что круг задач, решаемых аналитически в квантовой механике, весьма ограничен и поэтому учет дополнительного взаимодействия с электрическим или магнитным полем, как правило, выполняется с помощью стандартного аппарата теории возмущений. В большинстве случаев, точность результатов, полученных пертурбативными методами, является достаточной для описания спектров атомов или ионов в магнитных и электрических полях. Тем не менее, существует ряд трехмерных моделей позволяющих решить задачу без каких-либо ограничений на напряженность статических полей. Одной из таких моделей является модель потенциала нулевого радиуса [3], наиболее часто использующаяся для описания слабосвязанных систем, таких, как например, отрицательные ионы.

2.1.Метод потенциала нулевого радиуса

Рассмотрим слабосвязанную систему, взаимодействующую со статическим полем, описываемым потенциалом V (r). Взаимодействие слабосвязанного электрона с атомным остовом, будем описывать с помощью потенциала нулевого радиуса (δ-потенциала):

	2π~2		∂		(2.1)
U(r) =		δ(r)		r,
	{m
		∂r

где δ(r) – функция Дирака, {– некоторая постоянная. Из определения δ-потенциала следует, что волновая функция при r → 0 имеет вид:

( )

r 0	0	1	− {		(2.2)
r 0	0	r	− {		(2.2)
lim ψ(r) = f				,

→

где f0 — некоторая константа. Действительно, запишем уравнение Шредингера:

(−	~2
(−	2m 2 − E0) ψ(r) = −U(r) ψ(r),	(2.3)

где V (r) ≡ 0 и U(r) определяется (2.1). Для r ≠ 0 решение (2.3) для связанного состояния с нулевым орбитальным моментом имеет вид:

ψ(r) = N	exp (−√			r)	.
		−	2mE0
			~2			(2.4)

	r

Рассмотрим поведение волновой функции в окрестности точки r = 0, где членом E0ψ(r) можно пренебречь. Подставляя (2.4) при малых r в уравнение (2.3) имеем:

2mE0

2π~2

∂ 1

2mE0

−

(

−

√

−

) = −

δ(r)

(

−

√

−

) .

(2.5)

∂r

Учитывая, что

= −4πδ(r),

(2.6)

получим:

~2{2

e−{r

E0 =

−

, ψ(r) = N

(2.7)

откуда и следует (2.2). Отметим, что граничное условие (2.2) не изменяется, даже если на систему действуют другие силы, потенциал которых ограничен при r = 0. Тогда с учетом (2.2) действие δ-потенциала на волновую функцию можно записать в виде:

U(r)ψ(r) = −	2π~2	(2.8)
	m f0δ(r).

Рассмотрим уравнение Шредингера для слабосвязанного электрона, находящегося под действием двух статических потенциалов U(r) и V (r):

(−	~2
(−	2m 2 + U(r) + V (r)) ψ(r) = Eψ(r).	(2.9)

Уравнение на собственные функции и значения (2.9), можно записать в виде: ∫

ψ(r) = − dr′ GE(r, r′) U(r′) ψ(r′), (2.10)

где GE(r′, r) функция Грина свободной частицы, двигающейся в потенциале V (r):

[H0 (r) − E] GE(r, r′) =

	24
(−	~2
(−	2m 2 + V (r) − E) GE(r, r′) = δ(r − r′). (2.11)

Выразим GE(r, r′), через нестационарную, запаздывающую Грина G(r, t; r′, t′)1:

∫

GE(r, r′) = − G(r, t; r′, t′) e ~i E(t−t′ ) dt′,

где G(r, t; r′, t′) удовлетворяет уравнению:

()

i~∂t∂ − H0(r) G(r, t; r′, t′) = δ(r − r′) δ(t − t′).

Используя (2.14) и (2.8), запишем (2.10) в виде:

∫∫

функцию

(2.14)

(2.15)

ψ(r) = dt′ dr′G(r, t; r′, t′) U(r′) ψ(r) e				i	E(t−t′ ) =
				~
	2π~2		∫			i
−		f0		dt′G(r, t; 0, t′) e			E(t−t′ ).	(2.16)
						~
	m

Исследуем поведение волновой функции (2.16) при малых r. Для этого

прибавим и отнимем из (2.16) интеграл:

−

2π~2

∫ G0(r, t; 0, t′)eiE(t−t′ )/~dt′ =

exp i

mr2

+ i E (t

−

t′)

√

exp

r ,

(

−

3/2

) dt′ =

−

√

∫

(t t′ )

(−

2mE

)

2πi~

(t − t′)

−∞

(2.17)

1Соотношение (2.14) может быть проверено используя спектральное разложение для функции Грина G(r, t; r′, t′):

G(r, t; r′, t′) = −i (t − t′) ∫ dλ φ (r′) φ (r) e− ~i E (t−t′ ), (2.12)

где (x) – функция Хевисайда, φ (r) и E собственная функция и собственное значе-

ние оператора H0(r) соответственно, λ – набор квантовых чисел. Подставляя

(2.12)

(2.14) получим:

− ∫

G(r, t; r′, t′) e

E(t−t′ ) dt′ =

∫

dt′ (t − t′) ∫

dλφ (r′)φ (r)e

(E−E )(t−t′ ) =

∫

dλ

φ (r′)φ (r)

= G(r, r′),

(2.13)

E − E − i0

где для интегрирования по t′ мы использовали замену E − E → E − E + i0, позволяющую регуляризовать интеграл при t′ = −∞.

где G0(r, t; 0, t′) нестационарная функция Грина свободной частицы:

3/2

m(r r )2

Θ(t − t′) (

)

exp (i

) .

G0(r, t; r′, t′) =

−

− ′

(2.18)

2πi~(t

−

t′)

2~(t t′)

−

Тогда для волновой функции (2.16) при r → 0 имеем:

√

−2mE

ψ(r) =

−

2π~2

{G(0, t; 0, t′) − G0(0, t; 0, t′)} e

f0 ∫

E(t−t′ )dt′.

(2.19)

Сравнивая (2.19) с граничным условием (2.2), получим искомое уравнение на энергию E в модели потенциала нулевого радиуса:

√			2π~2	∫ {G(0, t; 0, t′) − G0(0, t; 0, t′)} e
	2mE				i
	−	− { = −				E(t−t′ )dt′. (2.20)
					~
	~		m

Следует отметить, что интеграл в правой части (2.20) не зависит от t. Действительно, ввиду стационарности задачи, времена t и t′ должны входить

вфункцию Грина только в виде комбинации t−t′, тогда подынтегральная функция в (2.20) зависит только от t − t′, а следовательно интеграл не зависит от t. Более того, интеграл в (2.20) — сходящийся. Действительно,

вточке t′ t, функция Грина ведет себя как 1/(t−t′)3/2, однако, такой тип сингулярности подынтегральной функции пропадает из-за разности двух функций Грина, поэтому подынтегральная функция может иметь сингулярность вида 1/(t − t′)1/2, которая, очевидно, является интегрируемой.

2.2.Отрицательный ион в постоянном электрическом поле

Нестационарная функция Грина для потенциала V (r) = |e|zF может быть представлена в виде [4]:

Θ(t − t′) (

)

3/2

G(r, t; r′, t′) = −

eiS(r,t;r′ ,t′ )/~,

(2.21)

2πi~(t − t′)

где

S(r, t; r′, t′) =

m(r − r′)2

−

|e|

F (z + z′)(t

−

t′)

−

e2F 2(t − t′)3

(2.22)

2(t − t′)

24m

Подставляя явный вид функции Грина (2.21) в (2.20) и после элементарных преобразований получим2:

∞ exp

Eτ

e2F 2τ3

(

24m

) −

{ =

−

dτ,

(2.23)

−

√2π~i

∫0

3/2

или, вводя безразмерные величины ϵ = E/|E0|, F = F/F0, ξ =

τ|E~

, где

√

F0 =

2m|E0|3

|e|~

(

)

i F2

∞ exp

iϵξ

−

ξ3

−

∫0

(2.24)

−1 =

√

dξ.

ξ3/2

4πi

Исследуем уравнение (2.24) для двух предельных случаев F 1 и F 1.

2.2.1.Случай F 1

Будем полагать, что в интеграле (2.24) ϵ — отрицательный параметр,

√

тогда после замены переменной ξ = 2 −ϵz/F, перепишем уравнение (2.24) в виде:

−

√8πi√ ϵ

∫

[

z3/(

)]

∞

2(−ϵ)3=2

1 =

exp −i

z +

− 1

dz.

(2.25)

−

Так как F 1, то параметр λ = 2(−ϵ)3/2/F большой и интеграл можно

вычислить, используя метод перевала. В данном случае фазовая функция

( )

определяется соотношением S(z) = −i z + z3 и с точностью до знака

совпадает с фазовой функцией интеграла (1.56). Тогда, анализ поведения функции S(z) аналогичен тому, что был представлен в параграфе (1.8.1.). В результате такого анализа, мы имеем: (i) z1,2 = ±i являются перевальными точками для функции S(z); (ii) линии наискорейшего спуска

задаются уравнением x2 − y2 + 1 = 0; (iii) функция eλS(z) экспоненци-

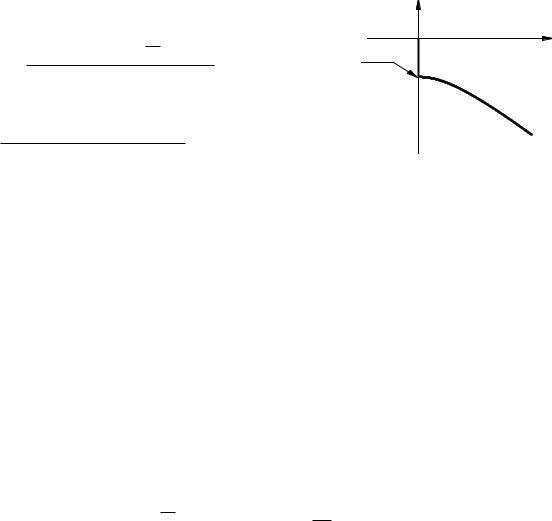
ально мала на дуге бесконечного радиуса, лежащей в третей и четвертой четвертях, соединяющей точки гиперболы с точками действительной оси. Пункты (i)–(iii) позволяют деформировать контур интегрирования таким образом, чтобы он представлял собой отрезок мнимой оси, проходящий

2В параграфе используются результаты полученные в [5]-[7] .

через точки (0, 0) и z2, и гиперболу x2 −y2 + 1 = 0, лежащую в четвертом

квадранте (см. рис. 2.1). Тогда интеграл (2.25) можно записать в виде:

[−iλ (

3 )] −

dz =

3/2

∫0

∞ exp

z + z3

[−

(

)] −

dz +

exp [−iλ (

)] −

dz, (2.26)

∫0

3/2

z2 exp

iλ

z + z3

− y2 + 1 = 0.

где кривая T определяется гиперболой x3

Рассмотрим первый интеграл в пра-

вой части (2.26):

Im z

exp [−iλ (

)] −

J1 =

∫0

3/2

dz =

z=-i

Re z

z + z

∫0

1/2

exp

−λ

x − x3

− 1

(2.27)

[

( 3/2

)]

dx.

Проинтегрируем (2.27) один раз по ча-

Рис. 2.1.

стям:

										∞			e−λ(x−	x3	)
		1/2			32 λ				1/2				e−λ(x−	3	)		2
	J1 = 2i		(		32 λ	)							x1/2			(		)
			(			)				0						(		)
				1 − e− −2i λ ∫													1 − x dx ≈
							3	)
2i	1/2	1/2		∞ e−λ(x−x3				)	(		2	)
			0						(			)
		− 2i λ ∫			x1/2				1 − x dx,

где мы пренебрегаем экспоненциально малой величиной e−23 λ на фоне единицы.

Видно, что основной вклад в интеграл дает точка x = 0, тогда раскладывая экспоненту в ряд:

e−λ(x−x33 ) ≈ e−λx (1 + λx3 + · · · ) , 3

и применяя метод Лапласа (см. параграф 1.5.), получим:

J1	≈ 2 i1/2 − 2√iπλ		(1 − 8λ2 ) .
			1

(2.28)

(2.29)

Интеграл по контуру T можно вычислить, используя метод перевала. Используя формулу (1.55), где z0 ≡ z2, и S(z0) = −23 λ, S′′(z0) = −2, получим:

[−iλ

(

3/2

)]

−

2i1/2 + e−3

π i3/2

, (2.30)

exp

z +

∫

≈ −

√

где фактор «1/2» в последнем члене возникает из-за того, что интегрирование ведется от точки перевала. Тогда, для интеграла (2.26) имеем оценку:

[−iλ

(

)] −

2√

e−3

√

i3/2

, (2.31)

dz =

iπλ

∫0

3/2

−

8λ

(

)

∞ exp

z + z3

и уравнение (2.25) можно записать в виде:

( ϵ)3/2

1 = √−ϵ (1

) − i

(−

) .

−

exp

−

(2.32)

( ϵ)3

8( ϵ)

−

Уравнение (2.32) можно решить методом последовательных приближений. Для этого перенесем в левую часть все члены, явно независящие от F, а в оставшихся членах положим ϵ = −1:

√

exp

(−

(2.33)

ϵ =

−

32 −

3F )

√

Полагая, что ϵ = −1 + ∆, где ∆ маленькая поправка, т.е. 1 − −ϵ ≈ ∆2 , получим из (2.33)

∆ =		F2	i	F	exp	(−	4	.	(2.34)
	−	16 −
			4				3F )

Реальная часть ∆ определяет сдвиг уровня (эффект Штарка) в электрическом поле, а мнимая часть (2Im∆) дает ширину (вероятность распада в единицу времени) атомного уровня.

2.2.2. Случай F 1

В этом случае параметр λ = 2(−ϵ)3/2/F нельзя считать большим, более того, как мы увидим ниже, мнимая часть ϵ уже сравнима с действительной, поэтому интеграл в (2.24) понимается в смысле аналитического

продолжения по ϵ. Сделаем замену переменной ξ = x/F2/3 в интеграле (2.24), тогда уравнение на энергию можно записать в виде:

()

∞ exp

iεx − i x12 − 1

−

√

∫0

dx, ε =

(2.35)

F1/3

x3/2

F2/3

4πi

Если F 1, то левую сторону уравнения (2.35) можно рассматривать как малое возмущение к правой части, тогда ϵ может быть представлено в виде ряда по степеням F−1/3:

ε = ξ0 + ξ1F−1/3 + ξ2F−2/3 · · · ,

(2.36)

или для ϵ имеем:

ϵ = ξ0F2/3 + ξ1F1/3 + ξ2 + · · · .

(2.37)

Значение коэффициентов ξn (n = 0, 1, 2, ...) можно получить только численно, например, ξ0 = 0.44e−iπ/3, ξ1 = −0.86e−iπ/6.

2.3.Отрицательный ион в постоянном магнитном поле

Рассмотрим сдвиг слабосвязанного уровня под действием постоянного магнитного поля. В этом случае потенциал V (r) можно представить в виде:

V (r) =		\|e\|	HLˆ		+	e2	[H	×	r]2,	(2.38)
	2mc			z		8mc2

где H — напряженность		магнитного поля,							ˆ	— оператор z-
									Lz

проекции орбитального момента. Функция Грина G(0, t; 0, t′) в этом

случае, отличается от G0(0, t; 0, t′)

только

дополнительным

фактором

ω(t−t′ )

−1

|e|H

sin

− i0

, где ω =

– ларморова частота [4]. Тогда,

используя[ ((2.20), для )]получим следующее уравнение

√

∫

{

}

− { = √

[

(

)]

2mE

~i Eτ

ωτ

∞

−

sin

− i0

−

− 1

dτ. (2.39)

2π~i

τ3/2

3В параграфе используются результаты, полученные в [8].

4π

x3/2

Будем использовать безразмерные величины введенные в параграфе 2.2.,

и обозначим Ω = H/H0

где H0 = |mce|~ |E0| (для большинства атомных

систем H0 108 − 109 Э), тогда (2.39) перепишем в виде:

∫0

[

(

)]

∞

eiϵξ

Ωξ

−

√−ϵ

− 1 =

√

ξ3/2

{

sin

− i0

− 1} dξ.

(2.40)

4πi

(

)

Инфинитезимальная поправка в sin

обходятся снизу.

	Ωξ	указывает на то, что полюса
	2	указывает на то, что полюса
	2

2.3.1.Случай слабого магнитного поля, Ω 1

Сделаем замену переменной z = Ωξ, тогда (2.40) примет вид:

∞

e−iεz

[

(

)]

Ω

√−ϵ − 1 = √

∫

{

sin

− i0

−

− 1} dz,

(2.41)

4πi

z3/2

где ε = −Ωϵ . Так как Ω 1 и ϵ < 0, то ε 1 и подынтегральная функция является быстроосциллирующей функцией. Однако, контур интегрирования может быть деформирован таким образом, чтобы подынтегральная функция вдоль нового контура стала быстрозатухающей функцией. Действительно, подынтегральная функция не имеет особых точек и полюсов в четвертом квадранте комплексной полуплоскости и экспоненциально мала на дуге бесконечного радиуса соединяющей точки действительной оси с точками мнимой оси (Im z < 0). Тогда контур интегрирования может быть деформирован в прямую линию, проходящую через точки (0, 0) и (0, −i∞). Изменяя путь интегрирования и делая замену z = −ix, получим:

∞

εx

√−ϵ − 1 = √

{

[sh

(

2 )]−

− 1} dx.

(2.42)

Ω ∫ e−

Раскладывая x2 [sh (x2 )]−1 − 1 в ряд по x (ограничиваясь первым неисчезающим членом) и используя метод Лапласа, получим:

√			Ω2		(2.43)
	−ϵ − 1	≈ −
				.
			96(−ϵ)3/2

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.11.2019142.34 Кб3SITUATsIONN_E_ZADAChI_-_LOR_BOLEZNI.doc
#
21.05.2015491.17 Кб31smagina-belousova-method.pdf
#
21.05.20151.16 Mб21Sorokin.pdf
#
22.11.201830.11 Кб6sotsiologia(2).docx
#
21.05.2015485.86 Кб10sotsiologia.rtf
#
19.03.2016267.64 Кб12speckurs.pdf
#
21.05.20155.14 Mб156spez_fiz_pr_zachita.pdf
#
20.05.2015137.2 Кб85SPSE2014.docx
#
21.05.2015917.91 Кб34SQL в вопросах и задачах.pdf
#
21.05.20155.12 Mб12srrf2014web.pdf
#
20.05.2015318.46 Кб8strany_i_stolitsy_blank_dlya_studentov.doc