
speckurs
.pdf
11
1.5.Метод Лапласа
1.5.1.Метод Лапласа
Пусть задан интеграл вида: |
|
∫b |
|
J(λ) = f(t)e−λS(t), |
(1.21) |
t0 |
|
где мы полагаем, что параметр λ большой и положительный. Наконец, пусть внутри отрезка [t0, b], S(t) > S(t0), а в окрестности точки t = t0 функции f(t) и S(t) имеют разложения:
λS(t) |
|
|
- |
|
|
f(t)e |
|
|
a |
t0 |
b |
Рис. 1.1. |
|
|
f(t) ≈ P (t−t0)(ν−1), S(t) ≈ S(t0)+Q(t−t0)µ,
где P и Q некоторые постоянные. Очевидно, основной вклад в интеграл дает область окрестности точки t0, где подынтегральная функция имеет резкий максимум (см. рис. 1.1). Тогда имеем:
J(λ) ≈ P e−λS(t0) ∫b (t − t0)ν−1e−λQ(t−t0) dt, |
(1.22) |
t0 |
|
Заменяя верхний предел b на «бесконечность» (так как, окрестность точки b вклада не дает), производя замену переменной ξ = −λQ(t − t0)µ, и используя интегральное выражение для Γ-функции (см. приложение), получим:
|
P e−λS(t0) |
|
ν |
|
||
J(λ) ≈ |
|
Γ |
( |
|
) . |
(1.23) |
(λQ)ν/µ µ |
µ |
|||||
Приведем явный вид формулы (1.23) для наиболее часто встречающихся случаев ν = 1 и µ = 1, 2:
J(λ) ≈ |
P e−λS(t0) |
J(λ) ≈ P e−λS(t0)√ |
2π |
(1.24) |
||
|
, |
|
. |
|||
λS′(t0) |
λS′′(t0) |
|||||
Сделаем несколько замечаний относительно применения метода Лапласа:
1.Если отрезок интегрирования функции от a до b включает точку t0 (см. рис. 1.1), то, очевидно, приближенное значение интеграла (1.23) должно быть удвоено;

12
2.Если отрезок интегрирования функции содержит внутри себя i точек, аналогичных точке t0, то приближенное значение интеграла определяется соответствующей суммой вкладов от каждой точки.
Пример 1. Исследуем асимптотическое поведение Γ-функции при больших значениях аргумента. Запишем интегральное представление Γ- функции (А.1) в виде:
∞ |
∞ |
|
|
Γ(z) = ∫0 |
ez ln(ξ)−ξdξ = zz ∫0 |
e−z(t−ln(t))dt. |
(1.25) |
В интеграле (1.25) имеем: f(t) ≡ 1, S(t) = t − ln(t), λ = z. В этом случае, минимальное значение S(t) достигается в точке t0 = 1 (S′(t0) = 0), откуда используя (1.23) для µ = 2, ν = 1, и полагая P = 1, Q = 1/2, получаем:
|
zze |
|
z |
Γ ( |
1 |
|
|
|
|
|
|
Γ(z) ≈ |
− |
|
√2πzz−1/2e−z. |
(1.26) |
|||||||
|
|
|
2 ) = |
||||||||
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z/2
Отметим, так как точка t0 = 1 лежит внутри области интегрирования, то результат, полученный с использованием соотношения (1.23), был удвоен. Соотношение (1.26) называется формулой Стирлинга и имеет высокую точность даже при малых z, например, при z = 1, формула Стирлинга дает значение 0.922, что близко к точному значению 1.
Пример 2. Исследуем поведение модифицированной функции Бесселя при больших значениях аргумента z (z n):
|
|
π |
|
|
In(z) = |
1 |
∫0 |
ez cos t cos(nt) dt. |
(1.27) |
π |
В этом случае f(t) = cos(nt) и S(t) = − cos(t). Минимальное значение функция S(t) принимает в точке t0 = 0, где
f(t0) = 1, S(t) ≈ −1 + (t)2/2, |
|
|||
откуда с учетом (1.23) имеем: |
|
|||
|
ez |
(1.28) |
||
In(z) ≈ |
√ |
|
. |
|
2πz |
||||
Пример 3. Найдем первый член асимптотического разложения полинома Лежандра при x > 1 и n 1. Полином Лежандра порядка n может

13
быть представлен в виде интеграла2:
|
|
|
|
π |
( √ |
) |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||
|
|
|
1 |
∫ |
|
|
|
n |
|
(1.29) |
|||
|
|
Pn(x) = |
π |
x + |
x2 − 1 cos(t) |
|
dt. |
||||||
В данном примере λ = n, f(t) ≡ 1, и S(t) = − ln |
x + √ |
|
cos(t) . |
||||||||||
x2 − 1 |
|||||||||||||
Функция |
S(t) |
принимает минимальное значение при |
t = 0 |
. Отметим, |
что |
||||||||
|
( |
) |
|||||||||||
в точке t = π первая производная также обращается в нуль, однако в этой точке значение функции S(t) максимально, следовательно, вклад от окрестности этой точки в интеграл минимален по сравнению с окрестностью точки t = 0, и поэтому вкладом от этой точки можно пренебречь. Вычисляя вторую производную от S(t) с учетом (1.23), получим:
|
|
(x + √ |
|
|
|
|
||
P |
(x) |
x2 − 1)n+1/2 |
. |
(1.30) |
||||
|
|
|||||||
|
|
|
|
|||||
n |
|
≈ √2πn(x2 − 1)1/4 |
||||||
1.5.2.Оценка интегралов от быстро осциллирующих функций
В ряде случаев, метод Лапласа может быть использован для оценки |
|||||
интегралов от быстро осциллирующих функций. Очевидно, такое воз- |
|||||
можно, если контур интегрирования можно изменить таким образом, |
|||||
чтобы вдоль нового контура интегрирования подынтегральная функция |
|||||
экспоненциально затухала. Продемонстрируем этот прием на следующем |
|||||
примере. |
|
|
|
|
|
Требуется оценить интеграл вида: |
|
y |
|||
∞ |
eiωt |
|
|
|
|
J(ω) = ∫ |
√1 + t2 |
dt, |
(1.31) |
C1 |
C2 |
−∞ |
|
|
|
|
C4 C3 |
для ω 1. Подынтегральная функция |
|
|
|||
экспоненциально |
затухает вдоль |
поло- |
|
z=i |
|
жительной мнимой оси, поэтому изме- |
|
C5 |
|||
|
x |
||||
ним контур интегрирования таким об- |
|
||||
|
|
||||
разом, чтобы он прошел вдоль положи- |
|
Рис. 1.2. |
|||
тельной мнимой оси. Так как подынте- |
|
|
|||
гральная функция содержит точку ветвления при t = i, то деформиру- |
|||||
ем контур таким образом, чтобы новый контур интегрирования обходил |
|||||
точку ветвления, а именно новый контур интегрирования состоит (см. |
|||||
рис. 1.2) из двух дуг бесконечного радиуса C1 и C2, петли бесконечно |
|||||
2Данный пример имеет чисто академический интерес, поскольку стандартизован- |
|||||
ная область определения полиномов Лежандра, в том числе используемая в задачах |
|||||
квантовой механики, соответствует |x| ≤ 1. |
|
|
|||

14
малого радиуса C5 вокруг точки ветвления, и вертикальных линий C3 и C4. В силу теоремы Коши имеем:
∫∞ · · · dt = ∫C1 |
+ ∫C2 |
+ ∫C3 |
+ ∫C4 |
+ ∫C5 . |
(1.32) |
−∞ |
|
|
|
|
|
Так как подынтегральная функция экспоненциально затухает в верхней комплексной полуплоскости, то интеграл по бесконечным дугам C1 и C2 равен нулю. Интеграл по петле C5 так же равен нулю. Действительно, если t = ρeiφ, где ρ радиус петли, то для интеграла вдоль C5 имеем следующую оценку:
∫ |
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
iωt |
|
|
2π |
exp |
iω(ρeiφ + i) |
iρeiφ |
|
|
|
|
||
|
|
|
|
|
|
0 |
√ |
|
|
|
|
|
|
||
C5 |
√1 + t |
|
|
|
[ |
|
1 + (i + ρei |
]) |
|
|
|
|
|
||
|
|
e |
|
|
dt = |
|
|
|
|
|
dφ |
√ |
ρ. |
(1.33) |
|
|
|
|
|
2 |
|
|
|
|
|
φ 2 |
|
|
|
|
|
Устремляя радиус петли к нулю, получаем, что интеграл вдоль контура C5 равен нулю. Интегралы вдоль линий C3 и C4 равны между собой. Действительно, так как контуры C3 и C4 связаны петлей C5 вокруг точки ветвления, то при переходе с C3 на C4 подынтегральная функция меняет знак на обратный, но с учетом того, что направления интегрирования вдоль C3 и C4 противоположны, получаем равенство интегралов вдоль линий C3 и C4. В итоге получаем:
∞ |
|
eiωt |
|
|
|
eiωz |
|
∞ |
e−ωξ |
|
|
|
||
∫ |
√ |
dt = 2 |
∫C4 |
√ |
dz = 2 |
∫ |
|
dξ. |
(1.34) |
|||||
|
|
|
|
|
|
|||||||||
1 + t2 |
1 + z2 |
|
ξ2 |
− |
1 |
|||||||||
−∞ |
|
|
|
|
|
|
|
1 |
√ |
|
|
|
||
Интеграл (1.34) можно приближенно вычислить с помощью метода Ла-
√
пласа для ω 1, где t0 = 1, S(t0) = 1, µ = 1, ν = 1/2, P = 1/ 2. В результате использования (1.23), получим:
√
J(ω) ≈ |
2π |
e−ω. |
(1.35) |
ω |
1.6.Задачи для самостоятельной работы
1. Получить первый член асимптотического разложения интеграла
∞ exp −t − αt |
|
|
|
J(α) = ∫ |
[t3/2 |
] |
dt, |
0
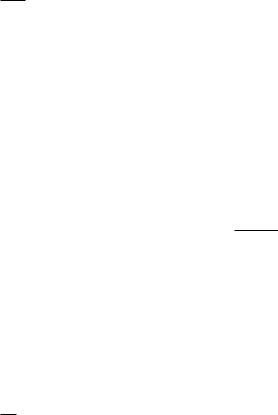
15
для α 1. |
√ |
|
|
e−2√α. |
|
Ответ: J(α) = |
|
α |
|||
|
|
|
π |
|
|
2. Получить первый член асимптотического разложения интеграла
π/2 |
|
J(n) = ∫0 |
sinn tdt, |
для n 1. √
|
π |
|
Ответ: J(n) ≈ |
|
. |
2n |
||
3. Получить первый член асимптотического разложения интеграла
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
J(α, x) = ∫0 |
exp(−tα/α − xt)dt, |
|
|||||||
если α (0, 1) |
и x 1. |
|
|
|
1 − α |
|
|
||||
|
J(α, x) |
|
|
2π |
|
x−α/[2(1−α)]−1 exp |
|
x−α/(1−α) |
|
||
Ответ: |
≈ √1 − α |
( |
|
). |
|||||||
|
|
|
α |
||||||||
4. Получить первый член асимптотического разложения интеграла
∫1
J(n) = (1 − t2)ndt,
−1
для n 1. √
|
π |
|
Ответ: J(n) ≈ |
|
. |
n |
||
5. Получить первый член асимптотического разложения интеграла
|
|
|
|
∞ |
√ |
eiωtdt |
|
|
|
|
|
|
−∞ |
|
|
|
|
J(ω, α) = ∫ |
|
(α2 + t2)(1 + t2) |
, |
(1.36) |
||||
если ω (α − 1)−1. |
|
|
|
|
||||
Ответ: J(ω, α) = √ |
|
2π |
|
|
|
|
|
|
|
|
e−ω. |
|
|
|
|
||
|
ω(α2−1) |
|
|
|
|
|||
16
1.7.Приближенное интегрирование быстроосциллирующих функций
1.7.1. Метод стационарной фазы
Рассмотрим интеграл вида: |
|
∫b |
|
J(λ) = f(t) eiλS(t) dt, |
(1.37) |
a
где λ – некоторый вещественный параметр, а f(t) и S(t) непрерывные функции. Функцию S(t) будем называть фазовой функцией. Наша задача будет состоять в оценке этого интеграла при больших вещественных значениях параметра λ. Рассмотрим вначале случай, когда на отрезке [a, b], производная функции S(t) не обращается в нуль. Такая ситуация соответствует случаю, когда функция S(t) монотонно возрастает или убывает. Проинтегрируем (1.37) по частям:
|
) eiλS(t) |
|
b |
1 |
b |
|
d f(t) |
|
||||
|
a |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
J(λ) = |
f(t |
a |
− |
|
∫ |
eiλS(t) |
|
|
|
dt. |
(1.38) |
|
iλS′(t) |
iλ |
dt |
S′(t) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Если проинтегрировать (1.38) по частям еще раз, то следующий член разложения интеграла J(λ) будет пропорционален λ−2. Таким образом, продолжая интегрирование по частям, можно построить асимптотический ряд по степеням λ−1. Главный член такого асимптотического разложения имеет вид:
|
[ |
f(b)eiλS(b) |
|
)eiλS(a) |
] , |
|
J(λ) ≈ (iλ)−1 |
|
− |
f(a |
(1.39) |
||
S′(a) |
S′(b) |
и определяется разностью значений подынтегральной функции на концах отрезка интегрирования. Например, следует оценить интеграл
∫∞ |
|
J(λ) = (1 + t)−αeiλtdt, |
(1.40) |
0 |
|
если λ 1. Так как фазовая функция монотонно возрастает, то используя формулу (1.39) получим J(λ) ≈ iλ−1.
Оценим значение интеграла Френеля
∫∞ |
|
J(λ) = eit2 dt, |
(1.41) |
λ
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
если λ 1. Для этого сделаем замену переменной, t = λ |
√ |
|
|
||||||||||
ξ, тогда имеем: |
|||||||||||||
|
λ |
∞ |
iλ2ξ |
|
iλ2 |
|
|
|
|||||
J(λ) = |
∫1 |
e√ |
|
|
dξ ≈ i |
e |
. |
(1.42) |
|||||
|
|
|
|
||||||||||
2 |
2λ |
||||||||||||
ξ |
|||||||||||||
Очевидно, рассмотренный метод эквивалентен методу Лапласа для µ = ν = 1, в том случае, если удается развернуть контур интегрирования вдоль мнимой оси комплексной плоскости.
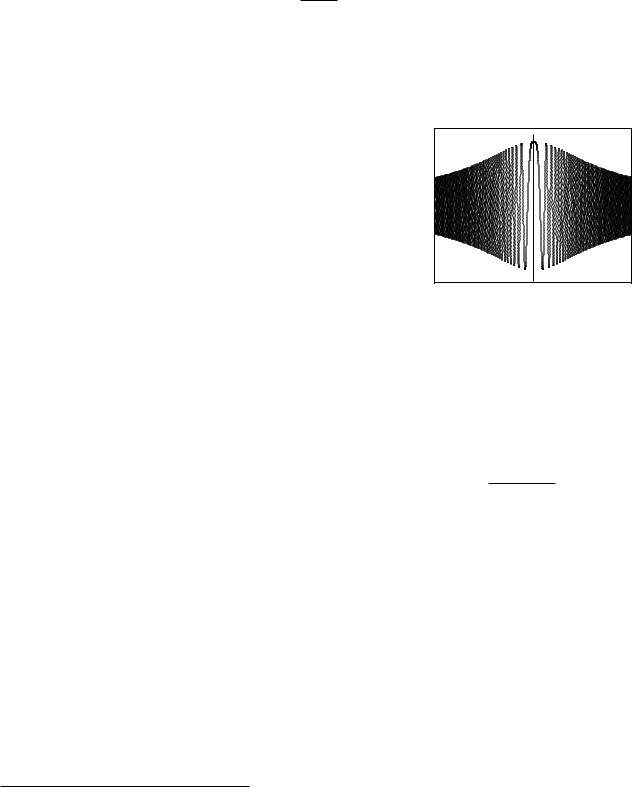
Рассмотрим случай, когда внутри отрезка интегрирования фазовая функ-
ция принимает максимальное (мини- |
) |
|||||||||
iλS(t) |
||||||||||
мальное) значение, т.е. существует точ- |
||||||||||
ка t = t0, где t0 [a, b], для которой |
(e |
|||||||||
S′(t |
|
) |
= 0, и S′′(t |
|
) |
= 0. В окрестно- |
Re |
|||
|
0 |
|
|
0 |
|
̸ |
iS(t) |
меняется |
||
сти точки t0, функция e |
|
|
||||||||
достаточно медленно (см. рис. 1.3), об- |
t0 |
|||||||||
разуя область стационарной фазы, по- |
||||||||||
этому, |
следует ожидать, |
что основной |
|
|||||||
вклад в интеграл будет определяться об-
Рис. 1.3.
ластью стационарной фазы. Тогда, для
оценки интеграла (1.37), разложим функцию S(t) в окрестности точки t0 в ряд Тейлора до второго члена, S(t) ≈ S(t0) + S′′(t0)(t − t0)2/2, функцию f(t) в окрестности точки t0 аппроксимируем ее значением f(t0), а пределы интегрирования увеличим до ±∞:
∞
J(λ) ≈ ∫ |
|
S′′ |
(t0) |
|
2 |
dt = f(t0) eiλS(t0)√ |
πi |
|
|
f(t0) eiλS(t0) eiλ |
|
|
(t−t0) |
|
2 |
. |
(1.43) |
||
|
2 |
|
|||||||
|
|
λS′′(t0) |
|||||||
−∞
Отметим, что наличие стационарной точки внутри отрезка интегрирования модифицирует асимптотическое поведение интеграла. Действительно, если внутри отрезка интегрирования нет точки стационарной фазы, то асимптотика интеграла для λ 1 определяется членом λ−1 (см. формулу (1.39)), однако, если точка стационарной фазы находится внутри отрезка интегрирования, то асимптотика интеграла определяется членом λ−1/2, и интеграл значительно медленнее затухает с ростом λ. Отметим, что если отрезок интегрирования включает несколько точек стационарной фазы, то значение интеграла определяется суммой членов, соответствующих каждой точке стационарной фазы3. Рассмотрим
3Аддитивность вклада стационарных точек, нарушается, если расстояние между точками меньше λ−1=2 и в этом случае оценка интеграла требует специального рассмотрения.
18
ряд примеров иллюстрирующих применение метода стационарной фазы.
Пример 1. Функция Бесселя для z n
Функция Бесселя имеет следующее интегральное представление:
|
|
2π |
|
|
Jn(z) = |
1 |
∫0 |
ei(nt−z sin t)dt. |
(1.44) |
2π |
В нашем случае f(t) ≡ 1, λ = z, S(t) = nz t − sin t. Точки стационарной фазы определяются из уравнения:
S′(t) = |
n |
− cos(t) = 0. |
(1.45) |
z |
Откуда получаем две точки стационарной фазы t1 = arccos(n/z) ≈
π/2 − n/z, t2 = 2π − arccos(n/z) ≈ 3π/2 + n/z, где мы учли, что z n. Значения функции S(t) и ее второй производной дается соответственно выражениями:
|
|
|
−1 + |
|
πn |
|
|
|
|
|
|
|
|
|
3πn |
|
|
|
|
(1.46) |
|||||||||
|
|
S(t1) = |
|
|
, |
S(t1) = 1 + |
|
|
|
|
|
|
|
||||||||||||||||
|
2 z |
|
2 z |
|
|
|
|
||||||||||||||||||||||
|
|
S′′(t1) = 1, |
S′′(t2) = −1. |
|
|
|
|
|
|
|
(1.47) |
||||||||||||||||||
Тогда для функции Бесселя имеем оценку: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
2πi |
|
|
|
|
|
|
|
|
|
|
|
2πi |
|
|
|
|
|
|||||||
Jn(z) ≈ |
|
(e−i(z−nπ/2)√ |
|
|
|
+ ei(z−nπ/2) |
√ |
− |
) = |
|
|
|
|
|
|||||||||||||||
2π |
z |
|
|
z |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
π |
|
nπ |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
cos |
(z − |
|
− |
|
) . |
(1.48) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
πz |
4 |
2 |
||||||||||||||
Пример 2. Функция Эйри для z −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Функция Эйри имеет следующее интегральное представление: |
|
||||||||||||||||||||||||||||
|
|
|
1 |
|
∞ |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Ai(z) = |
∫ |
|
exp |
[i ( |
ξ |
+ zξ)] dξ. |
|
|
|
|
(1.49) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
2π |
|
3 |
|
|
|
|
||||||||||||||||||||
−∞
Используем замену переменной ξ = интеграл (1.49) к виду (1.37). После
|
√ |
∫ |
|||
|
|
|
|
∞ |
|
Ai(z) = |
|
|z| |
|
exp |
|
2π |
|||||
|
|
||||
√
|z|t для того чтобы преобразовать
замены переменной получим: |
|
||
[i|z|3/2 |
(t3 − t)] dξ. |
(1.50) |
|
|
3 |
|
|
−∞

19
Сравнивая (1.50) c (1.37) получим λ = |z|3/2 |
3 |
, S(t) = t3 − t. Точки стацио- |
нарной фазы определяются из элементарного уравнения S′(t) = t2 −1 = 0, и равны, соответственно, t1,2 = ±1. Вычисляя вторую производную от S(t) и используя (1.43) получим:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
exp |
(− |
2 i z 3/2 |
)√ |
i |
+ |
exp |
( |
2 i z |
|
3/2 |
|
√− |
|
i |
|
|
|
|
||||||||
Ai(z) = |
2 |
| | |
π |z| |
|
|
2| | |
) |
|
π |z| |
||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
√ |
|
|
|
π |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3/2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
√ |
|
| |
| |
|
( |
3 |z| |
|
|
− 4 ) . (1.51) |
|||||||
|
|
|
|
|
|
|
|
|
= |
|
π |
√ |
z |
|
cos |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.8. Метод перевала
Рассмотрим асимптотику интеграла вида: |
|
J(λ) = ∫C f(z) eλS(z)dz, |
(1.52) |
где C контур в комплексной плоскости вдоль которого выполняется интегрирование, f(z) и S(z) — аналитические функции комплексного аргумента, λ — большой вещественный параметр. Дополнительно будем предполагать, что кривую интегрирования можно деформировать таким образом, чтобы новый путь интегрирования проходил через точку z = z0, для которой S′(z0) = 04.
Очевидно, точка z = z0 является седловой точкой. Действительно, разложим функцию S(z) в окрестности точки z = z0 в ряд Тэйлора до квадратичных членов:
S(z) ≈ S(z0) + S′′(z0)(z − z0)2/2 = S(z0) + |S′′(z0)|ρ2ei(θ+2φ)/2, (1.53)
где ρ = |z − z0|, θ = arg(S′′(z0)), и φ = arg(z − z0). Поэтому, если путь интегрирования деформирован таким образом, что θ + 2φ = π, то в окрестности z0 Re(S(z) − S(z0)) < 0. В то же время, если θ + 2φ = 0, то Re(S(z) −S(z0)) > 0, т. е. z0 — седловая точка (точка перевала). Таким образом, точка z0 в комплексной плоскости является точкой пересечения линий, определяющих границы областей знакопостоянства разности Re(S(z)−S(z0)). В этом случае удобно деформировать путь интегрирования таким образом, чтобы он прошел через точку перевала z0 в области, где Re(S(z) − S(z0)) < 0. Если дополнительно, вдоль деформированного
4Дальнейшие выводы будут получены в предположении, что точка z0 это простая точка, т. е. S′′(z0) ≠ 0.
20
пути интегрирования выполняется условие θ+2φ = π, то Im(S(z)) = const и подынтегральная функция имеет резкий максимум в окрестности точки z0, который и дает основной вклад в интеграл. Подставляя разложение (1.53) в (1.52) и делая замену переменной z − z0 = ρeiφ, где φ = (π − θ)/2,
получим: |
|
|
|
|
|
|
J(λ) ≈ eλS(z0)eiφ ∫C′ |
f(z)e−λ|S′′ (z0)|ρ2/2dρ. |
(1.54) |
||||
Наконец, используя метод Лапласа для оценки (1.54), имеем: |
|
|||||
|
|
|
|
|
|
|
J(λ) ≈ eλS(z0)eiφ√ |
2π |
(1.55) |
||||
|
. |
|||||
λ|S′′(z0)| |
||||||
Сделаем некоторое замечание относительно полученного соотношения (1.55). А именно, выбор оптимального пути интегрирования в большинстве задач невозможен ввиду сложной функциональной зависимости S(z), тем не менее всегда можно деформировать путь интегрирования таким образом, чтобы он прошел через точку перевала, вклад от которой дается выражением (1.55).
Проиллюстрируем метод перевала на ряде примеров.
1.8.1.Асимптотика функции Эйри для z 1
Для функции Эйри используем интегральное соотношение (1.49), ко- |
|||||||||
торое после замены переменной ξ = √ |
|
|
|
||||||
zt примет вид: |
|
||||||||
√ |
|
∞ |
|
|
|
|
t3 |
|
|
z |
|
|
|
3=2 |
|
||||
Ai(z) = |
|
∫ |
eiz |
( |
3 +t)dξ. |
(1.56) |
|||
2π |
|||||||||
−∞
В данном случае путь интегрирования есть вся действительная ось. Очевидно, контур интегрирования выбран неудачно, так как он не проходит через точку перевала. Точка перевала определяется уравнением:
S′(t) = i(t2 + 1) = 0, |
(1.57) |
из которого получаем два значения для z0: i и −i. Обе точки являются пе-
ревальными, однако только одна из них дает вклад в интеграл. Действи-
( )
тельно, исследуем более детально фазовую функцию S(z) = i |
z3 |
+ z . |
|
3 |
|
Подставляя z в виде z = x + iy и выделяя мнимую и действительную части получим:
2 |
|
|
x2 |
||
ReS(z) = −y (x2 − |
y |
+ 1) , |
ImS(z) = x ( |
|
− y2 + 1) . (1.58) |
3 |
3 |
||||
