3.4 Методы решения матричных игр

Рассмотрим методы решения матричных игр, основанные на использовании свойств оптимальных стратегий.

1. Сведение игры к системе неравенств

Свойство 2 оптимальных стратегий означает, что любая матричная игра может быть сведена к системе уравнений и неравенств.

Пусть – смешанная стратегия первого игрока,– смешанная стратегия второго игрока. Тогда, согласно свойствам 2 оптимальных стратегий, выполняются следующие уравнения и неравенства:

, ,

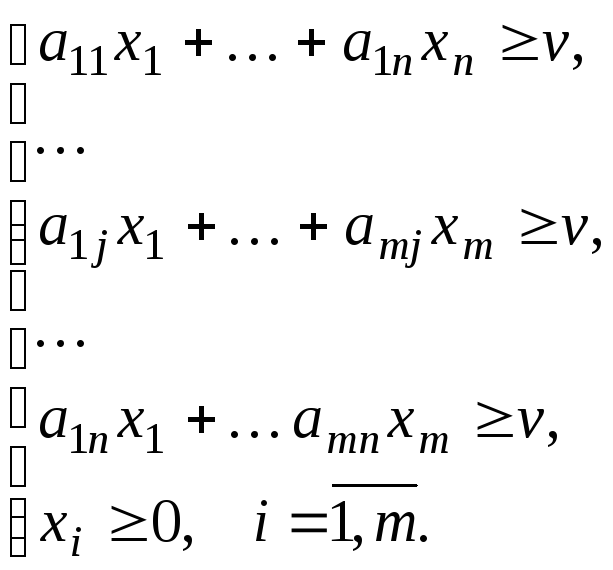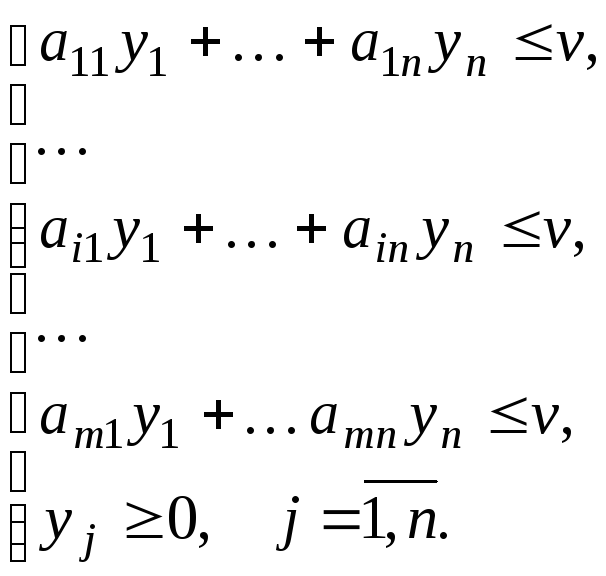(2) (2д)

Решением системы двух уравнений и m+n неравенств, содержащих m+n+1 переменную, являются оптимальные стратегии игроков ,и цена игры.

В случае, если размерность задач оказывается достаточно небольшой, возможно найти решение системы, заменив неравенства уравнениями.

Рассмотрим следующий пример.

Примеры

Пример 1. Найти цену и оптимальные стратегии игроков в игре с матрицей .

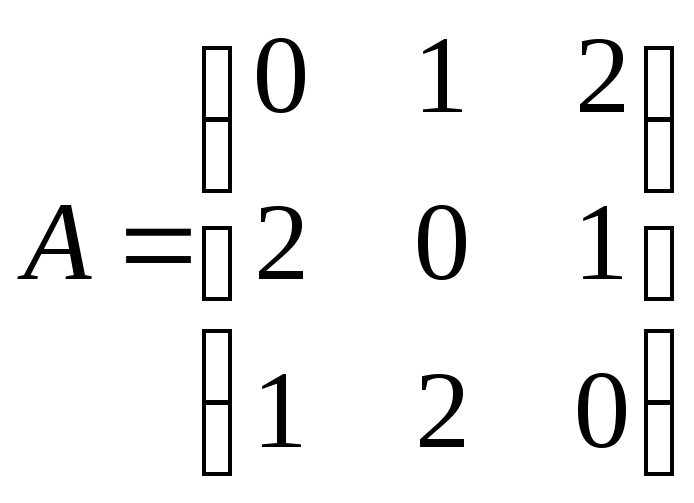Решение

Пусть – смешанная стратегия первого игрока,– смешанная стратегия второго игрока. Выпишем для игры соотношения (2) и (2д):

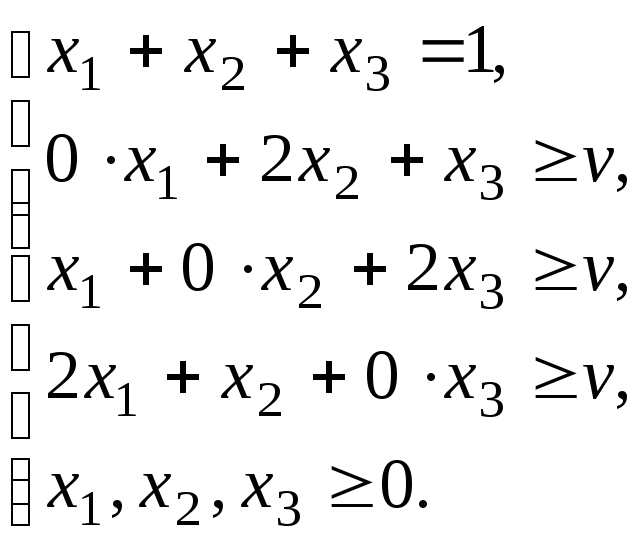
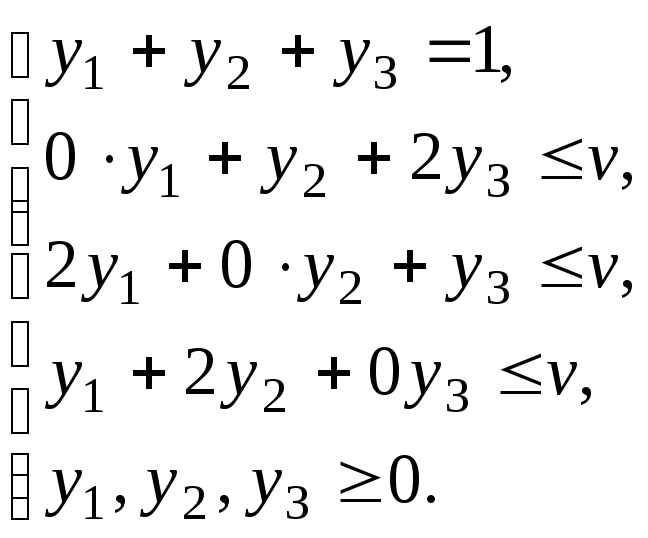
Заменяя системы уравнений и неравенств равенствами и решая полученную систему линейных уравнений, получаем значения искомых величин: , то есть оптимальная стратегия Р1 –, а оптимальная стратегия Р2 –, оптимальное значение цены игры:.

2. Графический (графоаналитический) метод решения игры

Если число стратегий хотя бы одного из игроков равна 2, то оптимальную стратегию этого игрока и оптимальное значение цены игры возможно найти графическим методом, используя свойство 3 оптимальных стратегий:

.

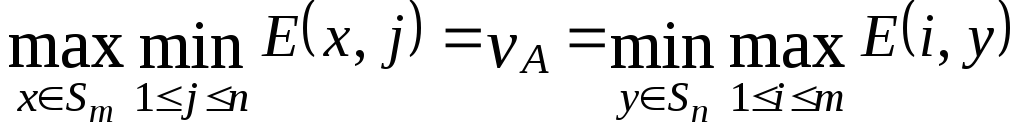1. Рассмотрим игру, в которой игрок 1 имеет две стратегии, а игрок 2 имеет n стратегий. Матрица игры в этом случае представима в виде:

.

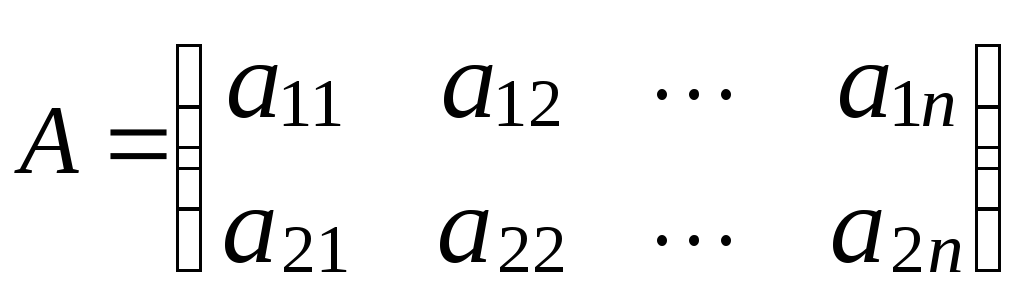Пусть игрок 1 выбрал смешанную стратегию , а игрок 2 чистую стратегиюj. Тогда математическое ожидание выигрыша первого игрока равно:

. (3)

Геометрически оно представляет собой прямую в координатах . Таким образом, каждой чистой стратегииj соответствует своя прямая. Графиком функции

является нижняя огибающая семейства прямых (3). Точка , в которой достигается максимум функциидля, и дает требуемое оптимальное решение, а значение игры.

Примеры

Пример 2. Рассмотрим игру с матрицей .

Для каждого имеем:

Нижняя огибающая семейства прямыхи сами прямые,изображены на рисунке 1.

Максимум функциинаходится на пересечении третьей и второй прямых. Таким образом,– решение уравнения

.

Откуда получаем оптимальную стратегию игрока 1 и

значение игры .

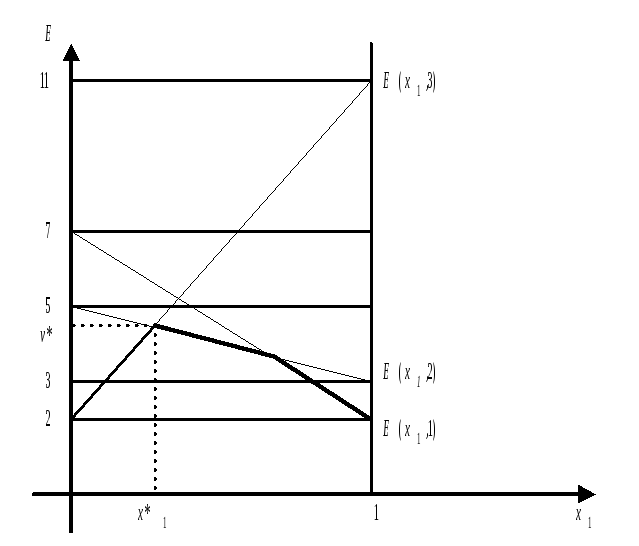
Рис.1

2. Рассмотрим случай, когда 2 стратегии имеет игрок 2, а игрок P1 – m стратегий. Тогда матрица А имеет вид:

.

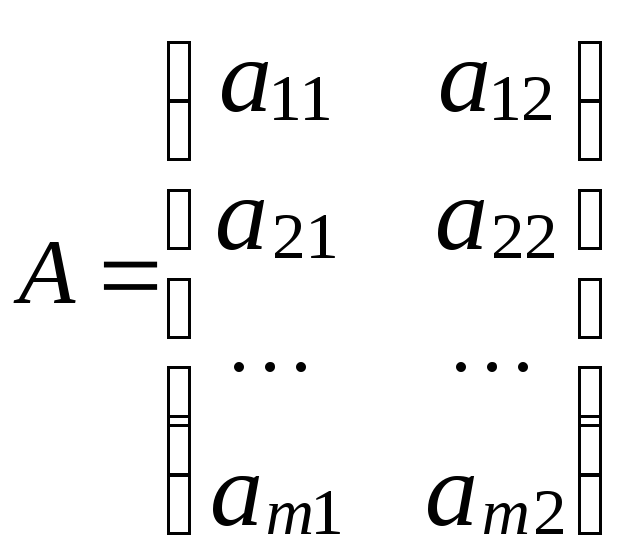Анализ этой игры проводится аналогично. Действительно, пусть – произвольная смешанная стратегия игрока 2. Тогда математическое ожидание проигрыша игрока 2 в ситуацииравно:

.

График функции – прямая. Рассмотрим верхнюю огибающую этих прямых, то есть функцию

.

Точка минимума функциидает оптимальную стратегиюи значение игры.

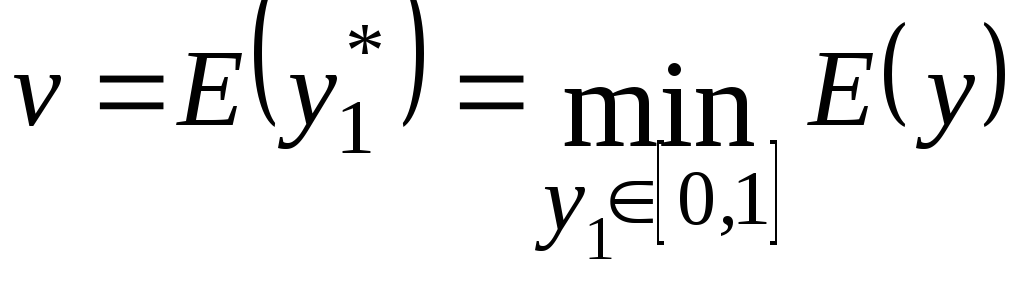Пример 3. Рассмотрим графический метод решения игры с матрицей

.

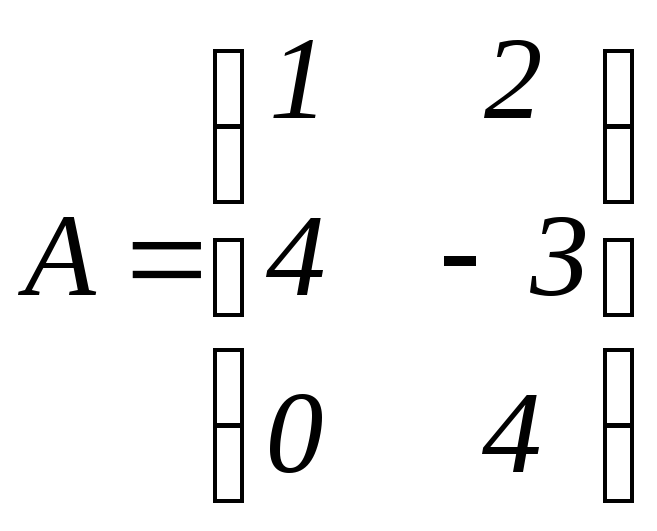Для каждого имеем:

Верхняя огибающая семейства прямыхи сами прямые,изображены на рисунке 2.

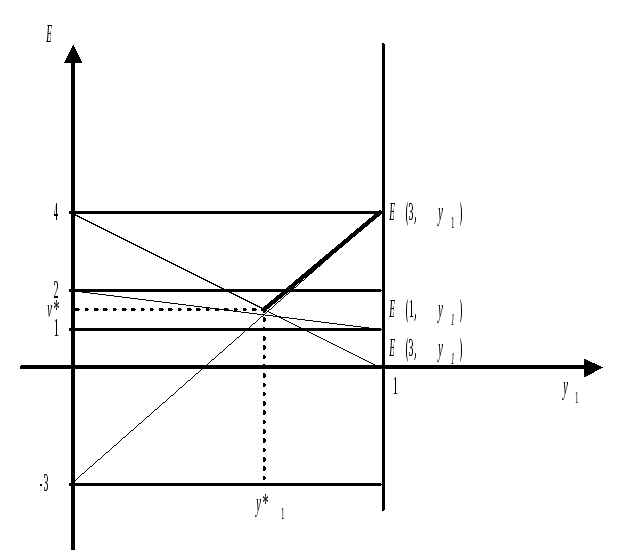
Рис.2

Максимум функциинаходится на пересечении третьей и второй прямых. Таким образом,– решение уравнения.

Откуда получаем оптимальную стратегию игрока 1 и значение игры.