Примеры

Пример 1. Рассмотрим следующую игру. Игроки выбирают одновременно одно из трех чисел: «один», «два», «три». Выигрыш Р1 (проигрыш Р2) положителен и равен названному числу, если он правильно угадал выбор второго игрока и 0 в противном случае.

В данной задаче , а матрица игры имеет следующий вид:

.

Пример 2. Оборона города (игра полковника Блотто).

Полковник Блотто (игрок Р1) имеет 4 полка, а его противник (Р2) – 3 полка. Противник защищает 2 позиции. Позиция будет занята полковником Блотто, если на ней наступающие полки окажутся в численном превосходстве.

При этом, если у полковника Блотто на позиции полков больше, чем у противника, то его выигрыш на этой позиции равен числу полков противника плюс один (за захват позиции). Если у Р2 полков больше, то Р1 теряет все свои полки и 1 за позицию.

Если число полков Р1 и Р2 на позиции одинаково, то имеет место ничья и никто ничего не получает.

Считая, что суммарный выигрыш Р1 равен сумме его выигрышей по двум позициям и игра является антагонистической, сформировать матрицу игры.

Решение

Стратегией первого игрока является пара ,, где– число полков, отправленных Блотто на позицию 1,– на позицию 2. Тогда. Аналогично для второго игрока. Матрица игры имеет следующий вид:

.

Рассмотрим формирование элементов матрицы на примере – величины выигрыша Р1 при условии, что он предпринял стратегию (4,0), а второй игрок стратегию (1,2). На первой позиции полки полковника Блотто оказываются в численном превосходстве (4>1), поэтому он выигрывает число полков противника (1) плюс 1 за захват позиции (всего выигрыш по позиции равен 2). На второй позиции наоборот, полки Р2 оказываются в превосходстве (0<2) и тогда Блотто теряет все свои полки на этой позиции (0) и 1 за поражение на позиции (всего выигрыш по позиции равен -1). Суммарный выигрыш Блотто по двум позициям:. Аналогично формируются остальные элементы матрицы.

3.2 Ситуация равновесия в чистых стратегиях: понятие и существование

Рассмотрим антагонистическую игру . Каждый из игроков выбором стратегии стремится максимизировать свой выигрыш, который для Р1 определяется величиной, а для второго игрока величиной. Выигрыши игроков определены на ситуацияхи поэтому в своем поведении каждый игрок должен учитывать поведение противника.

В теории игр предполагается, что оба игрока ведут себя рационально, то есть стремятся получить максимально возможную величину гарантированного выигрыша. Пусть игрок 1 выбрал стратегию x. Тогда в худшем случае он может получить величину . Р1 может себе гарантировать получение, по крайней мере, величины выигрыша, которая называетсянижней ценой игры или максимином. С другой стороны, игрок 2 может себе гарантировать величину проигрыша не меньшую, чем , называемуюверхней ценой игры или минимаксом.

Замечание 1. Для матричной игры ,.

Лемма 1. Для любой антагонистической игры справедливо:.

Рассмотрим вопрос оптимального поведения игроков. Ситуация называетсяравновесной в игре , если Р1 невыгодно отклоняться от стратегиии второму игроку от стратегиипри условии, что противник придерживается равновесной стратегии.

Определение 3. В антагонистической игре ситуацияназывается ситуацией равновесия или седловой точкой, если выполнены следующие неравенства:

, для всех стратегий ,.

Так как , то при условии, что второй игрок выбрал стратегию, игрокуP1 невыгодно выбирать любую стратегию , так как при этом его выигрыш не увеличится. Аналогично, используя правую часть неравенства (1), приходим к выводу, что отклонение отневыгодноP2.

Замечание 2. В матричной игре ситуация называется ситуацией равновесия или седловой точкой матрицыА, если выполняются неравенства: ,,. Другими словами, элементявляется одновременно минимумом в строкеи максимумом в столбце.

Свойства ситуаций равновесия

Пусть ,– ситуации равновесия в антагонистической игре. Тогда справедливо следующее:

1) ;

2) ,– ситуации равновесия.

Необходимые и достаточные условия существования ситуации равновесия в чистых стратегиях доказываются следующей теоремой.

Теорема 1. Для того, чтобы в игре существовала ситуация равновесия, необходимо и достаточно, чтобы существовали верхняя и нижняя цены игры:

, ,

и выполнялось равенство: .

Доказательство

1. Необходимость.

Пусть – ситуация равновесия. Докажем, что. Согласно лемме 1,, и поэтому достаточно показать выполнение неравенства.

По определению ситуации равновесия:

, ,.

Тогда , а следовательно,.

Так как , то

. (*)

Аналогично:

. (**)

Из (*), (**) следует: , что и требовалось доказать.

2. Достаточность.

Пусть существуют ,и выполнено равенство. Конструктивно докажем существование ситуации равновесия в этом случае.

Пусть и;

и .

Докажем, что – ситуация равновесия.

;

.

Тогда, так как правые части неравенств равны по условию, то

,

и

, ,, что и требовалось доказать.

В случае если верхняя цена игры и нижняя совпадают, величину называютценой игры.

Для антагонистической игры справедлива следующая лемма о масштабе.

Лемма 2. ( Лемма о масштабе)

Пусть и –две антагонистические игры, причем , где,– некоторые константы. Тогда множества оптимальных стратегий игроков висовпадают, а.

Примеры

Пример 1. Найти верхнюю и нижнюю цены игры и ситуацию равновесия, при условии, что она существует, если матрица имеет вид:

.

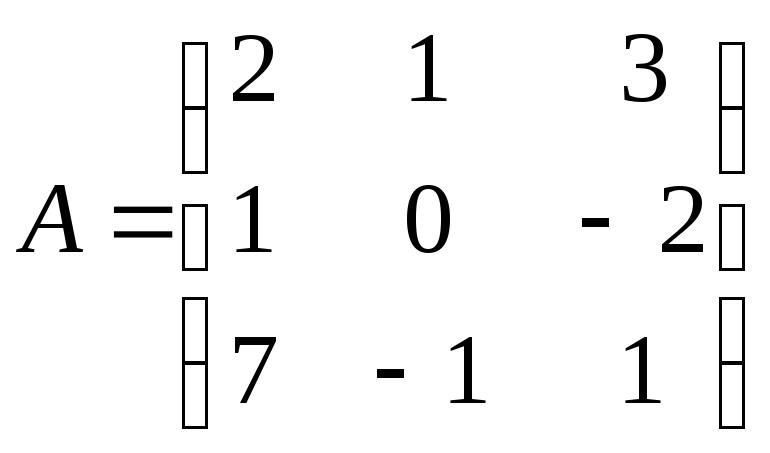Решение

Найдем нижнюю цену игры.

Если Р1 выберет первую стратегию, то он получит гарантированно .

Если Р1 выберет стратегию 2, то он получит гарантированно .

Если Р1 выберет стратегию 3, то он получит гарантированно .

Тогда выбором своей стратегии Р1 может получить, по крайней мере не меньше .

Найдем верхнюю цену игры.

Если Р2 выберет первую стратегию, то он проиграет гарантированно не больше .

Если Р2 выберет стратегию 2, то он проиграет гарантированно не больше .

Если Р2 выберет стратегию 3, то он проиграет гарантированно не больше .

Тогда выбором своей стратегии Р2 может проиграть, по крайней мере, не меньше . Так как=1, то равновесием является параиv=1.

Пример 2. Пусть дана матрица выигрышей игрока P1 . Найти ситуации равновесия.

Решение

В данной игре ,, и поэтому игра не имеет ситуации равновесия. Если игрокP1 выбирает свою чистую максиминную стратегию , то игрокP2, выбрав свою минимаксную стратегию , проигрывает только 20 единиц. В этом случаеP1 выгодно выбрать стратегию , то есть отклониться от своей максиминной стратегии и выиграть 30. ТогдаP2 будет выгодно отклониться от своей чистой минимаксной стратегии и проиграть 10. В свою очередь, игрок P1 должен выбрать свою 2-ю стратегию, чтобы выиграть 40, а P2 ответит выбором 2-й стратегии и т. д.