
ОСНОВЫ МЕХАНИКИ_пособие
.pdf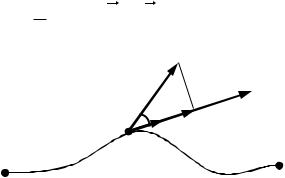
Из (3.1) видно, что работа под действием силы не совершается в двух случаях:
1)точка приложения силы неподвижна ( dr 0 );
2)α π2 , то есть F V .
|
|
F |
|
|
|
М |
α |
|
v |
|
|
FS |
|
|
|
|
|
2 |
|
1 |
|
dr |
|
|
|
|
|
Рис.3.1. К определению понятия «работа силы»
Работа – величина аддитивная, это означает, что работа силы на участке траектории 1-2 равна алгебраической сумме элементар-
ных работ на всех бесконечно малых участках пути. Эта сумма сво- |
|
дится к интегралу |
α |
S2 |
S2 |
A |
Fcosαds FSds . |
S1 |
S1 |
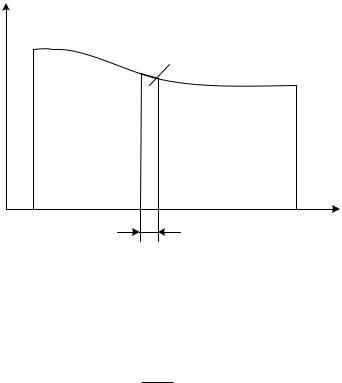
Если зависимость FS |
от пути s вдоль траектории 1-2 пред- |
ставить графически (рис.3.2), работа A определяется на графике как площадь заштрихованной фигуры.
Единица работы – джоуль (Дж): 1 Дж – работа, совершаемая телом под действием силы 1 Н на пути 1 м (1 Дж = 1 Н·м).
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:
N A . dt
33
Fs |
|
|
|
|
dA |
|
|
|
A |
|
|
S1 |
dS |
S2 |
S |
|
Рис.3.2. Работа на участке траектории ( S1 ,S2 ) |
|
|
|
|
За время dt сила F совершает работу |
Fdr , и мощность, |
развиваемая телом под действием этой силы в данный момент времени
Fdr N dt Fv .
Мощность – величина скалярная; единица мощности – ватт (Вт): 1 Вт – мощность, при которой за время 1 с совершается работа
1 Дж (1 Вт =1 Дж/с).
3.2. Консервативные и диссипативные силы
Кроме контактных взаимодействий, возникающих между соприкасающимися телами, наблюдаются взаимодействия между телами, удаленными друг от друга. Такие взаимодействия осуществляют-
ся посредством физических полей.
34

Стационарное поле, в котором работа, совершаемая над частицей силами поля, зависит лишь от начального и конечного положений частицы и не зависит от пути, по которому она двигалась, называют потенциальным. Силы, действующие в потенциальных полях, называют консервативными. Работа консервативной силы на замкнутом пути равна нулю. Примеры консервативных сил – сила тяжести, сила упругости.
Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называет-
ся неконсервативной (или диссипативной). Типичные неконсерватив-
ные силы – силы трения.
3.3. Кинетическая и потенциальная энергия
Кинетическая энергия T механической системы – это энер-
гия механического движения этой системы.
Работа A силы F на пути, который тело прошло за время
возрастания скорости от 0 до V , идет на увеличение кинетической
энергии dT тела, т.е.
A dT .
Но A Fdr m ddtV dr mVdV mVdV dT ,
откуда
V |
|
T mVdV mV2 . |
|
0 |
2 |
|
|
Таким образом, тело массы m , движущееся со скоростью V , обладает кинетической энергией
mV2
T 2 .
35
Кинетическая энергия – величина аддитивная. Так, энергия системы из n материальных точек равна сумме кинетических энергий этих материальных точек
n |
2 |
|
|
T |
miVi |
. |
|
2 |
|||
i 1 |
|
Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при элементарном изменении конфигурации системы равна приращению потенциальной энергии, взятому с обратным знаком, так как работа совершается за
счет убыли потенциальной энергии системы:
A dП .
Но A Fdr , тогда Fdr dП и потенциальную энергию системы можно найти как
П Fdr C ,
где
Fx
где
C - постоянная интегрирования, то есть потенциальная энергия
может быть определена с точностью до некоторой произвольной постоянной. Поэтому потенциальную энергию тела в ка- ком-то положении полагают равной нулю, а энергию в других положениях отсчитывают относительно этого нулевого уровня (за нулевой уровень можно принять, например, уровень пола, уровень моря и т.д.).
Для консервативных сил
|
П |
, |
Fy |
П , |
Fz |
|
П |
или F gradП ,(3.2) |
||||
|
x |
|
|
y |
|
|
|
z |
|
|
|
|
|
|
|
gradП |
П |
|
П |
П |
|
|
|||
|
|
|
x |
i |
y |
j |
z |
k. |
(3.3) |
|||
|
|
|
|
|
|
|
|
|
|
|||
36

Вектор, определяемый выражением (3.3), называется градиен-
том скаляра П.
Таким образом, выражение (3.2) показывает, что консервативная сила равна градиенту потенциальной энергии, взятому с обратным знаком.
Потенциальная энергия тела массой m , поднятого на высо-
ту h над поверхностью Земли, равна
П mgh ,
где высота h отсчитывается от уровня, для которого П0 0.
Потенциальная энергия упругодеформированного тела (пру-
жины)
П
kx2
2
Полная механическая энергия E
ской и потенциальной энергий системы:
.
системы – сумма кинетиче-
ET П .
3.4.Закон сохранения энергии
Рассмотрим систему из n материальных точек массами mi ,
движущихся со скоростями Vi ( Vi << c ). Пусть F i и Fi - равнодействующие внутренних и внешних консервативных сил, действую-
щих на i -ю точку, а f i - равнодействующая внешних неконсерва-
тивных сил, действующих на i -ю точку. Уравнения второго закона Ньютона для этих точек:
37

m1 dV1 F 1 F1 f 1 dt
m2 dV2 F 2 F2 f 2 dt
............................................
mn dVn F n Fn f n . dt
За интервал dt точки совершают перемещения dri . Умножим каждое уравнение на соответствующее перемещение и учиты-
вая, что dri Vidt , получим
|
|
F1 |
dr1 |
f 1dr1 |
|
m1 V1dV1 F 1 |
|||
|
|
F2 |
dr2 |
f 2dr2 |
|
m2 V2dV2 F 2 |
|||
|
.................................................................. |
|||
|
|
Fn |
drn |
f ndrn . |
|
mn VndVn F n |
|||
Сложив эти уравнения, получим |
|
|
||
n |
n |
|
|
n |
|
|
|
|
|
mi VidVi F i Fi dri f idri . |
||||
i 1 |
i 1 |
|
|
i 1 |
n |
n |
|
|
|
Здесь mi Vi dVi d mi Vi2 /2 dT – прираще- |
||||
i 1 |
i 1 |
|
|
|
ние кинетической энергии системы; n
F i Fi dri dП
i 1
- работа внутренних и внешних консервативных сил, взятая с обрат-
38

ным знаком, равная приращению потенциальной энергии системы; n
f i dri - работа внешних неконсервативных сил, действующих i 1
на систему. Итак, имеем
d T П A .
Изменение полной механической энергии при переходе системы из состояния 1 в состояние 2 равно работе внешних неконсервативных сил:
2 |
|
d T П A12 . |
|
1 |
|
Если внешние неконсервативные силы |
отсутствуют, то |
A 0 d T П 0 , откуда |
|
Т П Е const , |
(3.4) |
т.е. полная механическая энергия системы сохраняется. Выражение
(3.4) представляет собой закон сохранения механической энергии: в
системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т.е. не изменяется со временем.
Механические системы, где действуют только консервативные силы (внутренние и внешние), называются консервативными системами. В консервативных системах полная механическая энергия остается постоянной, могут происходить лишь превращения кинетической энергии в потенциальную и наоборот. В частности, этот закон справедлив и для замкнутых консервативных систем.
В диссипативных системах механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) виды энергии. Этот процесс называется диссипацией (или рассеянием) энергии. Строго говоря, все системы в природе являются диссипативными.
39
В системе, где действуют также неконсервативные силы, полная механическая энергия не сохраняется, и закон сохранения механической энергии несправедлив. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой.
Отметим, что закон сохранения энергии – фундаментальный закон природы, он справедлив как для систем макроскопических тел, так и для систем микротел.
3.5.Применение законов сохранения энергии и импульса
ксоударению абсолютно упругих и неупругих тел
Соударение (удар) – это столкновение двух или более тел, при котором взаимодействие длится очень короткое время. Ударные силы столь велики, что внешними силами можно пренебречь; это позволяет систему тел в процессе соударения рассматривать как замкнутую и применять к ней законы сохранения.
Удар называется центральным, если тела до удара движутся вдоль прямой, соединяющей их центры.
Абсолютно упругий удар – столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций (механическая энергия не переходит в другие, немеханические виды) и вся кинетическая энергия, которой тела обладали до удара, после удара снова превращается в кинетическую энергию. В этом случае выполняются закон сохранения импульса и закон сохранения кинетической энергии.
Рассмотрим центральный абсолютно упругий удар двух шаров. Обозначим скорости шаров массами m1 и m2 до удара v1 и
v2 , после удара – v1' и v'2 (рис.3.3). Законы сохранения импульса
и энергии при этом имеют вид:
m1v1 m2v2 m1v'1 m2v'2
40

|
|
|
m v |
2 |
|
|
|
|
|
m |
v |
2 |
|
|
|
|
'2 |
|
m |
'2 |
|
||||||
|
|
|
|
|
|
|
|
2 |
|
|
m v 1 |
|
v 2 |
|
|||||||||||||
|
|
|
1 |
1 |
|
|
2 |
|
|
|
1 |
|
|
2 |
|
|
|
. |
|||||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Решая эти уравнения, находим |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
v' |
|
m1 m2 v1 2m2v2 |
|
|||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
m1 |
m2 |
|
|
|
|
, |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
v' |
|
|
|
|
m2 m1 |
v2 2m1v1 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
m1 m2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
m |
1 |
|
|
|
|
|
m2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
до |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
удара |
|
|
|
|
|
|
|
|
|
|
|
v1 |
|
|
|
v2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
m |
1 |
|
|
|
|
|
|
m2 |
|
|
|
|
|
||
|
|
после |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
удара |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v'1 |
|
|
|
|
|
v' |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
Рис.3.3. Абсолютно упругий удар двух тел |
|
|||||||||||||||||||||||
Частные случаи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1) если |
m m |
2 |
|
, то |
|
v' v |
2 |
и |
v' |
v |
(шары обмени- |
||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
1 |
|
||||||
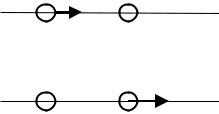
ваются скоростями). Например, при столкновении первого шара с
неподвижным |
вторым |
( v2 0 ) |
первый шар останавливается |
|||
( v' |
0 ), а |
второй |
движется со |
скоростью первого ( v' |
v |
) |
1 |
|
|
|
2 |
1 |
|
(рис.3.4).
41
2) |
если |
|
m2 >> m1 |
(столкновение шара со стен- |
||||
кой), v' |
2v |
2 |
v |
, |
v' |
v |
2 |
(скорость стенки не изменится). |
1 |
|
1 |
|
2 |
|
|
||
При столкновении шара с неподвижной стенкой ( v2 0 ) получим
v1' v1 , то есть шар отскакивает с первоначальной скоростью, меняя направление на противоположное.
до |
m1 |
m2 |
|
|
|
удара |
v1 |
|
|
|
|
после |
m1 |
m2 |
|
|
удара |
v 1 |
|
Рис.3.4. Абсолютно упругий удар тел с равными массами
Абсолютно неупругий удар – столкновение двух тел, в ре-
зультате которого тела движутся вместе либо покоятся. Кинетическая энергия тел полностью или частично переходит в их внутреннюю энергию. В этом случае выполняется закон сохранения импульса. Закон сохранения механической энергии не выполняется, выполняется закон сохранения суммарной энергии – механической и внутренней.
Рассмотрим центральный абсолютно неупругий удар двух шаров массами m1 и m2 , имеющих до удара скорости v1 и v2 .
После удара они будут двигаться с общей скоростью v (рис.3.5), которую найдем из закона сохранения импульса:
m1v1 m2v2 m1 m2 v , |
v |
m1v1 m2v2 |
. |
|
|||
|
|
m1 m2 |
|
42 |
|
|
|
