Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Башкирский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3курс, VIсем.Волков,Ягола инт ур

.pdf

Скачиваний:

Добавлен:

18.03.2016

Размер:

1.23 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 108 9 10 > Следующая >>>

Если бы h1 (x),

h2 (x) были бы независимыми, то мы получили бы систему уравнений

Эйлера. Однако

h1 (x), h2 (x)

подчиняются (по крайней мере, для малых t) уравнению

связи

Φ[x, y + th1 , z + th2 , y′+ th1′, z′+ th2′]= 0 .

h2 (x) через h1 (x) .

Получим

уравнение,

решая

которое,

мы

сможем выразить

Продифференцируем записанное выше равенство по

и положим

t = 0 . Тогда

dΦ

= 0

или

t =0

Φy h1 +Φy′h1′ +Φz h2 +Φz′h2′ = 0 .

Так как Φz′ ≠ 0 ,

то

Φy

Φy′

h2′ = −

h1′.

h2 −

h1 −

z′

Обозначив

= −

z , a

= −

Φy

b = −

Φy′

получим следующую задачу Коши для

Φz′

отыскания

h2 (x)

при условии, что

h1 (x) задано:

+b h′);

h′

= a

h +(a h

h2 (a) = 0.

Уравнение,

которому удовлетворяет h2 (x) ,

является линейным дифференциальным

уравнением первого порядка. Общее решение этого уравнения хорошо известно из курса дифференциальных уравнений и может быть найдено, например, методом вариации постоянной. Получите самостоятельно это общее решение и покажите, что решение задачи Коши имеет вид

x	+b1h1′)exp	x
h2 = ∫(a1h1	+b1h1′)exp		∫a2dη	dξ.
a			ξ

Итак, мы выразили h2 (x) через h1 (x) . Подставляя это выражение во второй

интеграл в формуле для вариации, после простых преобразований (изменение порядка интегрирования по x и ξ ) получаем

∫ Fz −

Fz′ dx∫(a1h1

+b1h1′)exp

∫a2dη

dξ = ∫(a1h1

+b1h1′)dξ∫ Fz −

Fz′ exp

∫a2dη

′

∫(

a h

+b h

γ (ξ)dξ =

∫

a γ −

(

b γ

)

h dξ,

1 1

1 1 )

где

γ (ξ) = ∫

Fz −

Fz′ exp

∫a2dη

dx .

Переобозначив переменную интегрирования ( x вместо ξ ), окончательно получим

δV = ∫

−

Fy′ + a1 γ −

(b1γ )

h1 (x) dx = 0 .

Здесь

γ (x)

∫

−

exp

∫

dη

dξ .

dξ

z '

Φz '

По основной лемме вариационного исчисления:

−

′ + a

γ −

γ) = 0 .

Вспомнив, что

a = −

Φy

, b = −

Φy′

, получим

Φz′

a1γ −

(b1γ ) = −

Φy

Φy′

−

Φz′

Обозначим λ(x) = −

γ (x) . Очевидно, что λ(x) - дифференцируемая функция.

Тогда

Φz'

a γ −

(b γ ) = λΦ

−

(λΦ

′) ,

и равенство нулю вариации приводит к уравнению

−

′ +λΦ

−

(λΦ

′) = 0 ,

или

+λΦ

−

′ +λΦ

′ ) = 0 .

Мы получили первое из уравнений Эйлера, фигурирующих в условиях теоремы. Перепишем второе уравнение таким образом:

(λΦ

) =

Φz

(λΦ

) +

−

z′

Φz′

Рассмотрим это уравнение как уравнение относительно

λΦz' .

Тогда

λΦ

′ =

∫

−

F ′

exp

∫

dη

dξ

Φz′

является его решением. Сравнивая полученное выражение с выведенной ранее формулой γ (x) = −λΦz′ , получаем, что второе уравнение из системы уравнений Эйлера тоже

выполнено. Теорема доказана.

Рассмотрим теперь задачу с голономной связью. Требуется найти экстремум функционала

			′ ′
		V[ y, z] = ∫F (x, y, z, y , z )dx
		a
при выполнении граничных условий
		y(a) = y0 , y(b) = y1;
		z(a) = z0 ,	z(b) = z1
и уравнения связи	Φ(x, y, z) = 0 .
Граничные	условия	нельзя считать	независимыми,	поскольку Φ(a, y0 , z0 ) = 0 и
Φ(b, y1 , z1 ) = 0 .
Как и ранее, введем функцию H = F +λ(x)Φ и функционал
		b	′ ′
			′ ′
		∫H (x, y, z, y , z ) dx .
		a
В отличие	от задачи с неголономной связью,			теперь Φz′ ≡ 0.	Поэтому
предположим, что Φz ≠ 0 .		Система уравнений Эйлера в данном случае имеет вид:

(Fy

(Fz

+λΦy ) − dxd Fy′ = 0;

+λΦz ) − dxd Fz′ = 0.

Теорема (Необходимое условие экстремума для задачи с закрепленными концами и голономной связью).

Пусть:

1)функции y(x) и z(x) реализуют экстремум в поставленной выше задаче с голономной связью и дважды непрерывно дифференцируемы;

2)функция F непрерывна со своими частными производными до второго порядка включительно;

3)функция Φ непрерывна со своими частными производными, причем Φz ≠ 0 .

Тогда существует непрерывная функция λ(x) такая, что y(x) и z(x) удовлетворяют

системе уравнений, записанной выше.

Доказательство. Выражение для вариации функционала получено при доказательстве предыдущей теоремы и имеет следующий вид:

δV = ∫b [(Fy −	d	Fy′)h1	+(Fz −	d	Fz′)h2 ]dx = 0 .
	dx			dx
a
Выражая теперь h2 через h1 из соотношения			Φy h1 + Φz h2 = 0, полученного также, как

и в предыдущей теореме, и используя условие Φz ≠ 0 , находим

h2 = − Φy h1 .

Φz

Далее, подставляя h2 в выражение для вариации и применяя основную лемму вариационного исчисления, получаем уравнение

−

′) −(F

−

′)

Φy

= 0 .

Φz

−

′

Полагая λ = −

, получаем

первое

уравнение из системы уравнений Эйлера.

Φz

Второе уравнение системы – это записанное выше определение λ . Очевидно, что λ = λ(x) - непрерывная функция. Теорема доказана.

В качестве простого примера рассмотрим задачу об отыскании так называемых геодезических линий. Пусть уравнение Φ(x, y, z) = 0 задаёт некоторую поверхность в

трёхмерном пространстве, на которой фиксированы две точки. Поставим задачу отыскания геодезической линии, т.е. кривой минимальной длины, соединяющей эти точки.

Если предположить, что уравнение кривой допускает введение параметризации с помощью параметра x , то данная задача сводится к минимизации функционала

b
V[ y, z] = ∫	′ 2	′	2	dx
V[ y, z] = ∫	1+( y )	+(z )		dx

ссоответствующими граничными условиями.

Взаключение параграфа рассмотрим так называемую изопериметрическую задачу. Пусть требуется найти экстремум функционала

V[ y] = ∫b F (x, y, y′)dx

при выполнении граничных условий

y(a) = A,	y(b) = B
и дополнительного условия связи
b	′	= l
	′
I[ y] = ∫G(x, y, y ) dx
a
(функционал I[ y] имеет заданное значение).
Задача называется изопериметрической, т.к. если положить
b
I[ y] = ∫	′ 2	dx	= l ,
I[ y] = ∫	1+( y )	dx	= l ,
a			экстремум функционала V [ y] ,
то требуется найти кривую, на которой	достигается		экстремум функционала V [ y] ,

проходящую через заданные точки, причем длина кривой (ее периметр) задана.

Для того, чтобы применить полученные в данном параграфе результаты, введем новую функцию

′

z(x) = ∫G(x, y, y ) dx .

Очевидно, что z(a) = 0, z(b) = l .

Перепишем изопериметрическую задачу в следующем

виде: найти экстремум функционала

V[ y, z] = ∫F

′

(x, y, y )

при выполнении граничных условий

y(a) = A,

y(b) = B , z(a) = 0, z(b) = l и уравнения

неголономной связи

′

Φ(x, y, z, y

, z ) ≡ −z

+G(x, y, y ) = 0 .

Запишем систему уравнений Эйлера для функционала

∫b H dx , где H = F +λΦ :

+λG

) −

(F ′ +λG

′ ) = 0;

dλ

= 0.

Обратите внимание на второе уравнение, из которого следует, что λ = const .

Теорема (Необходимое условие экстремума для изопериметрической задачи с закрепленными концами).

Пусть:

	b
1) функция y(x) реализует экстремум функционала	′	и
1) функция y(x) реализует экстремум функционала	V[ y] = ∫F (x, y, y )dx	и
дважды непрерывно дифференцируема;	a
дважды непрерывно дифференцируема;

2)функции F и G непрерывны вместе со своими частными производными до второго порядка включительно.

Тогда существует число λ такое, что y(x) удовлетворяет уравнению Эйлера

для функционала ∫b H dx , где H = F +λG .

Доказательство следует немедленно из теоремы о необходимом условии для задачи с закрепленными концами и неголономной связью.

Рассмотрим теперь задачу отыскания кривой заданной длины, ограничивающей

максимальную площадь.

В этом

случае,

F = y , V[ y] = ∫y dx ,

G =

′

1+( y )

′

, λ = const .

H = y +λ 1+( y )

Первый интеграл для уравнения Эйлера имеет вид

′

или

H − y H y′ = C1

′ 2

′

y′

= C1 .

y +λ 1+( y )

− y λ

′

1+( y )

Приводя подобные члены, получим

y −C1 = −λ

′ 2

1+( y )

Введём вспомогательный параметр t

по формуле y′ = tg t . Тогда y −C1 = −λcos t .

Найдем x(t) . Имеем

dx = dy

= λsin t dt = λ cos tdt

x −C2 = λsin t .

y′

tgt

Исключая параметр t , получим уравнение окружности

(x −C

+( y −C )2 = λ2 .

Параметры C1 , C2 и λ можно определить из системы:

(x −C

+( y −C )2 = λ2 ;

y(b) = B;

y(a) = A,

∫Gdx = l .

Экзаменационные вопросы

1)Определения и формулировки теорем.

1.	Сформулировать	постановку			задачи	поиска	экстремума	функционала
	b	′	′	)dx при условии, что концы закреплены, и имеется неголономная
		′	′
	V [y, z]= ∫F (x, y, z, y , z
	a
	связь. Записать необходимые условия экстремума в этой задаче.
2.	Сформулировать	постановку			задачи	поиска	экстремума	функционала
	b	′	′	)dx при условии, что концы закреплены, и имеется голономная
		′	′
	V [y, z]= ∫F (x, y, z, y , z

связь. Записать необходимые условия экстремума в этой задаче.

3.Сформулировать определение геодезической линии.

4.Сформулировать изопериметрическую задачу с закрепленными концами и необходимые условия экстремума в этой задаче.

2)Утверждения и теоремы, которые необходимо уметь доказывать. Теоретические задачи.

	b		)dx ,
1.	′	′
1.	Получить необходимые условия экстремума функционала V [y, z]= ∫F (x, y, z, y , z
	a
	если концы закреплены, и имеется неголономная связь.
	b		)dx ,
2.	′	′
2.	Получить необходимые условия экстремума функционала V [y, z]= ∫F (x, y, z, y , z

если что концы закреплены, и имеется голономная связь.

3.Получить необходимые условия экстремума в изопериметрической задаче с закрепленными концами.

4.Записать постановку и привести решение задачи об отыскании кривой заданной длины, площадь под которой максимальна (задача Дидоны).

x1 = B[y].

1+( y′)2 dx .

Лекция №11

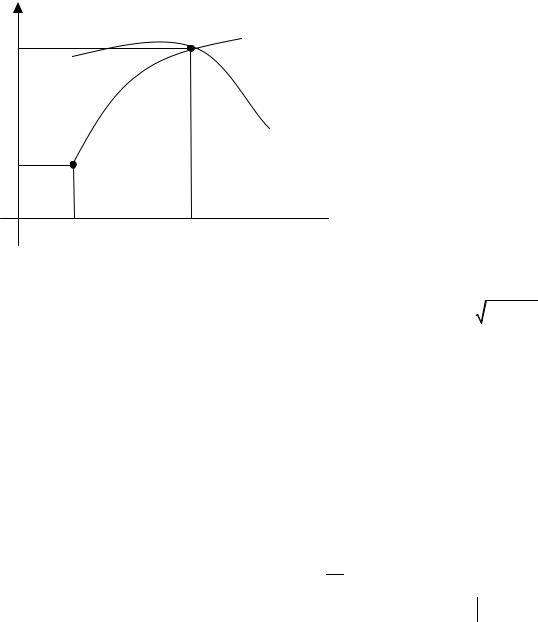
§5. Задачи с подвижной границей.

Рассмотрим задачу минимизации функционала

V [y]= ∫F (x, y, y′) dx

при условии, что левый конец функции, на которой достигается экстремум, закреплен: y(a) = y0 ,

а правый может перемещаться вдоль заданной кривой y =ϕ(x) (см. рисунок, x1 - абсцисса точки пересечения кривых y(x) и ϕ(x) , x [a, b] ).

y(x)	ϕ(x)

a x1 x

Пример: пусть требуется найти расстояние от точки на плоскости с координатами

(a, y0 ) до кривой y =ϕ(x) . Задача сводится к минимизации функционала ∫

Введем функционал B[y], полагая

Теорема (Необходимые условия экстремума для задачи с левым закрепленным и правым подвижным концами).

Пусть

1) y(x) осуществляет экстремум в поставленной выше задаче с подвижной границей и дважды непрерывно дифференцируема;

2)F – функция, непрерывная со своими частными производными до второго порядка включительно;

3)ϕ(x) непрерывна с первой производной. Тогда:

1)y(x) удовлетворяет уравнению Эйлера Fy − dxd Fy′ = 0 ;

2)при x = x1 выполнено условие трансверсальности (F −( y′−ϕ′)Fy′ ) x=x1 = 0 .

Доказательство. Прежде всего, докажем, что выполняется уравнение Эйлера. В самом деле, если y(x) такова, что на ней реализуется экстремум функционала V[ y] в

классе функций, у которых один конец закреплен, а другой подвижен, то на ней реализуется экстремум и в классе функций, когда оба конца закреплены (т.е. задано

граничное условие на правом конце	y(x1 ) =ϕ(x1 ) ,	где x1 –	абсцисса точки	пересечения
функции, на которой достигается	экстремум, с	кривой	y =ϕ(x) ). Как	доказано в

параграфе 3 для задачи с закрепленными концами, в этом случае выполняется уравнение Эйлера.

Вычислим

теперь вариацию функционала V[ y] . Зададим

приращение

h(x) и

рассмотрим функцию переменной

t :

B[y+th]

V [y +th]= ∫ F(x, y +th, y

′

+th ) dx .

Вычислим ее производную по t:

V [y

+th]=

B[y+th]

B[y +th].

∫

′

Fy h

+ Fy′h dx

+ F (B[y +th], y(B) +th(B), y (B) +th (B))

B[y + th]

Положим

= 0 , тогда y +th = y(x) ,

t =0 = x1 , а вариация функционала

V[ y] равна

δV =

V [y + th]

t=0 = x∫1 [Fy (x, y, y′)h + Fy′ (x, y, y′)h′]dx + F(x1 , y(x1 ), y′(x1 ))

B[y + th]

t =0 .

Интегрируя второй член в подынтегральном выражении по частям, используя

граничное

условие

на

левом

конце

h(a) = 0

равенство

′

Fy (x, y, y ) −

Fy′ (x, y, y ) h dx = 0 , являющееся

следствием

уравнения

Эйлера,

∫a

получим выражение для вариации и приравняем его нулю:

δV = Fy′ (x1 , y(x1 ), y′(x1 ))h(x1 ) + F(x1 , y(x1 ), y′(x1 ))	dB	= 0 .
	dt	t=0
Обозначим B[y + t h]= B(t) и заметим, что B(0) = x1 . По определению B(t) имеем

y (B(t))+t h (B(t))≡ϕ (B(t)), так как абсцисса точки пересечения кривой, записанной в

левой части, с кривой y =ϕ(x)

есть B(t) . Продифференцируем записанное тождество по

t и получим

′

y (B(t))B (t)

+ t h (B(t))B (t) + h(B(t))

= ϕ (B(t))B (t) ,

откуда

h(B(t))

′

B (t) =

′

ϕ (B(t))− y (B(t))−t h

(B(t))

Рассмотрим два случая:

1) Если ϕ′(x1 ) ≠ y′(x1 ) ,

т.е. ϕ′(B(t))− y′(B(t))

t=0 ≠ 0 , то можно выполнить предельный

переход при t → 0 :

h(x1 )

′

= ϕ′(x1 )− y′(x1 ).

B (0)

В этом случае выражение для вариации примет вид

δV = Fy′

x=x

+ F

x=x1

h(x1 ) = 0 .

ϕ′(x1 )− y′(x1 )

Учитывая, что h(x1 ) – произвольное число, и сокращая на h(x1 ) , получаем

(F − ( y′−ϕ′)Fy′ )x=x1 = 0 ,

т.е. условие трансверсальности, сформулированное в теореме.

′		′		′
2) Если ϕ (x		) = y (x		) , то B (t) →∞ . В этом случае равенство нулю вариации
	1		1		t→0
					δV = Fy′ h + F	dB
						dB	= 0
						dt	= 0
						dt	t =0

возможно тогда и только тогда, если F (x1 , y(x1 ), y′(x1 ))= 0 . Легко видеть, что это и есть

условие трансверсальности в случае ϕ′(x1 ) = y′(x1 ) . Теорема доказана. Рассмотрим важный частный случай – задачу со свободным правым концом.

B(t) = b , т.е. левый конец закреплен,

Пусть

а правый может перемещаться по

прямой

x = b

(см. рисунок). В этом случае мы не можем ввести функцию ϕ(x) , т.к.

уравнение границы

x = b . Понятно, что

= 0 . Повторяя рассуждения, приведшие нас

t =0

к получению вариации в предыдущей теореме, имеем

δV = Fy′ h(b) = 0 .

Отсюда

Fy′

= 0

- граничное условие в случае, когда правый конец свободен.

x=b

Рассмотрим теперь случай, когда функционал имеет вид

B[ y]

′

V [y]= ∫ A(x, y)

dx ,

1+( y )

по x, y . В частности, если A ≡1, то

где функция

A(x, y) ≠ 0 и дифференцируема

функционал V [y] определяет длину кривой.

Условие трансверсальности в этом случае

переходит в условие ортогональности кривых y = y(x)

к y =ϕ(x) .

В самом деле,

A(x1 , y(x1 )) 1 + ( y′(x1 ))2 − (y′(x1 ) −ϕ′(x1 ))A(x1 , y(x1 )) y′(x1 ) = 0 .

1 + ( y′(x1 ))2

Приводя к общему знаменателю и сокращая на ненулевые множители, имеем

1 +ϕ′( x1) y′( x1) = 0 ,

откуда

y′(x1 ) = −ϕ′(1x1 ) ,

т.е. условие ортогональности.

Если рассматривать задачу с подвижной границей, в которой правый конец закреплен, а левый – подвижен, то получим тот же результат, только с условием трансверсальности на левом конце.

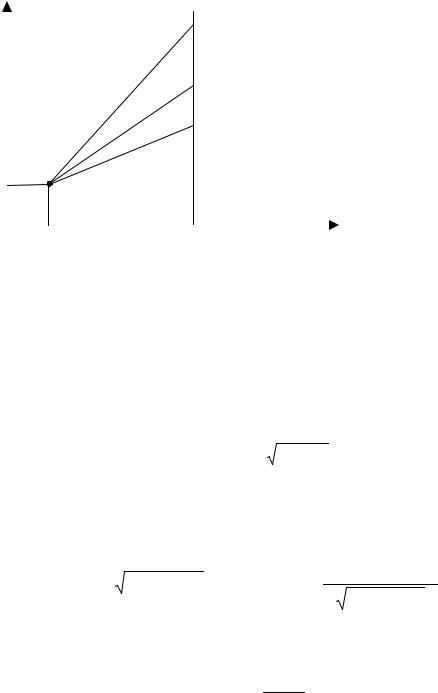
Теперь рассмотрим задачу, в которой оба конца являются подвижными: пусть левый конец функции, на которой осуществляется экстремум функционал V[ y] , может

перемещаться вдоль кривой y =ϕ1 (x) , а правый конец вдоль кривой y =ϕ2 (x) (см.

рисунок). В этом случае должны выполнятся условия трансверсальности на правом и на левом концах.

y(x)

ϕ2(x)

ϕ1(x)

Действительно, если функция y(x) такова, что на ней реализуется экстремум в

классе функций, когда оба конца подвижны, то на ней реализуется экстремум и в классе функций, когда левый конец «правильно» закреплен, а правый подвижен. Из этого следует, что выполняется условие трансверсальности на правом конце (аналогичное утверждение справедливо и для левого конца). Очевидно (см. доказательство теоремы), что функция, на которой достигается экстремум, удовлетворяет уравнению Эйлера.

В заключение параграфа рассмотрим пример. Пусть требуется найти экстремум функционала

x1	′	2
V [y]= ∫	1+( y )		dx
V [y]= ∫	y		dx
0	y

при условии, что левый конец закреплен, а правый может перемещаться вдоль заданной

прямой, т.е. y(0) = 0 ,	y1 = x1 −5 .
Запишем первый интеграл уравнения Эйлера
					′
			F − y Fy′ = C ,
или
			′ 2				y′
		1+( y )		− y′			y′			= C ,
		y		− y′				′ 2		= C ,
						y 1+( y )
или
		1 = C y 1+						′ 2	.
		1 = C y 1+					( y )		.	~
Введем параметр t , полагая										~
Введем параметр t , полагая			y′ = tg t . Тогда y = C1 cos t , и для определения x(t)
запишем					C1 sin t dt
	dx = dy = −				C1 sin t dt			= −C		cos t ,
	dx = dy = −							= −C		cos t ,
		y′			tg t				1
		y′			tg t
откуда				~			~
				~			~
			x = −C1 sin t				+C2 .

<<< < Предыдущая 1 2 3 4 5 6 78 / 108 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.03.2016246.52 Кб3239 Региональное управление и территориальное планирование.pdf
#
17.05.2015361.94 Кб15399885.rtf
#
19.11.201881.41 Кб339_-_texty_-_B-C.doc
#
06.11.2018491.52 Кб23_kl.doc
#
17.05.201534.93 Кб313_referat_MYu.docx
#
18.03.20161.23 Mб733курс, VIсем.Волков,Ягола инт ур.pdf
#
18.03.20161.24 Mб333курс,VIсем Задачи инт ур..pdf
#
18.03.201689.8 Кб264 курс л.р 1.ТСП теор случ процессов.docx
#
18.03.20161.14 Mб1994 курс ЧМ брошюра.docx
#
17.05.2015279.52 Кб64 лихачев.rtf
#
13.08.201940.79 Кб114 раздел.тема1.docx