Министерство образования Российской Федерации

Башкирский государственный университет

Г.Я.Галеева, Л.Е.Маликова, А.Р.Фазылов

Численные методы

Учебное пособие

Уфа

РИО БашГУ

2013

Печатается по решению кафедры вычислительной математики от 30.08.2012г.

Данное учебное пособие предназначено для проведения практических занятий по курсам «Введение в численные методы» и «Численные методы».

В них излагаются численные методы решения трансцендентных уравнений, интегрирования функций, решения систем линейных алгебраических уравнений, аппроксимации и интерполяции функций.

Учебное пособие предназначено для студентов 3 и 4 курсов математического факультета.

Составители:

Доцент кафедры вычислительной математики БашГУ, к.ф.-м.н. Галеева Г.Я.

Старший преподаватель кафедры вычислительной математики БашГУ Маликова Л.Е.

Доцент кафедры вычислительной математики БашГУ, к.ф.-м.н. Фазылов А.Р.

Решение трансцендентных и алгебраических уравнений

Трансцендентное уравнение - это уравнение, содержащее трансцендентные функции (показательные, логарифмические, тригонометрические и обратные тригонометрическим) от неизвестного (переменного).

Например, уравнение

.

Алгебраическим уравнением степени n, в свою очередь, называется уравнение вида

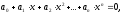
где 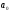, ...,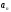- некоторые вещественные числа, причем.

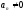Трансцендентные и алгебраические уравнения, в общем случае, можно решать только приближенно. Поэтому особое значение приобретают способы приближенного нахождения корней уравнения и оценки степени их точности.

Постановка задачи

Пусть дано уравнение 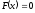, где функцияF(x)определена и непрерывна в некотором конечном или бесконечном интервалеa<x<b.

Если в дальнейшем потребуется существование и непрерывность первой производной 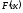или второй производной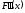, то данные требования будут также оговорены.

Мы будем предполагать, что уравнение 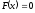имеет лишь изолированные корни, т.е. для каждого корня уравнения существует некоторая окрестность, не содержащая других корней уравнения.

Приближенное нахождение изолированных действительных корней состоит из двух этапов:

1. Отделение корней, т.е. установление по возможности малых промежутков 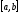, в каждом из которых содержится один и только один корень уравнения.

2. Уточнение приближенного корня, т.е. его определение с заданной точностью.

Для первого этапа рекомендуется применять следующую теорему из математического анализа:

Теорема. Если непрерывная функция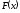принимает значения разных знаков на концах отрезка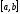, т.е.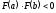, то внутри этого отрезка содержится, по крайней мере, один корень уравнения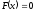, т.е.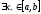, такой что.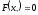

Примечание. Корень 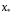будет единственным, если производнаясуществует и сохраняет постоянный знак внутри интервала.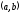

Следовательно, первый этап заключается в определении отрезка 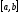, на концах которого функция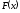 имеет значения разных знаков¹. Для выполнения первого этапа применяют либо графический способ, либо перебор точек разбиения отрезка. Построение графика функции является, в общем случае, не самым эффективным способом для выполнения первого этапа, т.к. данный процесс сам представляет собой достаточно сложную задачу. Его применяют на компьютерах, если для построения графика функций используется или известный профессиональный пакет программ (типа Grapher), или специально разработанная «самодельная» программа. Второй способ - перебор точек - заключается в следующем. 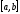Берут достаточно большой отрезок, разбивают его на несколько (например, порядка 10) частей. Вычисляют значения функции во всех точках разбиения. В качестве предварительного решения берут тот отрезок, на концах которого функция имеет разные знаки.

Пример. Нижеприведенная программа находит отрезок, на котором уравнение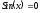имеет изолированный корень.

Program Perebor;

Const N=10; {На сколько частей разбить отрезок}

Var A,B,x1,x2,h:Real; i:Integer;

Function F(X:real):real;

begin

{Задаем функцию уравнения}

F:=Sin(x);

end;

begin {Начало программы}

Writeln(’Введите координаты отрезка A,B’);

Readln(A,B);

{Вычисляем длину частичного отрезка}

h:=(B-A)/N;

{Разбиваем отрезок на N частей}

For i:=1 to N do

begin

{Левая координата отрезка}

x1:=A+h*(i-1);

{Правая координата отрезка}

x2:=A+h*i;

{Если на границах отрезка значения}

{разных знаков, то сообщаем о}

{найденном изолированном корне}

If F(x1)*F(x2)<=0 then

Writeln(’ На отрезке от ’,x1:12:7,

’ до ’,x2:12:7,

’ есть корень’);

end;

{Задержка окна результатов на экране}

Readln;

end.

Также на первом этапе рекомендуется проверить, что в найденном отрезке находится только один изолированный корень. Для алгебраических уравнений можно использовать следующую теорему.

Основная теорема алгебры.Алгебраическое уравнение степениnимеет ровноnкорней, действительных или комплексных, при условии, что каждый корень считается столько раз, какова его кратность.

Поэтому, если для алгебраического уравнения мы нашли nотрезков, на которых функция меняет знак, то мы изолировали все корни.

Для выполнения второго этапа - нахождения изолированного корня с заданной точностью - применяют специальные методы вычислительной математики. Данные методы можно условно разбить на две группы - первые получают решение в виде предела последовательности отрезков, содержащих изолированный корень. Ниже представлены два подобных метода - метод половинного деления и метод хорд. Вторые представляют корень уравнения в виде предела последовательности приближенных корней разной (увеличивающейся) степени точности. Примеры методов - метод итераций, метод Ньютона, модифицированный метод Ньютона и метод секущих.

Необходимо также отметить, что большинство из приведенных методов работают только для корней кратности 1. Если на отрезке существует корень кратности 2 или большей, то для их нахождения следует использовать метод Ньютона с параметром.