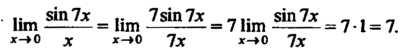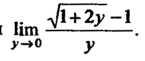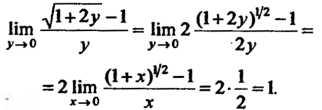- •9) Производная. Геометрический и физический смысл производной
- •10) Производные некоторых основных элементарных функций
- •11) Основные правила дифференцирования
- •12 Таблица основных формул дифференцирования
- •Производные высших порядков
- •13) Основные теоремы дифференциального исчисления
- •15) Правило Лопиталя—Бернулли
- •Доказательство Отношение бесконечно малых
- •Отношение бесконечно больших
- •Примеры
|
8) Некоторые важные пределы |
|
|
|
|
Если угол а выражен в радианах, то При нахождении многих пределов применяются следующие пределы: (13.19) (13.20)
Частными случаями формул (13.19) и (13.20) являются соответственно формулы: (13.22)
При
нахождении пределов вида В виду следующее: 1)
если существуют конечные пределы 2)
если
3)
если
Пример 13.12. Найти При Вида С
использованием формул (13.13) и (13.18),
находим В
частности, при Пример
13.13. Найти Разделив
числитель и знаменатель на
Пример
13.14. Найти
Пример
13.15. Найти Преобразуя
данную функцию, вводя новую переменную Формулу (13.21), находим
|
9) Производная. Геометрический и физический смысл производной
Перейти к списку задач и тестов по теме "Производная. Геометрический и физический смысл производной"
Определение: Производной
функции f(x) (f'(x0))
в точке x0 называется
число, к которому стремится разностное
отношение ![]() ,
стремящемся к нулю.
,
стремящемся к нулю.
Производные элементарных функций.

Правила дифференцирования.
Если у функций f(x) и g(x) существуют производные, то
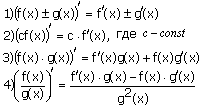
Производная сложной функции:
![]()
Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке

Уравнение касательной к графику функции y=f(x) в точке x0 :
![]()
Физический смысл производной.
Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:
![]()
10) Производные некоторых основных элементарных функций
В
этом пункте мы найдем производные следующих
основных элементарных функций:
постоянной (константы) ![]() степенной функции
степенной функции ![]() с
натуральным
показателем
с
натуральным
показателем ![]() , показательной функции
, показательной функции ![]() логарифмической функции
логарифмической функции ![]() и тригонометрических функций
и тригонометрических функций ![]() .
.
Производные
остальных основных элементарных функций будут
найдены в последующих
пунктах.
1. Производная постоянной ![]() Так
как функция
Так
как функция ![]() сохраняет
постоянное значение на всей числовой оси,
то в произвольно выбранной
точке
сохраняет
постоянное значение на всей числовой оси,
то в произвольно выбранной
точке ![]() любому приращению аргумента
любому приращению аргумента ![]() соответствует приращение функции
соответствует приращение функции ![]() ,
равное нулю. Поэтому
,
равное нулю. Поэтому
![]()
Итак,
![]()
2. Производная степенной функции ![]() с
натуральным показателем
с
натуральным показателем ![]() .
Пусть х — произвольно выбранная
точка,
.
Пусть х — произвольно выбранная
точка, ![]() -приращение
аргумента в этой точке и
-приращение
аргумента в этой точке и ![]() —
соответствующее приращение данной
функции. Тогда по формуле бинома Ньютона
—
соответствующее приращение данной
функции. Тогда по формуле бинома Ньютона
![]()
или
![]()
Следовательно,

Таким образом,
![]()
3. Производная показательной функции ![]() Давая
приращение
Давая
приращение ![]() произвольно
выбранному значению аргумента
произвольно
выбранному значению аргумента ![]() получим
следующее приращение показательной
функции:
получим
следующее приращение показательной
функции:
![]()
Следовательно,
![]()
так
как ![]() (см.
гл. V, § 2, п. 2, пример 3).
(см.
гл. V, § 2, п. 2, пример 3).
Таким образом,
![]()
В
частности, при ![]() получим
получим
![]()
так
как ![]()
4. Производная логарифмической
функции ![]() Возьмем
любое значение
Возьмем
любое значение ![]() из
области определениялогарифмической функции и
дадим ему приращение
из
области определениялогарифмической функции и
дадим ему приращение ![]() Тогда приращение функции
Тогда приращение функции
![]()
Поэтому

Для того чтобы найти этот предел, сделаем следующее преобразование:
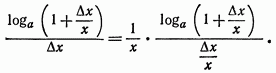
Принимая
во внимание, что величина ![]() постоянна
и что при
постоянна
и что при ![]() также
и
также
и ![]() по
формуле (25) гл. V, § 2 получим
по
формуле (25) гл. V, § 2 получим
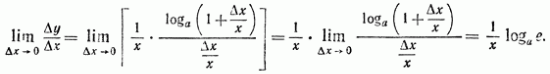
Итак,
![]() (19)
(19)
или
![]()
так как
![]()
В
частности, при ![]() получим
получим
![]()
так
как ![]()
5. Производные функций ![]() Пусть
Пусть ![]() —
приращение произвольно выбранного
значения аргумента
—
приращение произвольно выбранного
значения аргумента ![]() функции
функции ![]() Тогда
приращение этой функции
Тогда
приращение этой функции
![]()
Следовательно,
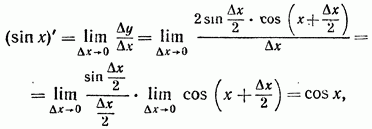
так как по формуле (18) гл. V, § 1, п. 7

Таким образом,
![]()
Аналогично
выводится формула для производной функции ![]()
![]()
11) Основные правила дифференцирования
Установим правила, по которым можно было бы находить производные суммы, произведения и частного функций, зная производные слагаемых, сомножителей, делимого и делителя.
Эти правила мы сформулируем в следующих теоремах.
Теорема
I. Если функции ![]() дифференцируемы
в данной точке
дифференцируемы
в данной точке ![]() ,
то в той же точке дифференцируема и их
сумма, причем производная суммы равна
сумме производных слагаемых:
,
то в той же точке дифференцируема и их
сумма, причем производная суммы равна
сумме производных слагаемых:
![]()
Доказательство.
Рассмотрим функцию ![]() .
Приращению
.
Приращению ![]() аргумента
аргумента ![]() соответствуют
приращения
соответствуют
приращения
![]()
функций и и и. Тогда функция у получит приращение
![]()
Следовательно,
![]()
Так как по предложению функции и и v дифференцируемы, то
![]()
и,
следовательно, ![]() .
.
Итак,
![]()
Замечание. Формула (23) легко обобщается на случай любого конечного числа слагаемых:
![]()
Пример
1. Найти производную функции ![]() Решение.
Применяя вначале формулу (24), а затем
формулы (16), (21) и (20), получим
Решение.
Применяя вначале формулу (24), а затем
формулы (16), (21) и (20), получим
![]()
Теорема
2. Если функции и ![]() дифференцируемы
в данной точке
дифференцируемы
в данной точке ![]() ,
то в той же точке дифференцируемо и их
произведение. При
этом производная произведения находится
по следующей формуле:
,
то в той же точке дифференцируемо и их
произведение. При
этом производная произведения находится
по следующей формуле:
![]()
Доказательство.
Пусть ![]()
Если ![]() получит
приращение
получит
приращение ![]() то
функции и, v и у будут иметь соответственно
некоторые приращения
то
функции и, v и у будут иметь соответственно
некоторые приращения ![]() причем
причем
![]()
Следовательно,
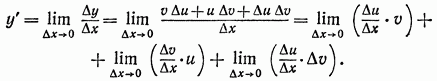
Так
как при фиксированном ![]() постоянны,
то их можно вынести за знак предела.
Поэтому
постоянны,
то их можно вынести за знак предела.
Поэтому
![]()
Кроме того,
![]()
так
как функция v по условию дифференцируема,
а следовательно, и непрерывна, и поэтому ![]()
Таким образом,
![]()
Следствие. Постоянный множитель можно вынести за знак производной:
![]()
Действительно,
если ![]() (с
— постоянная), то по формуле (25)
(с
— постоянная), то по формуле (25)
![]()
В
частности, можно выносить за знак
производной множитель, равный —1, что
равносильно вынесению за знак производной
знака ![]()
![]()
На этом основании можно получить формулу для производной разности двух функций:
![]()
Пример
2. Найти производную функции ![]() .
.
Решение. По формулам (25), (18) и (22) получим
![]()
Пример
3. Найти производную многочлена ![]() Решение.
Применяя последовательно формулы (24),
(26), (16) и (15), получим
Решение.
Применяя последовательно формулы (24),
(26), (16) и (15), получим
![]()
Замечание.
Формулу (25) можно обобщить на случай
любого конечного числа ![]() сомножителей.
Если, например,
сомножителей.
Если, например, ![]() ,
то
,
то
![]()
В самом деле,
![]()
Теорема
3. Если в данной точке ![]() функции
функции ![]() дифференцируемы
и
дифференцируемы
и ![]() ,
то в той
,
то в той ![]() точке
дифференцируемо и их частное
точке
дифференцируемо и их частное ![]() причем
причем
![]()
Доказательство.
Пусть ![]() — приращение аргумента
— приращение аргумента ![]() а
а ![]() —
соответствующие приращения функций
—
соответствующие приращения функций ![]() .
Тогда функция
.
Тогда функция ![]() будет
иметь приращение
будет
иметь приращение
![]()
Следовательно,

или
![]()
Мы
считали, что ![]() вследствие
предположения о дифференцируемости, а
следовательно, инепрерывности функции у.
вследствие
предположения о дифференцируемости, а
следовательно, инепрерывности функции у.
Пример
4. Найти производную функции ![]() .
.
Решение. Представив данную функцию в виде частного
![]()
получим по формуле (29):
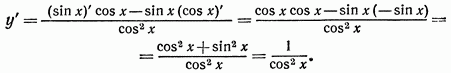
Таким образом,
![]()
При
этом условие ![]() выполняется
для любого
выполняется
для любого ![]() принадлежащего
области определения функции
принадлежащего
области определения функции ![]()
Аналогично
выводится формула для производной функции ![]() :
:
![]()

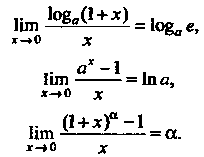 (13.21)
(13.21)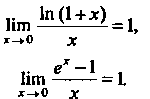 (13.23)
(13.23)