Лабораторна робота № 4

Тема: Розробка алгоритму і програми мінімізації функцій алгебри логіки методом Квайна.

Мета: Набути навиків мінімізації логічних функцій методом Квайна.

Теоретичні відомості Метод Квайна

При мінімізації по методу Квайна (базис 1) передбачається, що початкова функція задана в ДДНФ.

Імпліканта функції – деяка логічна функція, яка перетворюється в нуль при наборі змінних, на якому сама функція також рівна нулю.

Тому будь-який кон'юнктивний терм, що входить до складу СНДФ або група термів, сполучених знаками диз'юнкції, є імплікантами початкової НДФ.

Первинна імпліканта функції – імпліканта типу елементарної кон'юнкції деяких змінних, жодна частина якої вже не є імплікантою.

Завдання мінімізації по методу Квайна полягає в попарному порівнянні всіх імплікант, які входять в ДДНФ, з метою виявлення можливості поглинання якоїсь змінної:

(правило 1)

Таким чином, вдається знизити ранг термів. Ця процедура проводиться до тих пір, поки не залишиться жодного члена, що допускає поглинання з яким-небудь іншим термом. Терми, які підлягли поглинанню, наголошуються. Невідмічені терми представляють собою первинні імпліканти.

Отриманий логічний вираз не завжди виявляється мінімальним. Тому досліджується можливість подальшого спрощення. Для цього складається таблиця, в рядках якої записуються знайдені первинні імпліканти, а в стовпцях вказуються терми початкового рівняння. Клітки цієї таблиці відмічаються у випадку, якщо первинна імпліканта входить до складу якого-небудь терму. Після цього завдання спрощення зводиться до того, щоб знайти таку мінімальну кількість первинних імплікант, які покривають всі стовпці.

Приклад виконання

Метод Квайна виконується у декілька етапів, розглянемо його застосування на конкретному прикладі.

Хай необхідно мінімізувати логічну функцію, задану у вигляді

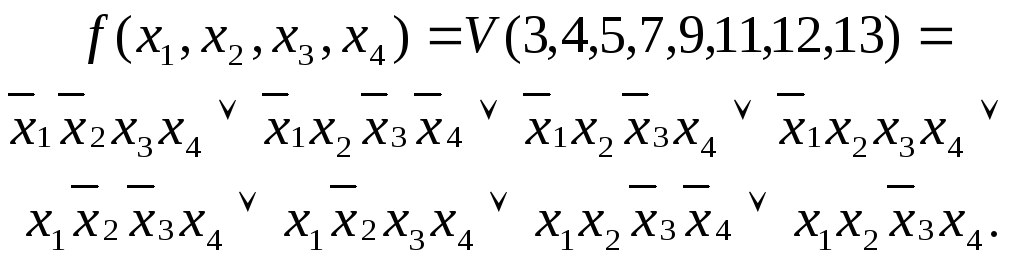
Завдання розв'язується у декілька етапів.

Етап 1. Знаходження первинних імплікант. Перш за все складається таблиця (табл. 1) і знаходяться імпліканти четвертого і третього рангу, тобто знижується ранг членів, що входять в СНДФ.

Потім складається інша таблиця (табл. 2), яка включає всі терми, що не піддалися поглинанню, а також первинні імпліканти третього рангу. Складання таблиць продовжується до тих пір, поки не можна буде застосувати (правило 1). У даному прикладі можна дійти до первинної імпліканти другого рангу (табл. 2) – .

Первинні імпліканти якнайменшого рангу виділені в табл. 2.

Етап 2. Розстановка міток. Складається таблиця, число рядків якої рівне числу одержаних первинних імплікант, а число стовпців співпадає з числом мінтермів СНДФ. Якщо в деякий мінтерм СНДФ входить яка-небудь з первинних імплікант, то на перетині відповідного стовпця і рядка ставиться мітка (табл. 3).

Етап 3. Знаходження істотних імплікант. Якщо в якому-небудь із стовпців табл. 3 є тільки одна мітка, то первинна імпліканта у відповідному рядку є суттєвою, оскільки без неї не буде одержано всю безліч заданих мінтермів. У табл. 3 істотною імплікантою є терм . Стовпці, відповідні істотним імплікантам, з таблиці викреслюються.

Етап 4. Викреслювання зайвих стовпців. Після третього етапу в результаті викреслювання стовпців 2, 3, 7 і 8 виходить табл. 4. Якщо в таблиці є два стовпці, в яких є мітки в однакових рядках, то один з них викреслюється. Покриття стовпця, який залишився, здійснюватиме відкинутий мінтерм. У прикладі такого випадку немає.

Етап 5. Викреслювання зайвих первинних імплікант. Якщо після відкидання деяких стовпців на етапі 4 в табл. 4 з'являються Рядки, в яких немає жодної мітки, то первинні імпліканти, відповідні цим рядкам, виключаються з подальшого розгляду, оскільки вони не покривають мінтерми, шо залишилися в розгляді.

Етап 6. Вибір мінімального покриття. Вибирається в табл. 4 така сукупність первинних імплікант, яка включає мітки у всіх стовпцях принаймні по одній мітці в кожному стовпці. При декількох можливих варіантах такого вибору віддається перевага варіанту покриття з мінімальним сумарним числом букв в імплікантах, створюючих покриття. Цій вимозі задовольняють первинні імпліканти і .

Таким чином, мінімальна форма заданої функції складається з суми істотних імплікант (етап 3) і первинних імплікант, які покривають мінтерми, що залишилися (етап 6):

.