
Курсовая_ИНФОРМАТИКА (МАШ, КТО, ПТМК)-2015
.pdf
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Брянский государственный технический университет
Утверждаю Ректор университета
__________________А.В.Лагерев
«____»____________2011 г.
ИНФОРМАТИКА
РЕШЕНИЕ ЗАДАЧ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ С ПОМОЩЬЮ ПРОГРАММ EXCEL И MATHCAD
Методические указания к выполнению курсовой работы
для студентов очной формы обучения технических направлений подготовки бакалавров
Брянск 2011

2
УДК 004.67
Информатика. Решение задач вычислительной математики с помощью программ Excel и Mathcad [Электронный ресурс]: методические указания к выполнению курсовой работы для студентов очной формы обучения технических специальностей. – Брянск: БГТУ, 2011. – 64с.
Разработали: М.В.Зернин к.т.н., доц., Д.А.Коростелёв к.т.н., доц., О.Л.Никольский к.т.н., доц.
Рекомендовано кафедрой «Информатика и программное обеспечение» БГТУ (протокол №1 от 31.08.11)
Научный редактор А.А.Азарченков Редактор издательства Л.И.Афонина Компьютерный набор Д.А.Коростелёв
Темплан 2011 г., п.284
__________________________________________________________
Подписано в печать 23.12.11. Формат 60х84 1/16 |
|
Усл.печ.л. 3,72. Уч.-изд.л. 3,72 |
Бесплатно. |
Издательство Брянского государственного технического университета 241035, Брянск, бульвар 50-летия Октября, 7, БГТУ. 58-82-49. Лаборатория оперативной полиграфии БГТУ, ул. Институтская, 16.
3
1. ЦЕЛЬ РАБОТЫ
Целью работы является закрепление и развитие навыков использования программных продуктов Excel и Mathcad для решения некоторых задач вычислительной математики, которые понадобятся в процессе дальнейшего обучения в вузе и в профессиональной деятельности инженера.
2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Курсовая работа состоит из 5 обязательных и нескольких (по желанию студента) дополнительных заданий. Задания необходимо выполнить в программах Excel и Mathcad. Документальным результатом курсовой работы является пояснительная записка, которая оформляется после выполнения заданий, содержит подробное описание всей проделанной работы и сдается на проверку в распечатанном виде преподавателю. После проверки курсовой работы преподавателем студент должен ее защитить. При защите курсовой работы в обязательном порядке должны быть предоставлены исходные файлы (электронные версии) с выполненными заданиями в программах Excel и Mathcad. По итогам защиты курсовой работы преподаватель выставляет студенту оценку по 5-балльной шкале.
При выполнении курсовой работы рекомендуется придерживаться установленного графика (табл. 1). В случае грубого нарушения этого графика, неполного выполнения курсовой работы или выполнения ее с ошибками или же неправильного оформления пояснительной записки оценка за курсовую работу может быть снижена.
|
|
Таблица 1 |
|
График выполнения курсовой работы |
|
№ |
Этап |
Сроки |
1 |
Получение индивидуального варианта с |
До 25 марта текущего |
|
заданиями к курсовой работе |
года |
2 |
Решение задач с использованием программ |
До 1 мая текущего года |
|
Excel и Mathcad |
|
3 |
Оформление пояснительной записки и сдача |
До 15 мая текущего года |
|
ее на проверку |
|
4 |
Защита курсовой работы |
До 31 мая текущего года |
4
3.СОДЕРЖАНИЕ РАБОТЫ
3.1.Исследование нелинейной функции одной переменной
3.1.1.Условие задания № 1
Дана нелинейная функция f(x) и указан диапазон изменения аргумента (прил. 1) согласно варианту. Требуется:
1.Выполнить исследование нелинейного уравнения вида f(x)=0 (отыскать корни и экстремумы) с помощью программ Excel и Mathcad. Для этого необходимо выполнить следующие действия:
Провести табулирование функции f(x) на заданном интервале (прил.1). Шаг табуляции h=0,2. Возможно применение другого шага, если при этом график получается более информативным и наглядным. Оформить таблицу (рамки, названия столбцов и т.п.).
Построить график функции f(x). Нежелательно использовать линии с маркерами, так как иногда наличие маркеров затрудняет определение характерных точек на кривой, например точек пересечения с горизонтальной осью.
По графику определить приближенные значения корней уравнения f(x)=0 и точек экстремума функции. Этот этап называется «локализация корней и экстремумов». На нем необходимо обязательно задавать начальное приближение того значения аргумента, вблизи которого имеется корень или экстремум. В ходе последующего использования имеющихся процедур уточняется значение аргумента (соответствующего нужному корню или экстремуму). Поэтому для каждого корня или экстремума обязательно должно быть задано свое начальное приближение.
С помощью процедуры «Подбор параметра» определить уточненные значения корней уравнения f(x)=0. Точность реализации этого этапа можно настроить, используя меню «Параметры». Результат записать с точностью 5 знаков после запятой.
5
2.С помощью надстройки «Поиск решения» Excel найти экстремумы функции f(x). Выделить в таблице цветом точки корней и экстремумов или привести в соответствующих строках подписи рядом с таблицей («Корень 1», «Корень 2», «Максимум 1», «Минимум 2» и т.п.). Результат записать с точностью 5 знаков после запятой.
3.Решить это же нелинейное уравнение с помощью программы Mathcad. Для этого необходимо выполнить следующие действия:
Построить график функции f(x).
По графику определить начальные приближения корней уравнения f(x).
Для каждого приближения определить уточненные значения корней уравнения. Для этих целей могут быть использованы соответствующие функции Mathcad: «root», «find» и т.п. Результат записать с точностью 5 знаков после запятой.
4.С помощью символьных вычислений в Mathcad найти производную функции f(x). Найти экстремумы функции f(x) путем решения уравнения f'(x)=0 аналогично пункту 3. Результат записать с точностью 5 знаков после запятой.
5.Сравнить полученные результаты и сделать выводы об эффективности Excel и Mathcad при решении задач нахождения корней нелинейного уравнения и поиска экстремумов функции.
3.1.2.Пример выполнения задания № 1
|
Рассмотрим выполнение задания №1 |
на |
|
примере |
уравнения |
|||||
x2 |
1 |
|
5 0 и интервале [-5;5]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x 1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
Выполним табулирование функции x2 |
|
|
1 |
|
5 |
0 |
в Excel на |
||
|
|
|
|
|||||||
x 1
интервале [-5;5] с шагом 0,2.
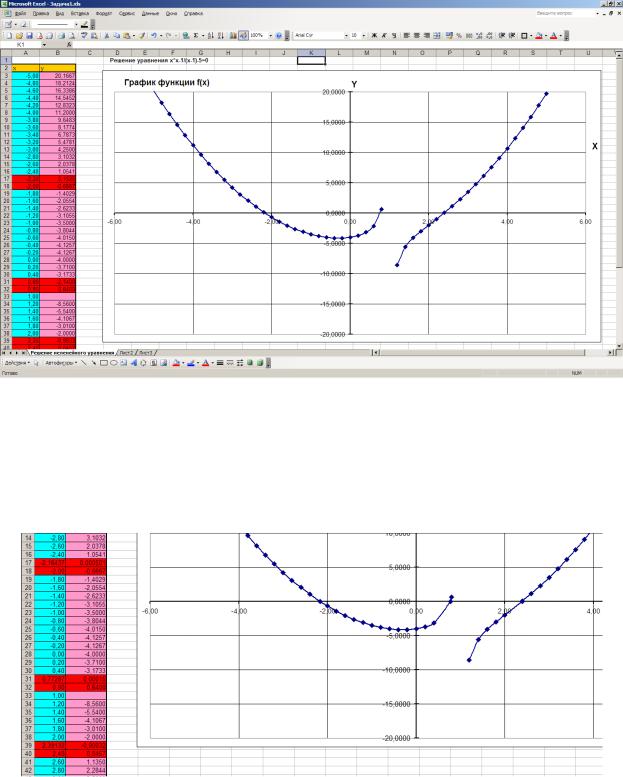
На основе полученной таблицы табуляции строим график функции f(x) (рис. 1).
1.На полученном графике определяем приближенные значения корней уравнения. Данные корни будут находиться в точках пересечения графика функции с осью абсцисс, а также их
6
приближенные значения можно определить по таблице табуляции в строках, где значения в столбце y меняют свой знак. Получаем следующие приближенные значения корней уравнения: -2.0, 0.6 и 2.2.
Рис. 1. Табуляция функции и построение графика в Excel
2.С помощью процедуры «Подбор параметра» определяем точное значение корня для каждого приближенного значения.
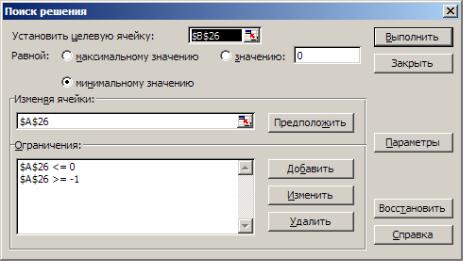
Получаем следующие значения корней уравнения: x1=- 2.16437, x2=0.77287 и x3=2.39132 (рис.2).
Рис. 2. Фрагмент листа Excel с найденными корнями уравнения
7
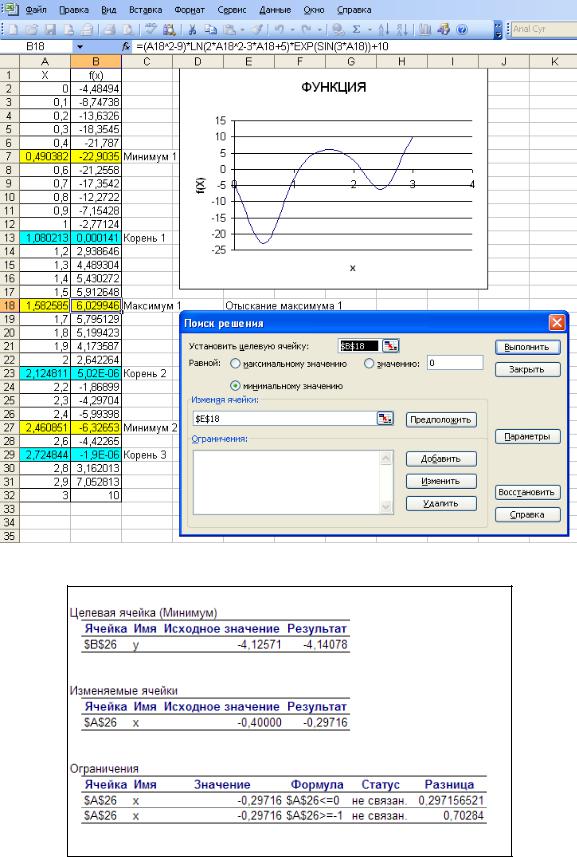
3.Найдем в Excel экстремумы функции f(x). По графику видно, что данная функция имеет только одну точку экстремума (минимума) в районе x=-0,4. Для нахождения этого экстремума воспользуемся надстройкой «Поиск решения» и настроим её согласно рис.3. Для этого сначала устанавливается целевая ячейка (ячейка из столбца значений функций – f(x), в которой функция принимает либо максимальное, либо минимальное значение по сравнению с соседними: верхними и нижними ячейками). После этого в поле «Изменяя ячейки» указывается адрес ячейки, в которой содержится соответствующее значение аргумента x. Именно этот адрес ячейки содержится в формуле для вычисления значения функции в целевой ячейке (обычно изменяемая ячейка расположена слева от целевой ячейки).
Рис. 3. Настройка формы «Поиск решения» для функции с разрывом
Для функций такого типа (с разрывами) обязательно нужно добавлять ограничения нижнего и верхнего значения аргумента, чтобы в решении не оказалось бесконечное число, соответствующее точке разрыва. Для функций без разрыва ограничений можно не задавать (рис.4).
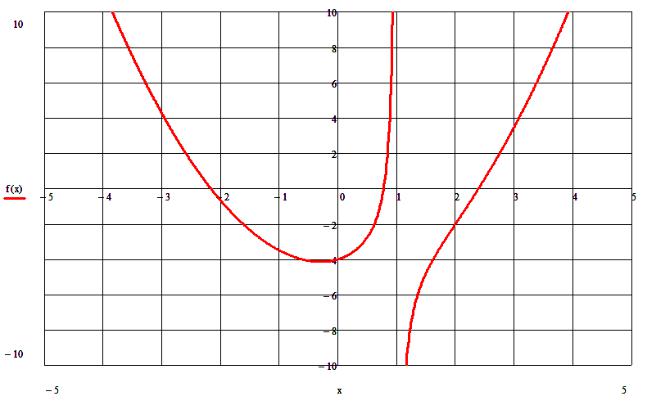
4.Сформируем отчет о результатах поиска (рис. 5), из которого видно, что искомое значение экстремума функции xэкс=-0,29716.
8
Рис. 4. Решение задачи для функции, не имеющей разрывов
Рис. 5. Отчет о результатах поиска экстремума функции с помощью надстройки «Поиск решения»
9
5. С помощью программы Mathcad построим график функции
y x2 |
1 |
|
5 |
на интервале [-5;5] (рис. 6). По графику |
|
|
|
||||
x 1 |
|||||
|
|
|
|||
определяем приближенные значения корней уравнения: -2,1,
0,8 и 2,4.
Рис. 6. График функции f(x), построенный в Mathcad
6.С помощью функции root находим точные значения корней уравнения: x1=-2,16425, x2=0,77287 и x3=2,39138.
7.Используя инструментарий Mathcad для работы с
символьными |
вычислениями, |
находим |
производную |
|
|
1 |
|
|
|
x 1 2 . |
|
|
||
f x 2x |
|
|
||
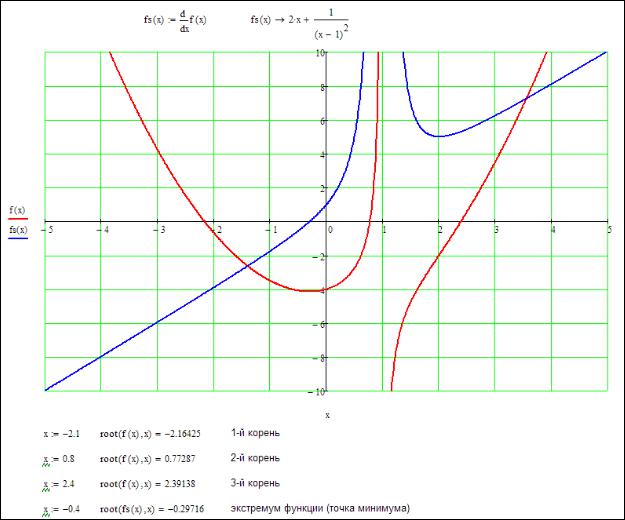
8. Построим график производной функции f(x). По графику определяем приближенное значение корня f'(x)=0: x=-0,4. С помощью функции root находим точное значение корня уравнения f'(x)=0 (рис. 7), а значит, и значение экстремума функции f(x): x=-0,29716.
10
Рис. 7. Нахождение корней уравнения и экстремума функции с помощью Mathcad
3.2. Основные операции с матрицами
Матрицей размерности m n называется прямоугольная таблица m n чисел ai,j (i=1,..,m, j=1,..,n):
a |
a |
... |
a |
|
|
|
|
11 |
12 |
|
1n |
|
|
a21 |
a22 |
... |
a2n |
|
||
A |
... ... ... ... |
|
, |
|||
|
|
|
||||
|
|
|
|
|
||
|
|
am2 |
... |
|
|
|
am1 |
amn |
|
||||
расположенных в m строках и n столбцах. Матрица называется квадратной, если m=n.
Чтобы умножить матрицу на число, нужно умножить на это число все элементы матрицы. Суммой двух матриц одинаковой размерности называется матрица той же размерности, каждый
