
Курсовая_ИНФОРМАТИКА (МАШ, КТО, ПТМК)-2015
.pdf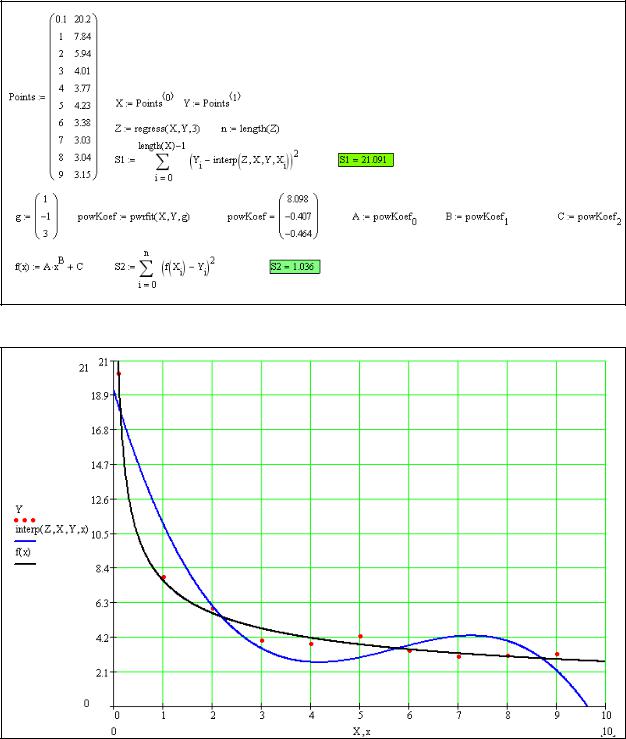
21
6.Построим на одной координатной плоскости графики аппроксимирующих функций (рис. 17).
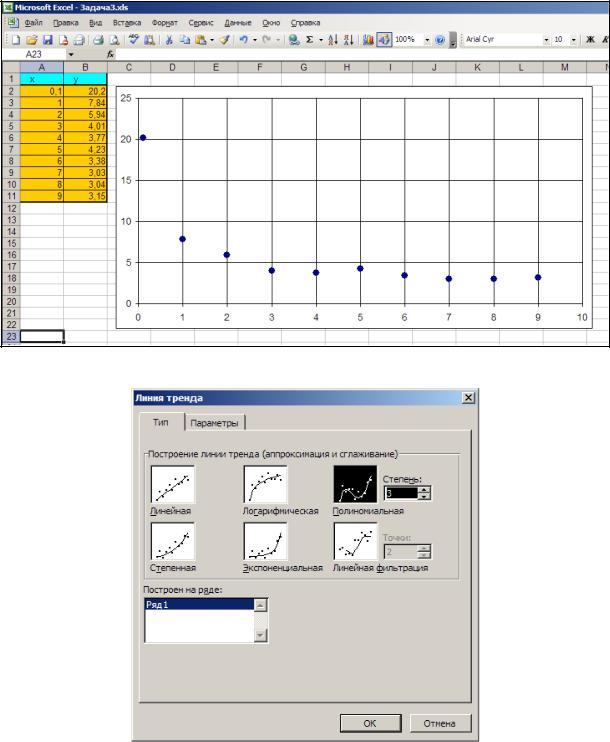
7.Проведем аппроксимацию точек с помощью Excel. Для этого сначала заполним исходную таблицу точек и отметим эти точки на графике (рис. 18).
Рис. 16. Аппроксимация точек в Mathcad
Рис. 17. Графики аппроксимирующих функций
22
Рис. 18. Исходные точки для аппроксимации на графике
Рис. 19. Добавление на график аппроксимирующей линии (линии тренда)
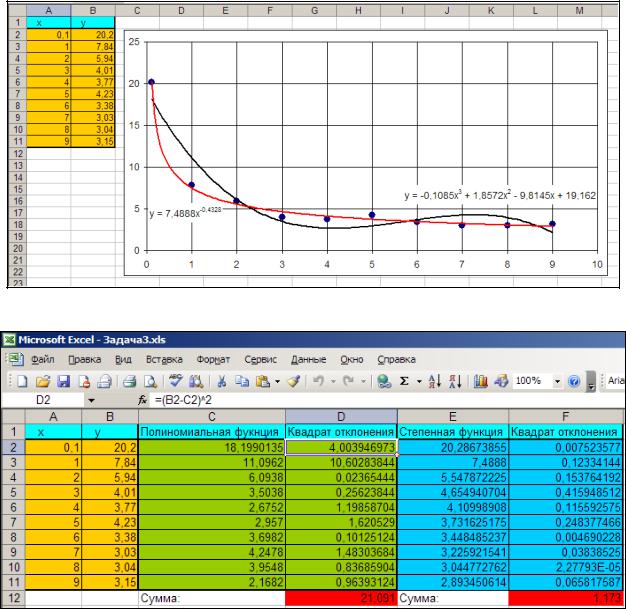
8.Вызовем контекстное меню для одной из точек на графике и выберем пункт «Добавить линию тренда…». Для начала проведем аппроксимацию с помощью полинома 3-й степени.
23
Для этого в открывшемся диалоговом окне «Линия тренда» выберем «Полиномиальная» и укажем степень «3» (рис. 19).
9.Аналогично добавим линию тренда на основе степенной функции. В настройках линий тренда выставим галочку «показывать уравнение на диаграмме». Результат представлен на рис. 20. Получили следующие аппроксимирующие функции.
Для полинома 3-й степени:
y0,1085x3 1,8572x2 9,8145x 19,162 .
Для степенной функции: y 7,4888x 0,4328 .
Рис. 20. Получение графиков функций аппроксимации
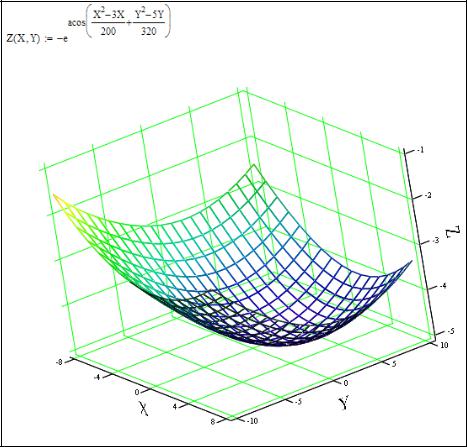
Рис. 21. Расчет в Excel суммы квадратов отклонений для аппроксимирующих функций
24
10.Определим сумму квадратов отклонений для полученных функций в узловых точках (рис. 21):
Для полинома 3-й степени эта величина равна 21,091.
Для степенной функции эта величина равна 1,173. Следовательно, аппроксимация набора данных степенной функцией более точна, чем полиномом 3-ей степени.
3.5.Экстремум функции двух переменных
3.5.1.Условие задания № 5
Найти экстремум функции двух переменных в Excel и Mathcad. Построить график двумерной поверхности в Excel и Mathcad. Сравнить результаты и сделать выводы. Варианты задания приведены в прил.4.
3.5.2. Пример выполнения задания № 5
|
|
2 |
3x |
|
2 |
5 y |
|
|
|
x |
|
y |
|
||
|
arccos |
|
|
|
|
|
|
Для примера рассмотрим функцию z e |
|
200 |
|
320 |
|||
|
|
|
|
|
|
. |
|
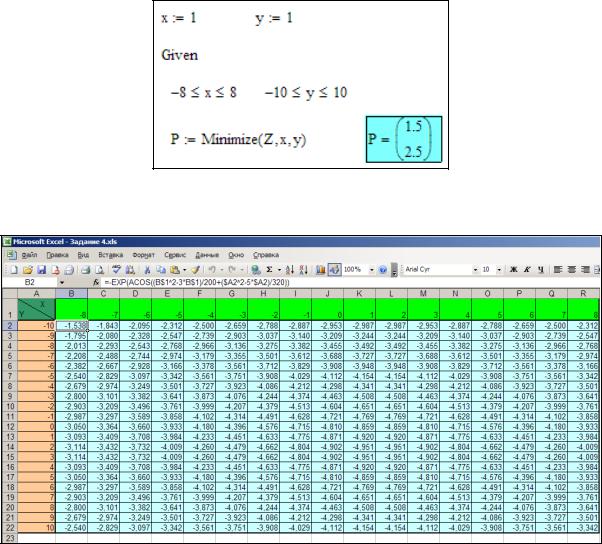
1. Построим график функции в Mathcad (рис. 22).
Рис. 22. Построение поверхности в Mathcad
25
2.По графику определяем, что функция z имеет только один экстремум – точку минимума.
3.Воспользуемся блоком решения Mathcad и функцией Minimize. За начальное приближение точки минимума возьмем x=1 и y=1. В качестве ограничений укажем интервалы для x [-8;8] и y [-10;10].
4.Получили решение x=1,5; y=2,5 (рис. 23).
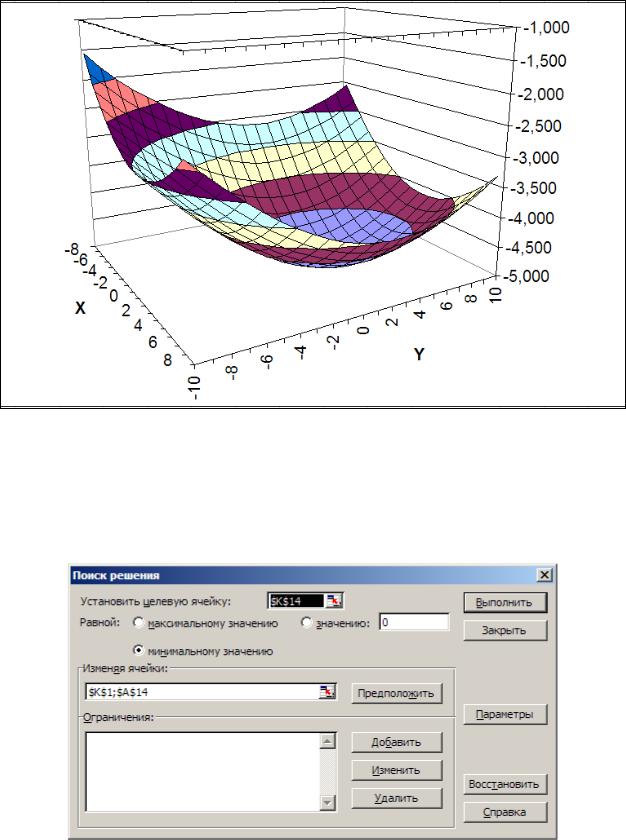
5.Теперь выполним это же задание в Excel. Для этого сначала проведем табуляцию функции на интервале по x [-8;8] и y [-10;10] (рис. 24).
Рис. 23. Минимизация функции в Mathcad
Рис. 24. Табулирование функции 2-х переменных в Excel
6. На основе полученной таблицы строим поверхность (рис. 25).
26
Рис. 25. График функции двух переменных в Excel
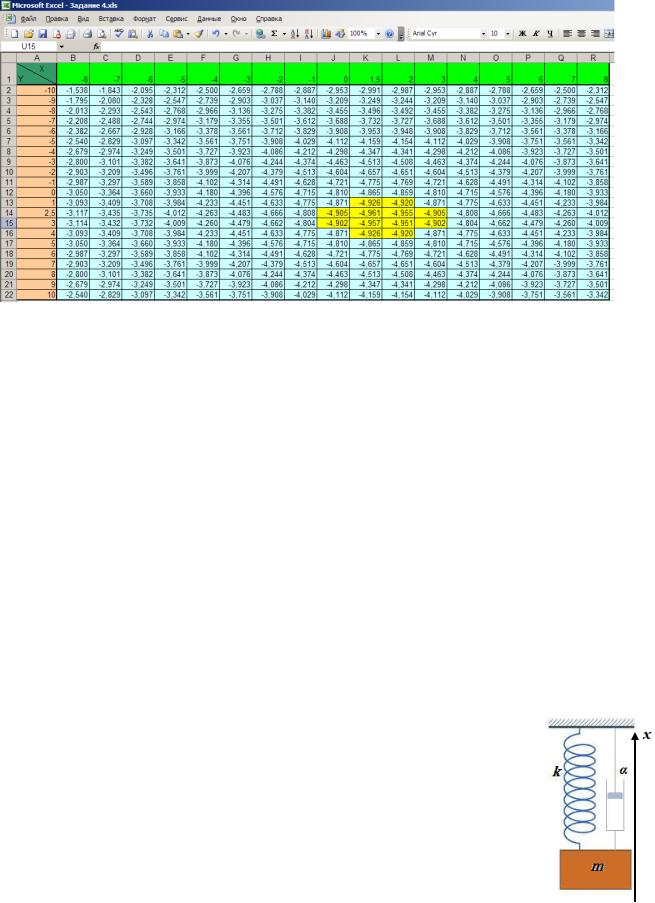
7.С помощью надстройки «Поиск решения» найдем точку минимума. Для этого настроим соответствующее диалоговое окно следующим образом (рис. 26). В результате выполнения получим искомую точку минимума: x=1,5; y=2,5 (рис. 27).
Рис. 26. Настройка формы «Поиск решения» для нахождения минимума функции
двух переменных
27
Рис. 27. Результаты поиска решения с найденными значениями целевой и изменяемой ячеек
3.6. Дополнительные задания
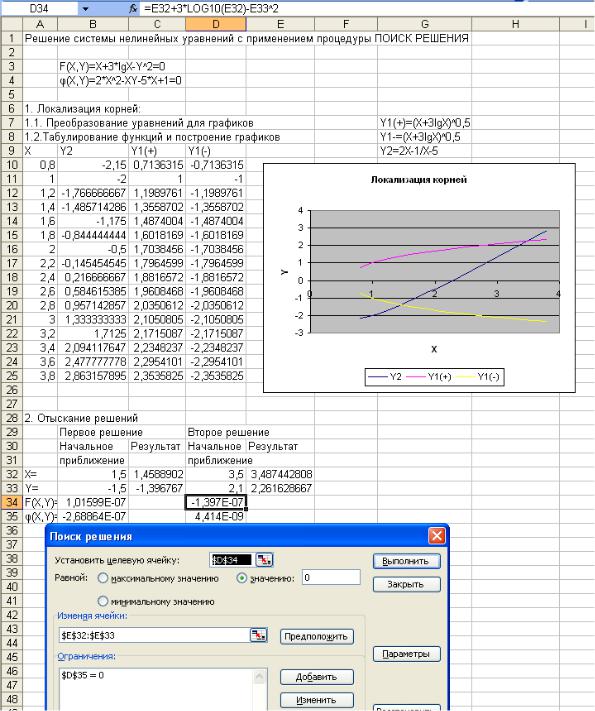
Задания являются необязательными, но их выполнение положительно влияет на итоговую оценку за курсовую работу. Вариант задания студент может выбрать по согласованию с преподавателем только после выполнения пяти обязательных заданий. Варианты заданий приведены в прил.5. В качестве примера приведем задачу отыскания решений системы двух нелинейных уравнений с двумя неизвестными в Excel (рис. 28).
В качестве дополнительного задания может быть взято решение задачи определения параметров затухающего гармонического осциллографа.
3.6.1. Постановка задачи
Проводится физический опыт с подвешенным на пружине (k) грузом (m) и установленным параллельно пружине вязким демпфером (α) – затухающим гармоническим осциллятором. Груз отводится в крайнее верхнее положение и освобождается, после чего совершает свободные колебания, амплитуда которых постепенно уменьшается в результате рассеяния механической энергии в демпфере. Положения груза по вертикали фиксируются
через равные промежутки времени. Цель опыта – оценить (т.е.
|
|
|
28 |
|
|
приблизительно |
определить) |
параметры, |
определяющие |
||
колебательные движения груза - жёсткость |
пружины k |
и |
|||
коэффициент вязкого сопротивления демпфера α. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 28. Пример отыскания решений системы двух нелинейных уравнений с двумя неизвестными
Эти параметры сложнее определить прямыми измерениями в отличие от массы груза, который можно просто взвесить. Подобные

29
задачи (в более сложной постановке) встречаются в инженерной практике и называются задачами идентификации параметров динамических систем, причём в ряде случаев по опытам оцениваются инерционные параметры (массы), если взвесить объёмную конструкцию сложнее, чем прямо замерить жёсткость упругих элементов.
3.6.2.Математическое описание опыта
Воснове математического описания данного опыта лежит следующее дифференциальное уравнение свободного движения массы m на пружине жёсткостью k и коэффициентом вязкого сопротивления α
̈̇
Предполагается, что масса m системы известна по результатам взвешивания, в опыте подлежат оценке значения жёсткости k и коэффициента вязкого сопротивления α. Введём обозначения
, ω02 = . Исходное уравнение примет вид
̈ω02 = 0.
При малом трении (γ < ω0) груз совершает затухающие колебательные движения и решение уравнения выглядит так:
|
|
|
( ) |
( t + φ), |
где |
|
|
- частота свободных колебаний, амплитуда A и фаза φ |
|
√ |
||||
определяются начальными условиями. Если начальное положение груза в опыте принимается таким, как описано, A = 1, φ = . С учётом этого уравнение колебаний груза принимает вид
( ) |
( t ). |
|
|
(*) |
|
По результатам опыта находятся величины |
Исходные |
||||
параметры системы выражаются через γ и ωf по формулам: |
|||||
|
|
|
|
|
|
2 m, |
k m 2 |
2 |
( ) |
||
|
|
f |
|
|
** |
3.6.3. Методика обработки экспериментальных данных |
|||||
Для определения |
значений параметров |
используется |
|||
простейший вариант метода наименьших квадратов (МНК), как одного из наиболее эффективных методов сглаживания (аппроксимации) экспериментально полученных рядов точек, разнообразные модификации которого широко используются для обработки экспериментов в различных областях человеческой
30
деятельности. Исходными данными для математической обработки опыта являются два ряда значений – моменты времени t, в которые замеряются положения груза (момент начала движения груза считается нулевым), и сами эти положения xэкс(t). Последовательность действий следующая:
1. Задают начальные значения ωf и α, приблизительно соответствующие реальным значениям. В качестве начального приближения для ωf можно принять значение 2πfэкс , fэкс – частота затухающих колебаний груза по опыту, Гц (частота прохождения грузом некоторой точки, например, нулевой, на оси координат в одном и том же направлении), которую проще всего приближённо определить, мысленно проанализировав набор экспериментальных точек или построив соответствующий график. Согласно теории, затухающее “периодическое” движение имеет место при γ < ω0, в качестве начального значения можно принять любое в диапазоне
0< γ < 2πfэкс.
2.Рассчитывают по формуле (*) координаты колеблющегося
груза xрасч(t) в те же моменты времени от начала колебаний, когда сделаны экспериментальные замеры xэкс(t). Очевидно, что xрасч зависит также от величин выбранных γ и ωf .
3.Рассчитывают для всего ряда моментов t сумму квадратов
разностей |
( ) ∑ ( ( ) |
( )) , |
которая, очевидно, |
является |
|
функцией |
искомых |
параметров |
. Найденная таким |
образом |
|
сумма квадратов |
разностей |
называется квадратичной |
невязкой |
||
(между экспериментальными и расчётными точками). |
|
||||
4.Используя тот или иной метод вычислительной
математики, |
находят такие значения |
при |
которых невязка |
S , f имеет наименьшую величину в допустимой для аргументов |
|||
области |
значений. Найденные |
значения |
считаются |
наилучшими (оптимальными) с точки зрения максимальной близости экспериментальных и теоретически рассчитанных координат колебаний груза и могут использоваться в дальнейшем компьютерном моделировании.
5.Результатам решения не верим слепо, обязательно проверяем правильность по графикам.
6.Как видно из формул (**), α и k пропорциональны массе m, для простоты в заданиях принимается m = 1.
