
Курсовая_ИНФОРМАТИКА (МАШ, КТО, ПТМК)-2015
.pdf11
элемент которой равен сумме соответствующих элементов слагаемых.
Произведение матриц определяется следующим образом. Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй. Если заданы матрицы A и B:
a |
a |
... |
11 |
12 |
|
a21 |
a22 ... |
|
A |
|
|
... ... ... |
||
|
|
|
|
am2 ... |
|
am1 |
||
a |
|
b |
1n |
11 |
|
a2n |
b21 |
|
... , |
B ... |
|
|
|
|
|
|
|
amn |
bn1 |
|
b |
... |
b |
|
|
12 |
|
1k |
|
|
b22 |
... |
b2k |
|
, |
... ... ... |
|
|||
|
|
|||
|
|
|
|
|
bn2 |
... |
bnk |
|
|
|
|
|||
то произведением матриц A и B называется матрица
c |
c |
... |
c |
|
|
|
|
11 |
12 |
|
1k |
|
|
c21 |
c22 |
... |
c2k |
|
|
|
C |
... |
... ... ... |
|
, |
||
|
|
|
||||
|
|
|
|
|
||
|
|
cm2 |
... |
|
|
|
cm1 |
cmk |
|
||||
элементы которой вычисляются по формуле:
cij ai1b1 j |
ai 2b2 j |
... ainbnj , |
i 1,...,m, j 1,...,k. |
То есть, говоря упрощенным языком, каждый ij-элемент матрицы С является результатом умножения i-й строки матрицы А на j-й столбец матрицы В. Перемножаются попарно соответствующие коэффициенты и выполняется суммирование таких произведений. Произведение матриц A и B обозначается AB или А B , т.е. C=AB.
3.2.1. Условие задания № 2
Даны матрицы A, B и С. Вычислить матрицу D по формуле согласно варианту (прил.2). Задание выполнить в Excel и Mathcad.
3.2.2. Пример выполнения задания № 2
Вычислим значение матрицы D по формуле D A B C 5, где
|
|
|
|
|
|
2 |
9 |
8 |
7 |
|
|
|
|
|
|
|
3 |
3 |
5 |
2 |
|
9 |
3 |
1 |
0 |
|
5 |
1 |
8 |
7 |
|||
|
|
|||||||||||||||
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
A |
1 |
9 |
2 |
5 |
7 |
5 |
1 |
8 |
C |
3 |
4 1 |
4 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 5 |
|
|
|
|
|
|
|
|
|
|
|||||
|
7 |
1 , |
|
8 |
4 |
2 |
1 |
, |
|
2 |
6 |
10 |
1 |
. |
||
С помощью Excel рассчитаем матрицу D (рис. 8).

12
Рис. 8. Вычисление матрицы D в Excel
Операции линейной алгебры в EXEL выполняются в следующей последовательности:
1.Выделяется диапазон ячеек (матрица), в котором будет размещен результат. Также в Excel для обозначения матрицы иногда используется термин – «массив».
2.Применяется нужная процедура из категории «математические»:
«МУМНОЖ» - возвращает произведение матриц (матрицы хранятся в массивах). Результатом является массив с таким же числом строк, как массив №1, и с таким же числом столбцов, как массив №2. Обращаем внимание, что массивы №1 и №2 должны задаваться именно в том порядке (слева направо), как они записаны в формуле. Нарушение этого правила приведет не только к неправильному вычислению коэффициентов результирующей матрицы, но и к получению результирующей матрицы другого размера (кроме случая перемножения квадратных матриц).
«ТРАНСП» - транспортирование матрицы (возвращает вертикальный диапазон ячеек в виде горизонтального и наоборот).
«МОБР» - возвращает обратную матрицу для матрицы, хранящейся в массиве.
«МОПРЕД» - возвращает определитель матрицы (матрица хранится в массиве).
3.После появления в массиве результатов первого значения (соответствующего индексам 1,1) для появления остальных

13
нажать сначала клавишу «F2», а потом сочетание клавиш
«Ctrl» + «Shift» + «Enter».
Пример выполнения нескольких операций перемножения матриц и векторов приведен на рис. 9.
Рис. 9. Примеры перемножения матриц
На рис. 10а приведен пример расчета матрицы D средствами Mathcad. Заполним матрицу коэффициентов системы уравнений и найдем ее решение (рис. 10).
Рис. 10. а) вычисление матрицы D в Mathcad;
б) нахождение решения системы уравнений в Mathcad
14
3.3.Решение системы линейных уравнений
3.3.1.Условие задания № 3
Используя коэффициенты полученной матрицы D, решить систему уравнений. Обратить внимание, что для формирования системы линейных уравнений, подлежащей решению, коэффициенты матрицы D использованы в порядке, отличающемся от их записи непосредственно в матрице D.
3.3.2. Пример решения задания № 3
Например, решим следующую систему линейных уравнений:
D1,4 x1 |
D1,1 x2 |
D1,3 x3 |
D1,2 ; |
|||||
|
|
|
D2,1 x2 |
D2,3 x3 |
D2,2 |
|
||
D2,4 x1 |
; |
|||||||
D x D x |
2 |
D x |
3 |
D |
. |
|||
|
3,4 |
1 |
3,1 |
3,3 |
3,2 |
|
||
1.Запишем систему уравнений, используя коэффициенты из полученной матрицы:
51x1 30x2 29x3 11;5x1 31x2 3x3 65;4x1 14x2 62x3 97.
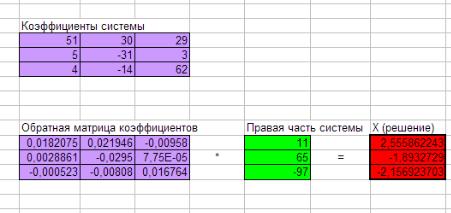
2.Решим полученную систему уравнений в Excel с применением последовательности операций линейной алгебры, а именно – с применением обратной матрицы (рис. 11). В результате получим вектор решения:
|
|
|
2,555862243 |
|
|
|
|
|
|
X |
1,8932729 |
. |
||
|
|
|
|
|
|
|
|
2,156923703 |
|
|
|
|
|
|
Рис. 11. Решение системы линейных уравнений с помощью Excel

15
Еще один пример приведен на рис. 12
Рис. 12. Решение системы линейных алгебраических уравнений с проверками выполнения отдельных шагов
Здесь реализованы несколько проверок: проверка существования решения (вычисление определителя (детерминанта матрицы А); проверка правильности получения обратной матрицы (перемножение исходной матрицы на обратную должно давать единичную матрицу); проверка правильности вычисления искомого вектора (перемножение исходной матрицы на искомый вектор должно давать вектор правых частей). Предпочтительно выполнение задания с матрицей D именно в таком (более полном) объеме со всеми перечисленными проверками.
Реализованная последовательность решения системы уравнений относится к прямым методам, таким как метод Гаусса. Но системы линейных алгебраических уравнений можно решать и

16
итерационными методами, в которых должно быть задано начальное приближение искомого вектора, а процедура решения является уточнением значений коэффициентов этого вектора. Такой метод решения системы уравнения реализован в надстройке «Поиск решения». В этом случае каждое уравнение должно быть записано в одной из ячеек как формула для вычисления правой части. Одна из таких ячеек используется как целевая ячейка (требуем установить в ней истинное значение правой части за счет подбора значений искомого вектора), а другие ячейки с формулами используются как ограничения (требуем установить в них тоже истинные значения правых частей). Пример такого решения приведен на рис. 13.
Рис. 13. Пример решения системы линейных алгебраических уравнений итерационным методом с применением надстройки «Поиск решения»
17
Решение системы уравнений в Mathcad приведено на рис. 10б. В Mathcad также можно при менять прямые (метод Гаусса) и итерационные методы решения систем алгебраических уравнений.
Вкачестве дополнительного задания (задание №6) может быть реализована подобная процедура для заданного варианта системы уравнений с матрицей D (с применением как Excel, так и Mathcad).
3.4.Приближение таблично заданной функции
Винженерной практике довольно часто встречается задача получения зависимости (формулы) между двумя величинами в том случае, когда имеется таблица значений (например, в результате
экспериментальных исследований получены значения величины Yi при некоторых конкретных значениях аргумента Xi, где i=1,2,…m). Но для последующей деятельности требуется формула, связывающая эти две величины, по которой можно было бы с некоторой точностью определить величину Y при любом значении величины X. Получение такой зависимости называется аппроксимацией таблично (точечно) заданной функции.
Частным случаем аппроксимации является интерполяция полиномом (многочленом) n-й степени. Из курса математики известно, что имея m точек, можно получить неизвестные коэффициенты полинома n=m-1 степени. Интерполяцией называется получение такой полиномиальной зависимости Y ( X ) , в соответствии
скоторой для всех пар точек (называемых узлами интерполяции)
имеется совпадение табличных с рассчитанными по зависимости Y ( X ) . Интерполяционная зависимость может быть построена единая для всего интервала определения таблично заданной функции. В этом случае степень полинома на единицу ниже количества несовпадающих узлов интерполяции. Можно построить кусочную интерполяцию, разделив все количество узлов на группы. В пределах каждого такого участка интерполяции получают полином степенью на единицу ниже количества узлов интерполяции в этой группе. Если в группу включать 2 узла, то получается полином первой степени (прямая линия). Такая интерполяция называется кусочно-линейной.
Кроме построения интерполяционных зависимостей, можно строить аппроксимирующие зависимости на основе различных функций взаимосвязи двух рассматриваемых величин. Обычно в этом
18
случае количество неизвестных параметров выбранной функции намного ниже количества пар значений в исходной таблице Y ( X ) . Очевидно, что в этом случае возможно бесконечно большое количество сочетаний конкретных значений параметров аппроксимирующей функции. Необходимо выбирать такие значения параметров, которые в максимальной степени обеспечивали бы близость аппроксимирующей функции к исходным табличным значениям. Обычно применяют критерии квадратичного приближения. А именно, подбирают такие значения параметров аппроксимирующей функции, чтобы сумма квадратов отклонений (разницы вычисленных по ней значений и значений из таблицы) была
минимальной |
m Y ( X i ) Yi ( X i ) 2 |
min . |
Построение |
|
1 |
|
|
аппроксимирующих зависимостей на основе этого принципа (метода наименьших квадратов) реализовано в программах Excel и Mathcad. Точность аппроксимирующих зависимостей разного вида может весьма существенно различаться. В ходе аппроксимации с помощью Mathcad могут быть использованы следующие функции:
«expfit» для определения коэффициентов A, B и C экспоненциальной функции вида C ;
«lnfit» для определения коэффициентов A и B логарифмической функции вида f x A ln x B ;
«pwfit» для определения коэффициентов A, B и C степенной функции вида f x A xB C .
3.4.1.Условие задания № 4
Дана таблично заданная функция - пары точек (xi,yi) (прил. 3), для которых необходимо выполнить следующее.
С помощью программы Mathcad провести кусочно-линейную интерполяцию и найти значения y для следующих значений x:
1,3, 2,6, 4,4, 5,9, 7,1, 8,75. Построить график.
С помощью программы Mathcad провести полиномиальную интерполяцию и найти значения y для следующих значений x: 1,3, 2,6, 4,4, 5,9, 7,1, 8,75. Построить график. Записать уравнение полинома (коэффициенты полинома указать с точностью 10 знаков после запятой).
Провести 2 вида аппроксимации согласно варианту (прил.3). Оба графика построить на одной координатной плоскости. В

19
обоих случаях определить сумму квадратов отклонений для узловых точек. Данное задание выполнить как в Excel, так и в
Mathcad.
3.4.2. Пример выполнения задания № 4
Рассмотрим выполнение данного задания для следующих точек.
x |
0,1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
y |
20,2 |
7,84 |
5,94 |
4,01 |
3,77 |
4,23 |
3,38 |
3,03 |
3,04 |
3,15 |
В качестве видов аппроксимации будем использовать:
полином 3-й степени;
степенную функцию.
Решим все поставленные задачи с использованием Mathcad.
1. Проведем кусочно-линейную интерполяцию с помощью функции «linterp» для заданных точек (xi,yi) и определим значение функции для указанных значений аргумента
(рис. 14).
|
x |
1,3 |
2,6 |
4,4 |
5,9 |
7,1 |
8,75 |
|
|
y |
7,27 |
4,782 |
3,954 |
3,465 |
3,031 |
3,123 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 14. Кусочно-линейная интерполяция в Mathcad
2.Проведем полиномиальную интерполяцию с помощью функции «regress». Учитывая, что задано 10 точек, то

20
полином должен быть 9-й степени. В результате получили полином, представленный на рис. 15. Построим его график, на котором отметим исходные точки (рис. 15). По графику можно убедиться, что полином проходит через все заданные точки.
Рис. 15. Полиномиальная интерполяция в Mathcad
3. |
Используя функцию «polynom», определим для заданных |
||||||||
|
точек значение функции (рис. 15). |
|
|
|
|||||
|
|
x |
1,3 |
2,6 |
4,4 |
5,9 |
7,1 |
8,75 |
|
|
|
y |
7,084 |
4,698 |
4,046 |
3,493 |
3,088 |
1,699 |
|
4. |
Проведем с помощью Mathcad аппроксимацию для заданных |
||||||||
|
точек с помощью полинома 3-й степени и степенной функции |
||||||||
|
(рис. 16). Определим сумму квадратов отклонений для |
||||||||
|
узловых точек (рис. 16): |
|
|
|
|
||||
|
Для полинома 3-й степени эта величина равна 21,091. |
||||||||
|
Для степенной функции эта величина равна 1,036. |
||||||||
5. |
Можно сделать вывод, что с помощью степенной функции мы |
||||||||
|
получаем более точное приближение. |
|
|
||||||
