
- •Министерство образования и науки российской федерации
- •Геометрия и топология
- •1. Линейные операции над векторами
- •2. Прямоугольные координаты точки и вектора. Базис
- •3. Скалярное произведение векторов
- •4.Векторное произведение векторов
- •5. Смешанное произведение векторов
- •6. Прямая на плоскости
- •7. Плоскость и прямая в пространстве
- •8. Кривые второго порядка
- •9. Полярная система координат
- •10. Поверхности
- •11. Элементы топологии
- •Список рекомендуемой литературы
3. Скалярное произведение векторов
3.1. Определить углы ∆АВС с вершинами А(2;-1;3); В(1;1;1) и С(0;0;5).
Ответ: В=С=45˚.
3.2.
Даны векторы:
 =
= +
+ +2
+2 ,
и
,
и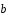 =
=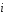 -
-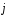 +4
+4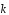 .
Определить
.
Определить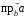 и
и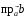 .
.
Ответ:
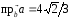 .
.
3.3.
Даны компланарные векторы ,
, ,
, ,
причем |
,
причем |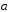 |=3,
|
|=3,
|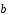 |=2,
|
|=2,
|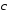 |=5,
(
|=5,
( )=60˚
и (
)=60˚
и (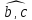 )=60˚.
Построить вектор
)=60˚.
Построить вектор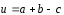 и вычислить его модуль по формулеи=
и вычислить его модуль по формулеи=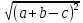
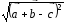 .
.
Ответ: 7.
3.4.
Определить длины диагоналей параллелограмма,
построенного на векторах:
 и
и ,
где
,
где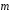 и
и – единичные векторы, угол между которыми
60˚.
– единичные векторы, угол между которыми
60˚.
Ответ:
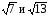 .
.
3.5.
Вычислить длину диагоналей параллелограмма,
построенного на векторах
 ,
,
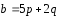 ,
если известно, что |
,
если известно, что |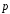 |=2
|=2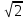 ,|
,|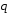 |=3 и
|=3 и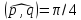 .
.
Ответ:
15,
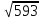 .
.
3.6.
Дан вектор
 ,
где
,
где
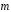 и
и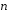 – единичные векторы с углом 120˚ между
ними. Найтиcos
– единичные векторы с углом 120˚ между
ними. Найтиcos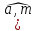 )
и cos
)
и cos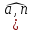 ).
).
Ответ:
cos )
)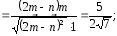 cos
cos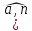 )
)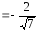 .
.
3.7.
Найти угол между векторами:
 и
и
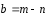 ,
где
,
где и
и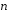 – единичные векторы, образующие угол
120˚.
– единичные векторы, образующие угол
120˚.
Ответ: 120˚.
3.8.
Определить угол между векторами
 и
и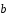 ,
если известно, что
,
если известно, что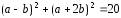 и |
и |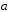 |=1,
|
|=1,
| |=2.
|=2.
Ответ: 2π/3.
3.9. Найти косинус угла φ между диагоналями (АС) и (ВD) параллелограмма, если заданы три его вершины А(2;1;3), В(5;2;-1) и С(-3;3;-3).
Ответ:

 .
.
3.10.
Даны
точки А(2;2)
и В(5;-2).
На оси абсцисс найти такую точку М,
чтобы
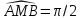 .
.
Ответ: М1(1;0) и М2(6;0).
3.11.
Даны
векторы
 (1;1)
и
(1;1)
и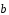 (1;-1).
Найти косинус угла между векторами
(1;-1).
Найти косинус угла между векторами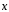 и
и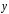 ,
удовлетворяющими системе уравнений
,
удовлетворяющими системе уравнений ,
,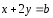 .
.
Ответ: -4/5.
3.12.
| |=3,
|
|=3,
|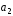 |=5.
Определить, при каком значении α векторы
|=5.
Определить, при каком значении α векторы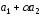 и
и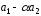 будут перпендикулярны.
будут перпендикулярны.
Ответ: α=±3/5.
3.13.
Даны векторы:
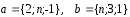 .
При каких значенияхn
угол между векторами
.
При каких значенияхn
угол между векторами
 тупой, прямой, острый?
тупой, прямой, острый?
Ответ:
n< ;n=
;n= ;n>
;n> .
.
3.14.
В треугольнике АВС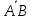 =
=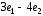 ,
,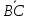 =
=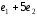 .
Вычислить длину его высоты
.
Вычислить длину его высоты ,
если известно, что
,
если известно, что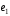 и
и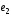 – взаимно перпендикулярные орты.
– взаимно перпендикулярные орты.
Ответ: 19/5.
3.15.
Вычислить пр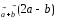 ,
если |
,
если |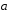 |=|
|=| |=1
и
|=1
и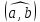 =120o.
=120o.
Ответ: 1/2.
3.16.
Зная,
что | |=3,
|
|=3,
|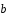 |=1,
|
|=1,
|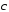 |=4
и
|=4
и =0,
вычислить
=0,
вычислить .
.
Ответ: -13.
3.17.
Векторы
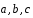 имеют равные длины и образуют попарно
равные углы. Найти координаты вектора
имеют равные длины и образуют попарно
равные углы. Найти координаты вектора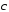 ,
если
,
если ,
,
 .
.
3.18.
Найти
координаты вектора
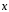 ,
коллинеарного вектору
,
коллинеарного вектору (2;1;-1)
и удовлетворяющего условию
(2;1;-1)
и удовлетворяющего условию
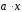 =3.
=3.
Ответ: (1;1/2;-1/2).
3.19.
Вектор
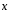 перпендикулярен векторам
перпендикулярен векторам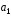 (2;3;-1)
и
(2;3;-1)
и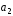 (1;-2;3)
и удовлетворяет условию
(1;-2;3)
и удовлетворяет условию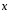
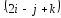 =-6.
Найти координаты
=-6.
Найти координаты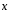 .
.
Ответ: (-3;3;3).
3.20. Квадрат разделен на три полосы одинаковой ширины и затем свернут в правильную треугольную призму. Найти угол между двумя смежными звеньями ломаной, образованной при этом диагональю квадрата.
Ответ:
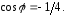
3.21.
Вычислить работу силы
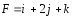 при перемещении материальной точки из
положенияА(-1;2;0)
в положение В(2;1;3).
при перемещении материальной точки из
положенияА(-1;2;0)
в положение В(2;1;3).
Ответ: 4.
3.22.
Вычислить работу силы
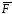 ={3;2;4},
если точка ее приложения перемещается
прямолинейно из положенияА(2;4;6)
в положение В(4;2;7).
={3;2;4},
если точка ее приложения перемещается
прямолинейно из положенияА(2;4;6)
в положение В(4;2;7).
Ответ: А=6.
3.23.
На материальную точку действуют силы
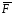 1=
1=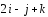 ,
, 2=
2= ,
, 3=
3= .
Найти работы равнодействующей этих сил
и силы
.
Найти работы равнодействующей этих сил
и силы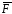 2
при перемещении точки из А(2;-1;0)
в В(4;1;-1).
2
при перемещении точки из А(2;-1;0)
в В(4;1;-1).
Ответ:1; -6.
4.Векторное произведение векторов
4.1.
|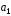 |=1,
|
|=1,
| |=2
и
|=2
и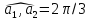 .
Вычислить:
.
Вычислить:
а)
|[ ,
,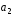 ]|;
б) |[2
]|;
б) |[2 +
+ ,
,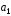 +2
+2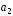 ]|;
в) |[
]|;
в) |[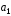 +3
+3 ,
3
,
3 -
-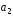 ]|.
]|.
Ответ:
а)
 ;
б) 3
;
б) 3 ;
в)10
;
в)10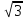 .
.
4.2. Раскрыть скобки и упростить выражения:
1)
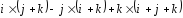 ;
;
2)
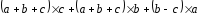 ;
;
3)
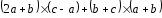 ;
;
4)
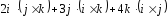 .
.
Ответ:
1)
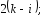 2)
2)
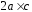 ;
3)
;
3) ;
4) 3.
;
4) 3.
4.3.Доказать,
что
 ,
и выяснить геометрическое значение
этого тождества.
,
и выяснить геометрическое значение
этого тождества.
Ответ: Площадь параллелограмма, построенного на диагоналях данного параллелограмма, вдвое больше площади данного параллелограмма.
4.4.
Векторы
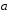 и
и составляют угол 45˚. Найти площадь
треугольника, построенного на векторах
составляют угол 45˚. Найти площадь
треугольника, построенного на векторах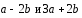 ,
если |
,
если | |=|
|=|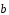 |=5.
|=5.
Ответ:
50
4.5.Дан треугольник с вершинами А(2;-1;2); В(1;2;-1); С(3;2;1). Найти его площадь.
Ответ:
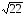 .
.
4.6. Вычислить площадь треугольника с вершинами А(1;1;1), В(2;3;4) и С(4;3;2).
Ответ:
2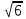 .
.
4.7. Вычислить площадь треугольника с вершинами А(7;3;4); В(1;0;6) и С(4;5;-2).
Ответ: 24,5.
4.8.
В треугольнике с вершинами А(1;-1;2),
В(5;-6;2)
и С(1;3;-1)
найти высоту h=|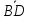 |.
|.
Ответ: 5.
4.9.Найти
площадь параллелограмма, построенного
на векторах
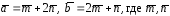 - единичные векторы с углом между ними
30.
- единичные векторы с углом между ними
30.
Ответ: 1,5.
4.10.
Вычислить площадь параллелограмма,
диагоналями которого служат векторы
2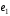 -
-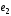 и 4
и 4 -5
-5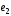 ,
где
,
где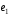 и
и – единичные векторы
– единичные векторы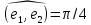 .
.
Ответ:
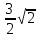 .
.
4.11.
Определить, при каких значениях α и β
вектор
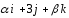 будет коллинеарен вектору[
будет коллинеарен вектору[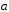 ,
, ],
если
],
если
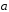 (3;-1;1),
(3;-1;1),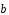 (1;2;0).
(1;2;0).
Ответ: α=-6; β=21.
4.12.
Найти координаты вектора
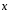 ,
если известно, что он перпендикулярен
векторам
,
если известно, что он перпендикулярен
векторам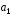 (4;-2;-3)
и
(4;-2;-3)
и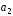 (0;1;3)
образует с ортом
(0;1;3)
образует с ортом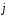 тупой угол и |
тупой угол и | |=26.
|=26.
Ответ: (-6;-24;8).
4.13.
Найти координаты вектора
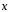 ,
если он перпендикулярен векторам
,
если он перпендикулярен векторам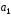 (2;-3;1)
и
(2;-3;1)
и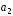 (1;-2;3),
а также удовлетворяет условию
(1;-2;3),
а также удовлетворяет условию
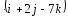 =10.
=10.
Ответ: (7;5;1).
4.14.
Сила
 приложена к точкеА(4;-2;3).
Определить момент этой силы относительно
точки О(3;2;-1).
приложена к точкеА(4;-2;3).
Определить момент этой силы относительно
точки О(3;2;-1).
Ответ:
 .
.
4.15.Сила
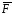 =
=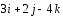 приложена в точкеМ(2;-1;1).
Найти ее момент относительно начала
координат.
приложена в точкеМ(2;-1;1).
Найти ее момент относительно начала
координат.
Ответ:
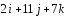 .
.
4.16.
Даны три силы:

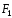 (2;-1;-3),
(2;-1;-3),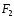 (3;2;-1)
и
(3;2;-1)
и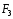 (-4;1;3),
приложенные к точкеА(-1;4;2).
Определить величину и направляющие
косинусы момента равнодействующей этих
сил относительно точки О(2;3;-1).
(-4;1;3),
приложенные к точкеА(-1;4;2).
Определить величину и направляющие
косинусы момента равнодействующей этих
сил относительно точки О(2;3;-1).
Ответ:
 ;cosα=1/
;cosα=1/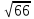 ;cosβ=-4/
;cosβ=-4/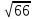 ;cosγ=-7/
;cosγ=-7/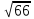 .
.
