
- •Министерство образования и науки российской федерации
- •Геометрия и топология
- •1. Линейные операции над векторами
- •2. Прямоугольные координаты точки и вектора. Базис
- •3. Скалярное произведение векторов
- •4.Векторное произведение векторов
- •5. Смешанное произведение векторов
- •6. Прямая на плоскости
- •7. Плоскость и прямая в пространстве
- •8. Кривые второго порядка
- •9. Полярная система координат
- •10. Поверхности
- •11. Элементы топологии
- •Список рекомендуемой литературы
2. Прямоугольные координаты точки и вектора. Базис
2.1.
Построить вектор
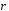 =
= =2
=2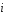 +3
+3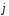 +6
+6 и определить его длину и направление
(проверить по формулеcos2α+cos2β+cos2γ=1).
и определить его длину и направление
(проверить по формулеcos2α+cos2β+cos2γ=1).
Ответ:
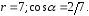
2.2.
Даны точки А(1;2;3)
и В(3;-4;6).
Построить вектор
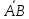 =
= ,
его проекции на оси координат и определить
длину и направление вектора. Построить
углы вектора
,
его проекции на оси координат и определить
длину и направление вектора. Построить
углы вектора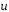 с осями координат.
с осями координат.
Ответ:
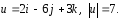
2.3.
На
плоскости хОу
даны точки А(4;2);
В(2;3)
и С(0;5)
и построены векторы
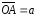 ,
, и
и .
Разложить геометрически и аналитически
вектор
.
Разложить геометрически и аналитически
вектор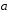 по векторам
по векторам .
.
Ответ:
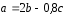 .
.
2.4.Даны три последовательные вершины параллелограмма А(1;-2;3); В(3;2;1); С(6;4;4). Найти координаты его четвертой вершины D.
Ответ: D (4;0;6).
2.5. Даны три вершины А(3;-4;7); В(-5;3;-2) и С(1;2;-3) параллелограмма ABCD. Найти его четвертую вершину D, противоположную В.
Ответ: D(9;-5;6).
2.6. Даны две смежные вершины параллелограмма А(-2;6); В(2;8) и точка пересечения его диагоналей М(2;2). Найти две другие вершины.
Ответ: С(6;-2); D(2;-4).
2.7. Определить координаты вершин треугольника, если известны середины его сторон: К(2;-4); М(6;1); N(-2;3).
Ответ: А(-6;-2); В(2;8); С(10;-6).
2.8. На оси абсцисс найти точку М, расстояние от которой до точки А(3;-3) равно 5.
Ответ: М1(7;0) и М2(-1;0).
2.9. На оси ординат найти точку М, равноудаленную от точек А(1;-4;7) и В(5;6;-5).
Ответ: М(0;1;0).
2.10. Даны вершины треугольника А(3;-1;5); В(4;2;-5) и С(-4;0;3). Найти длину медианы, проведенной из вершины А.
Ответ: 7.
2.11. Отрезок с концами в точках А(3;-2) и В(6;4) разделен на три равные части. Найти координаты точек деления.
Ответ: (4;0) и (5;2).
2.12. Определить координаты концов отрезка, который точками С(2;0;2) и D(5;-2;0) разделен на три равные части.
Ответ: (-1;2;4) и (8;-4;-2).
2.13. Треугольник задан координатами своих вершин А(3;-2;1); В(3;1;5); С(4;0;3). Вычислить расстояние от начала координат до точки пересечения медиан этого треугольника.
Ответ:
 .
.
2.14.
Задан
тетраэдр OABC.
В базисе из ребер
 и
и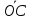 ,
найти координаты:
,
найти координаты:
а)
вектора
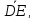 гдеD
и Е
– середины ребер
гдеD
и Е
– середины ребер
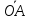 и
и ;
;
б)
вектора
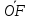 ,
гдеF
– точка пересечения медиан основания
АВС.
,
гдеF
– точка пересечения медиан основания
АВС.
Ответ: а) (-1/2;1/2;1/2); б) (1/3;1/3;1/3).
2.15.
В
тетраэдре ОАВС
медиана AL
грани АВС
делится точкой М
в отношении
 .
Найти координаты вектора
.
Найти координаты вектора в базисе из ребер
в базисе из ребер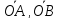 и
и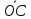 .
.
Ответ: (7/10;3/20;3/20).
2.16.
Вне
плоскости параллелограмма ABCD
взята точка О.
В базисе из векторов
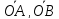 и
и найти координаты:
найти координаты:
а)
вектора
 ,
гдеМ
– точка пересечения диагоналей
параллелограмма;
,
гдеМ
– точка пересечения диагоналей
параллелограмма;
б)
вектора
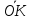 ,
гдеК
– середина стороны AD.
,
гдеК
– середина стороны AD.
Ответ: а) (1/2;0;1/2); б) (1;-1/2;1/2).
2.17.
В трапеции ABCD
известно отношение длин оснований:
 .
Найти координаты вектора
.
Найти координаты вектора
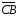 в базисе из векторов
в базисе из векторов .
.
Ответ: (1;-1/;-1).
2.18.
На плоскости заданы векторы
 (-1;2),
(-1;2),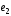 (2;1)
и
(2;1)
и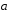 (0;-2).
Убедиться, что β=(
(0;-2).
Убедиться, что β=(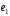 ,
,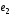 )
– базис в множестве всех векторов на
плоскости. Построить заданные векторы
и найти разложение вектора
)
– базис в множестве всех векторов на
плоскости. Построить заданные векторы
и найти разложение вектора по базису β.
по базису β.
Ответ:
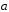 =-
=-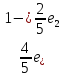 .
.
2.19.
Показать,
что тройка векторов
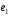 (1;0;0),
(1;0;0),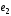 (1;1;0)
и
(1;1;0)
и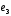 (1;1;1)
образует базис в множестве всех векторов
пространства. Вычислить координаты
вектора
(1;1;1)
образует базис в множестве всех векторов
пространства. Вычислить координаты
вектора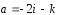 в
базисе β=(
в
базисе β=( ,
,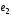
 )
и написать соответствующее разложение
по базису.
)
и написать соответствующее разложение
по базису.
Ответ:
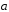 =-2е1+е2-е3.
=-2е1+е2-е3.
2.20.
Заданы
векторы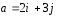 ,
,
 ,
,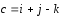 .
Найти:
.
Найти:
а)
координаты орта
 ;
;
б)
координаты вектора
 ;
;
в)
разложение вектора
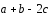 по базису β=(
по базису β=( );
);
г)
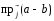 .
.
Ответ:
а) а0(2/ ;3/
;3/ ;0);
б)а-
;0);
б)а-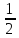 b+c=d(3;11/2;0);
в) a+b-2c=-2j;
г) прj(a-b)=6.
b+c=d(3;11/2;0);
в) a+b-2c=-2j;
г) прj(a-b)=6.
2.21.
Найти координаты орта
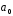 ,
если
,
если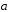 (6;7;-6).
(6;7;-6).
Ответ: (6/11;7/11;-6/11).
2.22.
Найти Z(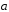 ),
если Х(
),
если Х( )=3,
Y(
)=3,
Y(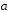 )=-9
и |
)=-9
и |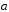 |=12.
|=12.
Ответ:
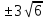 .
.
2.23.
Найти длину и направляющие косинусы
вектора
 ,
если
,
если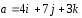 ,
, ,
,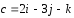 .
.
Ответ:
|p|=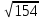 ,cosα=9/
,cosα=9/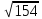 ,cosβ=8/
,cosβ=8/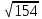 ,cosγ=3/
,cosγ=3/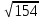 .
.
2.24.Даны
векторы
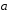 ={3;-2;1},
={3;-2;1},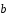 ={-2;4;-3}.
Найти длину и направление вектора
={-2;4;-3}.
Найти длину и направление вектора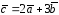 .
.
Ответ:
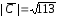 .
.
2.25.
Найти
вектор
 ,
коллинеарный вектору
,
коллинеарный вектору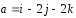 ,
образующий с ортом
,
образующий с ортом острый
угол и имеющий длину |
острый
угол и имеющий длину | |=15.
|=15.
Ответ: х=-5i+10j+10k.
2.26.
Найти вектор
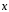 ,
образующий со всеми тремя базисными
ортами равные острые углы, если |
,
образующий со всеми тремя базисными
ортами равные острые углы, если | |=
|= .
.
Ответ: х=2i+2j+2k.
2.27.
Найти
вектор
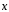 ,
образующий с ортом
,
образующий с ортом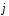 угол 60о,
с ортом
угол 60о,
с ортом
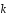 –
угол 120о,
если |
–
угол 120о,
если | |=
|=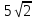 .
.
Ответ:
х=±5i+ j-
j-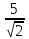 k.
k.
2.28.
При
каких значениях α и β векторы
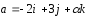 и
и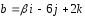 коллинеарны?
коллинеарны?
Ответ: α=-1, β=4.
