
- •Министерство образования и науки российской федерации
- •Геометрия и топология
- •1. Линейные операции над векторами
- •2. Прямоугольные координаты точки и вектора. Базис
- •3. Скалярное произведение векторов
- •4.Векторное произведение векторов
- •5. Смешанное произведение векторов
- •6. Прямая на плоскости
- •7. Плоскость и прямая в пространстве
- •8. Кривые второго порядка
- •9. Полярная система координат
- •10. Поверхности
- •11. Элементы топологии
- •Список рекомендуемой литературы


Министерство образования и науки российской федерации
Брянский государственный технический университет

УТВЕРЖДАЮ
Ректор университета
____________ О.Н. Федонин
« » ____________ 2014 г.
Геометрия и топология
Задачи к практическим занятиям для студентов I курса
очной формы обучения по направлению подготовки 010500 «Математическое обеспечение и администрирование информационных систем»
Брянск 2014
УДК 511
Геометрия и топология [Текст]+[Электронный вариант]: задачи к практическим занятиям для студентов I курса очной формы обучения по направлению подготовки 010500 «Математическое обеспечение и администрирование информационных систем». − Брянск: БГТУ, 2014. − 38с.
Разработали: В.М. Кобзев, ст. преп.
Н.В. Сычева, канд. пед. наук, доц.
Рекомендовано кафедрой Высшая математика БГТУ
(протокол №10 от 4.06.14)
1. Линейные операции над векторами

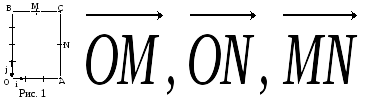
1.3.
На трех компланарных векторах
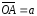 ,
,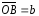 и
и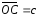 построен параллелепипед. Указать те
вектор-диагонали, которые соответственно
равны
построен параллелепипед. Указать те
вектор-диагонали, которые соответственно
равны ,
, ,
,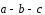 ,
и
,
и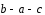 .
.
1.4.
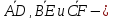 медианы треугольника АВС.
Доказать равенство
медианы треугольника АВС.
Доказать равенство
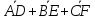 =0.
=0.
1.5.
 медианы
треугольника АВС.
Выразить через
медианы
треугольника АВС.
Выразить через
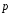 =
= и
и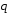 =
= векторы
векторы .
.
Ответ:
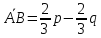 ;
;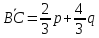 ;
;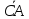 =
=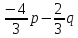 .
.
1.6.
В параллелограмме ABCDобозначены:
 =
=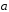 ,
,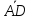 =
=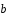 .
Выразить через
.
Выразить через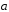 и
и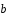 векторы
векторы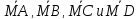 ,
где М – точка пересечения диагоналей
параллелограмма.
,
где М – точка пересечения диагоналей
параллелограмма.
Ответ:
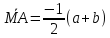 ;
;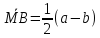 ;
;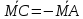 ;
;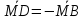 .
.
1.7.
В
треугольнике АВС .
Полагая,
.
Полагая,
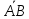 =
=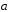 ,
,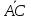 =
=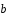 ,
выразить
,
выразить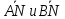 через векторы
через векторы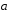 и
и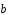 .
.
Ответ:
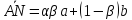 ;
;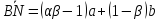 .
.
1.8.
ABCDEF
– правильный шестиугольник, причем
 =
= ,
, =
=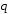 .
Выразить через
.
Выразить через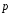 и
и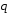 векторы
векторы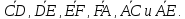
Ответ:
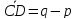 ;
;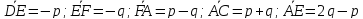 .
.
1.9.
М
– точка пересечения медиан треугольника
АВС,
О
– произвольная точка пространства.
Доказать равенство
 .
.
1.10.
В
пространстве заданы треугольники АВС
и A'B'C';
M
и M'–точки
пересечения их медиан. Выразить вектор
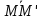 через векторы
через векторы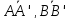 и
и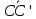 .
.
Ответ:
 ).
).
1.11.
Точки Е
и F
– середины сторон ADи
BC
четырехугольника АВСD.
Доказать, что
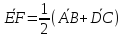 .
Ввести отсюда теорему о средней линии
трапеции.
.
Ввести отсюда теорему о средней линии
трапеции.
1.12.
В трапеции ABCD
отношение длины основания AD
к длине основания BC
равно .
Полагая
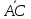 =
= ,
,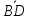 =
= ,
выразить через
,
выразить через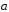 и
и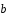 векторы
векторы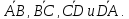
Ответ:
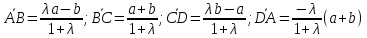 .
.
1.13.
В равнобедренной трапеции ОАСВ
угол ВОА=60˚,
ОВ=ВС=СА=2,
М
и N
– середины сторон ВС
и АС.
Выразить векторы
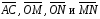

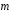 и
и –
единичные векторы направлений
–
единичные векторы направлений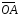 и
и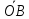
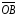
Ответ:
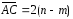 ,
,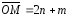 ,
,
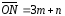 ,
,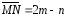 .
.
1.14.
На
стороне [AD]
параллелограмма АВСD
отложен вектор
 длины
|
длины
| |=1/5|
|=1/5|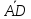 |,
а на диагонали [AC]
– вектор
|,
а на диагонали [AC]
– вектор
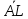 длины
|
длины
| |=1/6|
|=1/6| |.
Доказать, что векторы
|.
Доказать, что векторы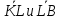 коллинеарны
и найти
такое, что
коллинеарны
и найти
такое, что
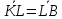 .
.
Ответ: =5.
1.15.
Разложить
вектор
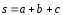 по
трем некомпланарным векторам:
по
трем некомпланарным векторам: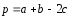 ,
,
 ,
,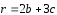 .
.
Ответ:
s=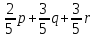 .
.
1.16.
Найти
линейную зависимость между данными
четырьмя некомпланарными векторами:
 ,
,
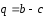 ,
,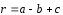 ,
,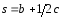 .
.
Ответ: 3p-4q-3r-2s=0.
1.17.
Даны
четыре вектора
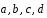 .
Вычислить их сумму, если известно, что
.
Вычислить их сумму, если известно, что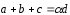 ,
,
 и векторы
и векторы
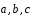 некомпланарны.
некомпланарны.
Ответ: 0.
1.18.
Даны три некомпланарных вектора
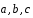 .
Доказать, что векторы
.
Доказать, что векторы
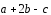 ,
, ,
,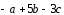 компланарны.
компланарны.
1.19.
Даны три некомпланарных вектора
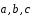 .
Вычислить значения ,
при которых векторы
.
Вычислить значения ,
при которых векторы
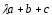 ,
,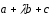 ,
,
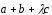 компланарны.
компланарны.
Ответ: 1,-2.
1.20.
Даны
три некомпланарных вектора
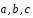 .
Вычислить значения
и µ, при которых векторы
.
Вычислить значения
и µ, при которых векторы
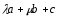 и
и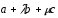 коллинеарны.
коллинеарны.
Ответ: =µ=1.
